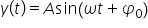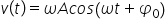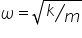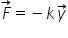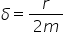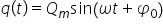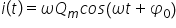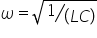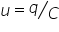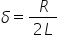Comparaţie: oscilaţii electromagnetice versus oscilaţii mecanice.

în cea de a doua Lecție despre

oscilații și unde electromagnetice

mă face o comparație între oscilațiile

electromagnetice și oscilațiile

mecanice vom vedea că deși mecanismele

ce stau la baza celor două fenomene

oscilațiile electromagnetice și

mecanice sunt diferite totuși formalismul

matematic Ce descrie ambele tipuri

de oscilații este identic odată

ce realizăm corespondența între

câteva mărimi fundamentale Haideți

să vedem acest lucru Deci ce vom

vedea în această lecție este un

tabel mai lung în care comparăm

diferite mărimi și procese ce au

loc în cele două tipuri de oscilații

pornind de la sistemul fizic ce

este folosit în descrierea ambelor

sau fiecărei tipuri de oscilație

în cazul oscilațiilor mecanice

folosim așa numitul oscilator armonic

pe când în cazul oscilațiilor electromagnetice

folosim circuitul oscilant oscilatorul

armonic este în sensul cel mai

general al cuvântului un sistem

fizic a cărei mișcări se datorează

unei forțe de tip elastic bineînțeles

cel mai Evident exemplu este un

Resort cu o constantă elastică

ca de care este atașat un corp

de masă M dar după cum am spus

în sensul cel mai general al cuvântului

dacă sistemul asupra sistemului

acționează o forță de tip elastic

adică proporțională cu elongația

atunci oscilațiile lui vor fi de

tip armonica dulci circuitului

oscilant sistemul de bază este

format din un condensator legat

la o bobină care bobină poate fi

reală și de obicei este reală în

sensul că are o rezistență neglijabilă

Deci avem un condensator cu capacitatea

c și o bobină cu inductanța l și

atunci energia inițială de pe condensator

sub forma unei tensiuni la bornele

lui se descarcă prin bobină și

aceasta dă naștere unui curent

oscilant de electroni în acest

sistem am vorbit lecția trecută

despre acest lucru primele două

mărimi și mărimile fundamentale

ce descriu oscilațiile sunt în

cazul oscilatorului armonic elongația

elongația se notează cu y punct

oarecare de pe din interiorul circuitului

oscilant de pe un conductor Spre

exemplu și ne uităm la sarcină

electrică ca funcție de timp ce

trece prin acest punct ia Fiind

dată de această ecuație observăm

că această sarcină electrică are

un un comportament oscilatia oscilează

în timp prin întrecerea a prin

punctul considerat următoarea corespondență

ce poate fi realizată imediat plecând

de la corespondență elongație sarcină

electrică este cea între viteza

25 și curentul electric viteza

de oscilație este variația elongatiei

în unitatea de timp curentul electric

este variația sarcini în unitatea

de timp și de adevăr când scriem

formulele corespondente observăm

că ele sunt identice cu excepția

faptului că amplitudinea este din

nou înlocuită cu sarcina maximă

Deci următoarea corespondență este

viteză de o și la ție curent electric

Haideți să vorbim despre pulsația

celor două sisteme oscilante în

cazul și la Tolle armonic pulsația

proprie este radical din Constanta

elastică împărțită la masă m în

cazul sistemului sau circuitului

oscilant pulsația proprie este

egală cu radical din 1 împărțit

la el orice de aici deducem că

se poate face corespondența între

Constanța elastică și inductanța

l de asemeni Mă scuzați între masă

și inductanța el și între Constanta

elastică și 1pc inversul capacități

întradevăr când am definit inductanța

Și am discutat despre ea inductanta

unei bobine se comportă într un

circuit de curent alternativ intru

în cel ce amintește de inerția

unui corp în mecanică Deci Masa

este întrun care e o proprietate

de inerție este între un circuit

de curent alternativ echivalentă

cu inductanța Deci rezultă că forța

elastică este echivalentă tensiunii

condensatorului deoarece forța

elastică este egală cu ca și respectând

corespondențele stabilite până

acum ys3d sarcinii și Constanta

elastică corespunde inversului

capacități Deci forța elastică

este echivalentul tensiunii condensatorului

iarăși gândul la procesele ce stau

la baza celor două sisteme aceasta

această corespondență are sens

pentru că mărimea sau fenomenul

ce stă la baza oscilațiilor oscilatorului

armonic este forța elastică ia

generează aceste oscilații la fel

în cazul circuitului oscilant fenomenul

sau mărimea ce stă la baza oscilațiilor

electromagnetice este tensiunea

inițială de pe condensator următoarele

proprietăți sau mărimi ce pot fi

echivalate sunt forța de inerție

cu tensiunea electromotoare indusă

deja am vorbit despre această echivalență

masa cu inductanța și impulsul

cu suc de ce forța de inerție este

prin definiție masa ori accelerația

Care este egală cu masa ori variația

vitezei la timp sănătatea de timp

egală cu variația impulsului în

unitatea de timp asta datorită

definiție impulsului camasa viteză

dar dacă ne uităm la tensiunea

electromotoare indusă Ea este egală

legea afara Denis până asta cu

inductanța mulți tool cu variația

intensității curentului în unitatea

de timp dar știm deja că inductanță

este echivalentul cu masă și curentul

electric cu viteza Deci comparând

această ecuație cu această ecuație

vedem că ele sunt echivalente asta

înseamnă că forța Care este egală

cu acest produs este echivalentul

tensiunea electromotoare indusă

Deci forța Forța este echivalentul

tensiune electromotoare in dus

sau tensiunii pe bobină de asemeni

știm că variația variația intensității

curentului este egală cu variația

fluxului împărțită la inductanță

datorită definiției inductanță

inductanța este introdusă ca coeficientul

de proporționalitate dintre flux

și intensitate comparând din nou

cu acestei ecuații observăm că

impulsul pe al unui oscilator armonic

este echivalentul fluxul continuând

putem echivala energia cinetică

cu energia magnetică și energia

potențială cu energia electrică

și folosim echivalentele deja stabilit

energia cinetică este definită

ca mv pătrat pe 2 Dar m este echivalează

cu inductanța l iar vs echivalează

cu curentul electric de ce e pătrat

pe 2 este echivalent cu el e pătrat

pe doi în concluzie energia cinetică

a1.ro și lați mecanice este echivalentă

energiei magnetice la fel elongația

este echivalată cu sarcină electrică

de ceai pot echivalent cu q pătrat

iar k este echivalent cu unul pe

Ce rezultă că energia potențială

au armonii este echivalentul cu

energia electrică a unui it oscilant

Ultimele ultimile echivalente sunt

următoarele între întreg procesul

sau idee întreaga întregul concept

de conservare a energiei în cele

două tipuri de sisteme fizice datorită

următorului Factor energia totală

în cadrul în cazul straturi armonic

este suma dintre cinetică și cea

potențială și egală cu ca a pătrat

împărțit la 2 și ea este o constantă

în cazul energiei totale a circuitului

oscilant a este egală după cum

am văzut cu suma dintre energia

magnetică și energia electrică

și egală cu sarcina maximă la pătrat

împărțită la 2c care este o constantă

constatul că energia totală este

o constantă poate fi văzut în cazul

și actorului armonic făcând derivata

energiei totale în raport cu timpul

și obținem aceste Două ecuații

care pot fi scrise aceste două

acest doi termeni a are al sumei

și acest această formulă poate

fi scrisă ca viteza muncită cu

masa accelerație plus ca orice

am folosit aici faptul că de e

urias termeni este egal cu 0 10

termen este egal cu masa ori accelerația

minus forța elastică și egal cu

0 la fel putem proceda în cazul

circuitului oscilant derivă energia

totală obținem această sumă de

doi termeni iar apoi folosind faptul

că variația sarcinii în unitatea

de timp este intensitatea obținem

intensitatea curentului muncită

cu el de la det plus qpc Dar acest

termen este și el egal cu zero

pentru că este egal cu minus cu

plus uc Care este zero va duc aminte

din legea afara de există un semn

deci putem face o echivalență directă

între întreg procesul de conservare

a energiei atât formularea lui

cât și derivat derivarea lui între

cele două sisteme și final oscilații

amortizate oscilații amortizate

apar în uși la tura armonic când

pe lângă forța elastică avem și

o forță rezistivă care este proporțională

cu viteza și destin semnul pus

sau sens opus există un coeficient

de proporționalitate r și când

rezolvăm această ecuație adică

scriem m masa ori accelerația care

e derivată de ordinul doi aruncați

y plus erori viteza carii derivată

de ordinul întâi alungați plus

ca egal cu 0 când rezolvăm obținem

după cum știm Și am discutat această

ecuație al Ungariei oscilațiilor

armonizate la fel în cadrul circul

în cazul circuitului oscilant oscilații

amortizate apar atunci când bobina

este una reală Adică are o rezistență

sau mai general vorbind avem o

rezistență în circuit și atunci

ecuația care se scrie este că suma

tensiunilor este egală cu zero

scriind explicit obținem că will

Care este el de la DT deci el derivată

de ordinul doi asasini raport cu

timpul plus r e Care este r d q

ar trebui să fie aici nu inundația

de dq la de ten plus q împărțit

la c care este usi egal cu 0 Rezolvând

iar și această ecuație diferențială

de ordinul 2 obținem această ecuație

pentru sarcină în circuitul oscilant

și din nou vedem că avem o corespondență

unul la unul între toate mărimile

ce apar în cadrul ecuațiilor ce

descriu oscilațiile amortizate

Deci avem aceeași formulă cu excepția

faptului că amplitudinea este din

nou cuser o sarcină maximă în cadru

circuitul oscilant și a 0 în cazul

cu satul de armonică apoi mărimile

caracteristice și anume pulsația

aceeași formă și ajungem la acest

coeficient de atenuare de alta

Care este dat de următoarele Două

ecuații în cazul circuitului în

cadrul circuitului oscilant este

rezistența împărțit la 2 l și în

cazul o și latură armonic coeficientul

aer al forței rezistent în părți

la două ore ma deja am făcut corespondența

m echivalentă cu el rezultă că

coeficientul aer al forței rezistive

este echivalentul rezistenței ceci

iarăși mod Evident are sens concluzie

undele electromagnetice și undele

mecanice au exact aceleași ecuații

dacă facem următoarele patru echivalente

deci tot ce trebuie să înlocuind

pentru a genera un set de un set

complet de ecuații pentru un caz

din celălalt caz este una din sau

mai multe din aceste echivalente

elongația este echivalentul sarcini

electrice masă este echivalentul

inductantei Constanta elastică

este echivalentul inversului capacității

și coeficientul forței rezistive

este echivalentul rezistenți o

mulțime sau toate celelalte ecuații

și formule pot fi deduse din acestea

Spre exemplu după cum am văzut

viteza este echivalentă cu intensitatea

curentului rezultă din prima echivalență

deoarece viteza este de e y Deci

dacă e y e q Vaillant cu q atunci

de grila de tei este echivalent

cu dq la dtd și viteza este echivalentul

intensității curent alt exemplu

să dăm impulsul este echivalent

cu fluxul aceasta rezultă din faptul

că k este echivalentul lui 1 pe

ce inversului capacității și y

este echivalentul sarcinii electrice

scuzați nu impulsiv alint cu fluxul

nu rezultă din faptul că m este

echivalent cu el și vrem este echivalent

cu e Deci Emi volent cu el și vechi

Vaillant cu e ceea ce tocmai am

stabilit asta înseamnă că mv echivalentul

lui el cu el ori adică impulsul

este echivalent cu fluxul și ceea

ce am vrut să spun înainte k este

echivalent cu 1pc și y k echivalent

cu nu PC și y q Vaillant cu q se

traduce sau rezultă în faptul că

forța elastică este echivalentă

cu tensiunea pe condensator și

așa mai departe există un șir lung

de formule ce putem deriva plecând

de la aceste patru echivalent