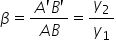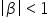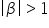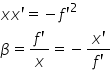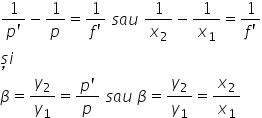Convenţia de semn. Formulele Newton şi Descartes pentru imagini în lentile.
Partajeaza in Google Classroom

Transcript
În ce dată lecții de optică geometrică
vom de duce formule lentilelor
Newton și de carte întâi să prezentăm
Convenția de semn folosită în aceste
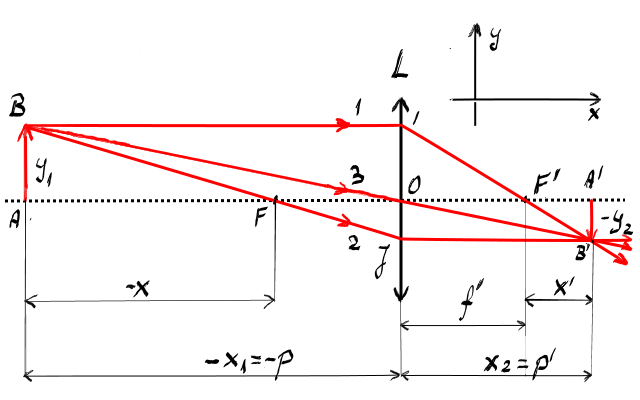
formule ceea ce vedeți este schema
formării imaginii unui obiect abm
pentru o lentilă convergentă Convenția
de semn stipulează că distanțele
sunt algebrice adica un semn plus
sau minus mai puțin distanțele
focale pentru care folosind Convenția
că distanța focală imagine exprime
este pozitivă lentile convergente
a și negativă în antilla divergente
felul în care stabilim semnul distanțelor
este următorul pentru coordonata
verticală alegem în sens pozitiv
pentru distanța obiectului pentru
înălțimea obiectului iar pentru
coordonata orizontală alegem în
sens pozitiv distanțelor care au
același sens cu cel al propagării
razelor de lumină Spre exemplu
dacă știm că obiectul are o înălțime
de să zicem 5 cm vom folosi un
un semn plus în fața acestui acestei
distanțe dacă știind că Imaginea
a prim b prim are o înălțime să
zicem de 3 cm o Vom lua cu semnul
minus pentru că a prim b prim are
sens invers obiectului abia pe
coordonată orizontală dacă știm
că obiectul se află în propoziție
o a de 10 cm față de lentilă vom
lua această distanță cu semnul
minus pentru că o a ars sensul
invers razelor de lumină dacă știm
că imaginea se află la o poziție
o aprinde să zicem 15 cm de lentilă
vom lua această distanță cu semnul
plus pentru că o a prim are același
sens ca cel al razelor de lumină
de ce procedăm așa poate părea
ca o complicație dar de fapt ea
este o mare simplificare a formulelor
pentru că cu ajutorul convenții
de semn putem de duce formule generale
veți vedea vom avea un set de formule
pentru toate cazurile particulare
ca să fiu mai specific sisar întâmplat
dacă nu am avea convex este convenții
desen Spre exemplu în acest caz
particular care îl avem în schema
noastră putem scrie că a f plus
f o este egal cu a o lună considerare
numai distanțe fără niciun semn
dacă în schimb am avea un alt caz
particular să zicem cel în care
obiectul ab ar fi între centrul
Optic al lentilei și focarul principal
imagine atunci această relație
nu ar mai fi adevărată și în loc
ar trebui să scriem af plus a o
m este egal cu F o și în felul
acesta ar trebui să le ducem câte
un set de formule pentru fiecare
caz particular și avem foarte multe
cazuri particulare de construcții
de imagini în lentile convergente
divergente diferite poziții diferite
tipuri de obiecte reale virtuale
și așa mai departe acesta este
motivul pentru care se folosește
Convenția de să continuăm acum
cu deducere a formulei altan începem
prin a introduce următorii doi
parametri f a se notează cu x și
exprimă prin să nu te Aza cu X
prin acesta și pozițiile obiectului
față de focarul principal obiect
și al imaginii față de focarul
principal imagini datorită faptului
că triunghiul ABS este asemănător
cu triunghiul o j f Deci triunghiul
a d f este asemănător cu triunghiul
o j f putem Scrie următoarele relații
de proporționalitate ab supra o
j este egal cu F a supra asko dar
oje este egal cu a prim b prim
Deci o j egal cu a prim b prim
pentru că raza reflectată cu roșu
este paralel cu Axa optică principală
și f o este egal cu asprime cu
sensul razelor de lumină Deci are
sens pozitiv Deci rezultă că a
b împărțit la a prim b prim este
egal cu x împărțit la f prim Considerând
Triunghiurile a prim D prim f prim
și o e f prim putem vedea că ele
sunt asemănătoare a prim b prim
f prim este asemănător cu o ef
prin au unghiurile egal și atunci
putem scrie relațiile de proporționalitate
a prim b prim împărțit la o e este
egal cu F prim a prim împărțit
la f prim o oi este egal cu AB
pentru că raza incidență albastră
este paralel cu Axa optică principală
și F prim o este egal cu minus
distanța focală exprim pentru care
sensul opus razelor de lumină deci
de aici putem scrie că avem împărțit
la a prim D prim am și inversat
această relație este egal cu minus
spre împărțit la exprimă din nou
sens în semnul minus apare din
exprime o care are sensul invers
razelor de lumină combinând aceste
două relații putem scrie Deci această
relație combinată cu această relație
implică că x înmulțit cu x prim
este egal cu minus exprim la pătrat
de asemeni introducând un nouă
parametru Beta în numit mărirea
liniară ca raportul dintre înălțimea
imaginii și înălțimea obiectului
putem scrie că el este egal cu
asprime împărțit la x sau minus
x prim împărțit la exprima această
formulă se numește formula Newton
și este acompaniată de o formulă
corespunzătoare pentru mărirea
liniară înainte de a trece la formula
de carte deducerea volumului de
card câteva lucruri importante
despre mărirea liniară Beta nici
din iubita este definit ca a prim
b prim împărțit la AB și în mod
Evident descrie raportul dintre
înălțimea imaginii și înălțimea
obiectului ea conține următoarele
informații importante dacă Deta
este mai mare decât 0 atunci mod
Evident imaginea este dreaptă Pentru
că asta înseamnă că avem același
semn al imaginii cu al obiectului
ceea ce înseamnă că au același
sens dacă Beta este mai mic decât
0 atunci imaginea este răsturnat
dacă modulul lui Betta este mai
mic decât 1 în mod Evident imaginea
este mai mică și dacă modulul lui
Beta este mai mare decât 1 imaginea
este mai mare Deci calculând valoarea
lui Beta putem să extragem mai
multe proprietăți ale imaginii
în raport cu obiectul să trecem
la deducerea fumul formulei de
ca vom folosi aceeași schemă ca
cea precedentă notăm o A deci poziția
a obiectului cupe și o aprind nici
poziția imaginii Cum pe primul
atunci putem scrie că x care reamintesc
prin definiție este sa am este
egal cu f m plus o a reamintesc
când scriem aceste relații folosind
distanțe algebrice indicele conțin
un semn fără acest semn în mod
Evident în cazul scheme precedent
această relație nu ar fi adevărată
ia devine adevărată incluzând semnele
care este egal cu F prim plus pe
pentru xprimm care reamintesc este
definit ca f prim a din nou algebric
Deci conține semn este egal cu
F prim om plus o a prim același
comentariu toate distanțele conținut
semn și numai așa relațiile devină
adevărate ținând cont de semnul
lor care egal în continuare cu
minus f prim plus pe prima și deci
putem folosi relația Newton pentru
a scrie că x mulți cu exprimă din
această aceste ecuații va fi egal
cu F prin plus pe înmulțit cu minus
f prim plus pe prim și egal din
relația Newton pricină demonstrată
mai devreme Cum minus exprim la
pătrat această ultimă egalitate
este relația Newton deci putem
deduce de aici că a minus pe Ifrim
plus pe prim f prim plus pe pe
prim egal Cuza am rezolvat această
înmulțire și apoi am scris explicit
ultima egalitate în această formă
împărțind această ecuație prind
pe exprim pe prim obținem că 1
împărțit la b prim minus 1 supra
b este egal cu 1 pe Ifrim această
ecuații se numește relația de card
și Deci relația sau formula de
cald și este acompaniată cu o formulă
pentru mărirea liniară care din
nou e definită ca a a prim b prim
împărțit la avem și care este egal
în contextul noilor parametri pe
și pe prim cu raportul dintre pe
prim și pe