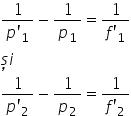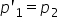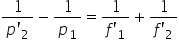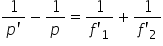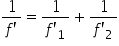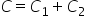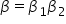Exemplu de calcul al lentilelor. Sisteme de lentile centrate şi acolate.

încet da Șase lecții de optică

geometrică vom da un exemplu de

folosire a formulelor lentilelor

Newton și de card pe care îl am

de dus în lecția cincea și apoi

vom discuta despre sistemele de

lentile să aplicăm acum aceste

formule pentru a descrie imaginea

formată între anumit caz particular

Deci cazul este cel prezentat în

această schemă în care obiectul

are înălțimea H egal cu 2 cm distanța

focală a lentilei convergente a

este 10 cm și poziția obiectului

față de lentilă o a este 30 de

cm dorim să aflăm proprietățile

imagini folosim formula de card

care spune că 1 supra pe prim minus

1 supra b este egal cu 1 supra

f prim Cum scriem explicit și asta

înseamnă că 1 supra pe prim minus

1 supra pe care este minus 30 de

centimetri pentru că o a are sensul

invers razelor de lumină este egal

cu 1 supra 10 Rezolvând pentru

pe prim această ecuație obținem

către prim este egal cu plus 15

cm calculăm și mărirea liniară

în acest caz Deci peta este egal

cu p prim împărțit la p este egal

cu plus 15 împărțit la minus 30

și Deci Veta este egal cu minus

0 imediat din aceste valori putem

deduce următoarele lucruri despre

imagini că este răsturnată deoarece

Veta este mai mic decât 0 că este

mai mică deoarece modul de Beta

este mai mic decât 1 și că este

reală deoarece pe prim este mai

mare decât 0 Să considerăm un alt

caz dacă o a este egal cu 8 cm

asta înseamnă că a mutat obiectul

între centrul Optic și focarul

principal obiect la fel introducem

în formula de card și obținem 1

supra pe prim minus 1 supra minus

8 este egal cu 1 pe 10 rezultă

că pe prim este egal cu minus 40

de centimetri iar Beta este egal

cu minus 40 împărțit la minus 8

este egal cu plus 5 deci pe prinde

vine negativ iar Beta de vine pozitiv

proprietățile imaginii Ce rezultă

din acești parametri este că este

dreaptă asta pentru că bataie mai

mare decât 0 mai mare pentru că

modul din Betta este mai mare decât

unul și virtuală pentru că pe prim

este mai mic decât 0 în sfârșit

un ultim caz cel în care o a este

egal cu 15 cm ce se întâmplă în

acest caz obiectul este dincolo

de dublul distanței nu scuzați

obiectul este între distanța focală

și dublul distanței focale Deci

intre 10 și 20 de cm în acest caz

avem 1 supra pe prim a minus 1

supra minus 15 cm este egal cu

1 pe 10 Rezolvând pentru pe prim

obținem o valoare de plus 30 de

centimetri și rezolvăm Pentru Betta

care va fi plus 30 împărțit la

minus 15 obținem o valoare de minus

2 pentru aceste două valori ale

celor doi parametri obținem următoarele

proprietăți ale imaginii este răsturnată

pentru că b d mai mic decât 0 este

mai mare pentru că modul din Beta

este mai mare decât 1 și este reală

pentru că pe prim este mai mare

decât 0 din aceste trei exemple

calculate cu o singură schema putem

vedea puterea convenției desen

cu o singură formulă formula de

carte aceasta am rezolvat trei

cazuri diferite obținând toate

proprietățile imaginii din semnul

și evaluarea parametrilor rezultați

instrumentele optice moderne folosesc

de obicei mai multe lentile aranjate

în varii sisteme de lentile în

aceste sisteme imaginea primei

lentile este obiect pentru cea

de a doua lentilă și așa mai departe

adică imaginea ce lentilei an devine

obiect pentru lentila n plus 1

sistemele de lentile subțiri cu

Axa optică comună se numesc sisteme

centrate sistemele de lentile subțiri

lipite se numesc sistem acolate

și au centrul Optic comun în această

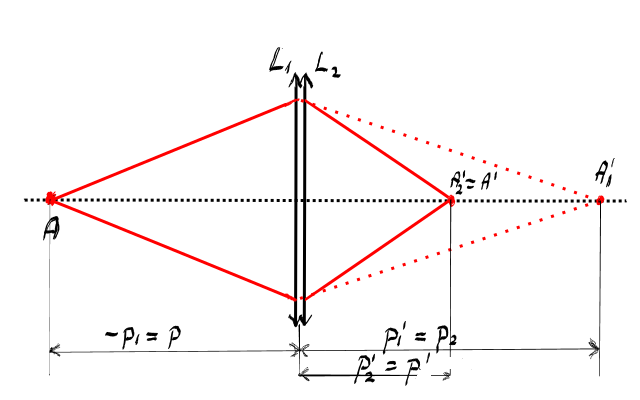
schemă avem un sistem de două lentile

convergente a l1 L2 care sunt centrate

pentru că au aceeași axa optică

principală și acolate pentru că

sunt lipite Considerând un obiect

aflat în poziția a vom obține o

imagine în antivirus în poziția

A1 după cum am spus imaginea primele

zile de vin obiect pentru cea de

a doua și de 5-a de a doua lentila

obținem o imagine a prim a obiectului

A1 a prim Este evident imaginea

finală a sistemului de lentile

dacă notăm cu p poziția obiectului

cupe 1 poziția primei imagini și

cu pe primul poziția celei de a

doua imagini putem scrie relațiile

de card pentru cele două lentile

și anume 1 supra pe 1 minus 1 supra

b este egal cu 1 supra F1 prim

unde e 1 prim este distanța focală

a primei lentile și egal în continuare

cu convergența primei lentile în

cea de a doua lentilă putem scrie

că 1 supra pe prim minus 1 supra

pe 1 este egal cu 1 supra F2 prim

care este egal cu convergența celei

de a doua lentile F2 prime este

distanța focală a lentilei L2 adunând

acestei două relații obținem că

unul supra pe prim minus 1 supra

b este egal cu 1 supra F1 prim

plus 1 supra F2 prim și egal mai

departe Cu ce unu plus C2 observăm

că în stânga primului semn de egalitate

avem relația tipică de carte Adică

1 supra pozitia imaginii pe prim

fiind poziției imaginii întregului

sistem de lentile minus 1 supra

p unde p este poziția obiectului

întregului sistem de lentile egal

cu o anumită valoare dacă această

valoare o notăm cu meci dacă notăm

1 supra F1 prim plus 1 supra F2

prim cu 1 supra f prim atunci acest

f prim este distanța focală a întregului

sistem de lentile și în continuare

obținem o relație similară pentru

convergență și anume că suma convergență

lor lentilelor este egală cu convergența

a sistemului de lentile cu această

notație și definiție obținem o

relație o formulă de card Standard

pentru sistemul de lentile centrate

și acolate Adică 1 supra pe prim

minus 1 supra b este egal cu 1

supra f prim mai mult decât atâta

dacă ne uităm la magnifica rea

mă la mărirea liniară a întregului

sistem ia va fi egală cu B prim

supra p m care poate fi scris ca

pe 1 supra p m înmulțit Cum pe

prim supra pe unul dar pe unul

supra pe este Betta 1 și pe prim

supra pe 1 este beată 2 măririle

liniare ale celor două lentile

rezultă că mărirea liniara sistemului

de centile centrat și acolat este

produsul măririlor liniare ale

lentilelor componente după cum

am spus acest tip de sisteme de

lentile cu Axa optică comună și

eventual și acolade este foarte

utilizat în sistemele optice moderne

a Spre exemplu vedeți aici o imagine

cu lentilele din Obiectivul unei

camere foto putem vedea o colecție

de multe lentile care au axa optică

comună