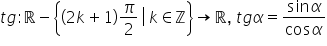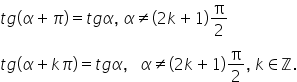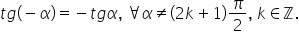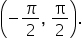Funcția tangentă
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să discutăm
despre funcția tangentă și proprietățile
acesteia avem cercul trigonometric
și am construit o tangentă la cerc
aceasta intersectează cercul în
punctul A am prelungit raza vectoare
om care intersectează tangenta
în punctul b de coordonate 1 Y8
sau punctului b este 1 de mare
c proiecția acestui punct pe axa
o x este punctul A iar lungimea
segmentului o a este egală cu unu
de o are c o a este rază În cercul
unitate proiecția punctului b pe
axa o y reprezintă ordonat acestui
punct și am notată cu Y8 servim
așa dutcus a format un triunghi
dreptunghic oab iar în acest triunghi
dreptunghic putem să aplicăm relația
trigonometrică tangentă tangenta
este raportul dintre cateta opusă
și cateta alăturată unghiul Alfa
Așadar o să avem AB supra o A dar
lungimea segmentului AB este egală
cu Y8 bisect mentului o a este
1 prin urmare tangentă de Alfa
este egală cu Y8 servim Așadar
că putem să construim o funcție
care Asociază fiecărui unghi Alfa
ordonata punctului de pe tangentă
iar această funcție va fi funcția
tangentă Haide să exprimăm și sinus
de Alfa ținuți este raportul dintre
cateta opusă și ipotenuză Deci
avem AB supra OB iar cosinus de
Alfa este Cat alăturată supra ipotenuză
o a supra o b și acum se face raportul
dintre sinus și cosinus și vom
avea a b supra o b supra o a supra
ab egal cu ab supra OB ori o b
supra o a se simplifică o b cu
o beșină rămâne ab supra o ei dar
ab supra o a este chiar tangentă
de Alfa observăm Așadar că tangenta
unghiului Alfa este raportul dintre
sinus și cosinus prin urmare funcția
tangentă nu va fi definită pentru
acele valori ale lui Alfa pentru
că are cosinusul este 0 iar cu
sinus de Alfa este 0 când Alfa
este pi pe 2 3 pi pe 2 5 pe 2 și
așa mai departe Deci cosinus ia
valoarea 0 pentru orice m titlu
impar de pisu Predoi prin urmare
funcția tangentă va fi definită
pe R din care scoate m la cele
valori care anulează numitorul
aceste fracții de ce avem multipli
impari de pi supra 2 și cu valori
în R Unde k este un număr întreg
și acum Haideți să vedem semnul
aceste funcții pentru unghiuri
din cele patru cadrane am văzut
că tangenta unghiului Alfa este
lungimea segmentului AB de pe tangentă
dacă segmentul ab este situat deasupra
axei o x atunci tangenta este pozitivă
iar dacă segmentul a b este situat
sub axa o x atunci tangenta va
fi negativă în cazul în care Alfa
este un unghi din primul cadran
atunci observăm că tangenta este
pozitivă cu cât unghiul crește
spre p supra 2 atunci lungimea
acestui segment crește și se apropie
de plus infinit îmi spune că tangentă
de pi supra 2 este plus infinit
cu alte cuvinte tangenta nu are
o valoare reală în pi supra 2 observăm
că în acest caz raza vectoare este
paralelă cu tangenta așa dar nu
există punct de intersecție între
rază și tangentă de aceea mă spune
că tangenta nu este definită în
pi supra 2 dacă unghiul Alfa crește
spre pi supra 2 atunci tangenta
este plus infinit iar dacă unghiul
Alfa a scade de la P spre supra
2 atunci tangenta va fi minus infinit
observăm că în acest caz segmentul
roz este situat sub axa o x aici
avem minus infinit iar Aici plus
infinit cu alte cuvinte în jurul
valorii de p supra 2 tangenta sa
rad de la plus infinit la minus
infinit acum pentru umple din al
doilea cadran din intervalul pi
supra 2 pi tangenta este negativă
observăm că acest segment Rosie
este situat sub axa o x pentru
unghiurile din al treilea cadran
tangenta este pozitivă și aici
am prelungit raza vectoare până
intersectează tangenta în punctul
b iar pentru unghiurile situate
în al patrulea cadran tangenta
este negativă în continuare să
discutăm câteva aspecte despre
monotonia acestei funcții pentru
unghiurile din primul cadran Deci
când Alpha aia valori cuprinse
în intervalul 0 pi supra 2 funcția
este crescătoare observăm că cu
cât crește măsura unghiului cu
atât crește și lungimea segmentului
AB în p supra 2 tangenta nu este
definită pentru unghiurile din
cadranul 2 funcția este crescătoare
îmi spune că tangenta crește de
la minus infinit spre zero pentru
unghiurile din cadranul 3 tangenta
este de asemenea crescătoare observăm
că cu cât crește măsura unghiului
Alfa cu atât crește și lungimea
segmentului AB în 3 piept 2 tangenta
nu este definită iar pentru unghiurile
din cadranul 4 tangenta este crescătoare
aceasta crește de la minus infinit
spre zero ne interesează în continuare
și paritatea acestei funcții pentru
aceasta voi construi un unghi negativ
acesta este unghiul minus Alfa
tangenta este dată de lungimea
acestui segment observăm că tangentă
de minus Alfa va fi egal cu minus
tangentă de Alfa pentru că aici
segmentul este orientat în sens
negativ prin urmare vom spune că
tangenta este o funcție impară
și acum să discutăm câteva aspecte
despre periodicitate aceste funcții
funcția tangentă este o funcție
periodică dacă la acest unghi Alfa
adunăm pai atunci se obține acest
unghi Deci aici avem unghiul Alfa
plus pai prin urmare tangenta unghiului
Alfa are aceeași valoare cu tangenta
unghiului Alfa plus pentru că vorbim
de același segment AB punctul de
este o funcție periodică iar perioada
principală este pi așa dar este
suficient să studiem funcția tangentă
pe un interval de lungime a unei
perioade Iar acest interval va
fi minus pi supra 2 pi supra 2
Aici este minus pi supra 2 coincide
cu punctul 3 pi pe 2 Pe cercul
trigonometric deoarece deplasând
un de la zero în sens negativ un
sfert de cerc ajungem în acest
punct prin urmare graficul funcției
tangentă va fi reprezentat pe intervalul
minus pi supra 2 pi supra 2 și
apoi va fi translatat la stânga
și la dreapta de a lungul axei
o x Haideți să vedem graficul acestei
funcții acesta este în graficul
funcției tangentă observăm că este
suficient să trasăm graficul acestei
funcții pe un interval de lungimea
unei perioade Iar acest interval
este minus pi supra 2 supra 2 observăm
că tangentă de zero este zero funcția
este impară prin urmare graficul
va fi Simetric față de origine
și observăm de asemenea că funcția
este crescătoare pe intervale de
formă supra 2 pi supra 2