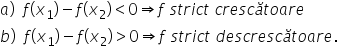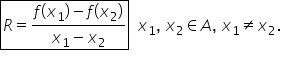Funcții monotone (aplicații)
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să facem câteva
exerciții în care 100 de ani monotonia
unor funcții și începe cu această
funcție f definită pe r cu valori
in r f de x egal cu minus 3x plus
5 alegem două valori arbitrare
din domeniul de definiție fie X1
X2 numere reale astfel încât x
1 să fie mai mic decât x 2 m Calculați
diferență e de x 1 minus x 2 obținem
minus 3x 1 plus 5 minus minus 3x
2 plus 5 egal cu minus 3 x 1 plus
3x 2 factor comun pe minus 3 pe
lângă x 1 minus x 2 x 1 este mai
mic decât x 2 înseamnă că această
diferență este negativă iar cu
minus 3 din față acest produs devine
pozitiv prin urmare f de x 1 este
mai mare decât f de x 2 ia din
moment ce e funcția f schimbă relația
de ordine dintre argumente pentru
valorile funcției înseamnă că aceasta
este o funcție strict descrescătoare
continuăm cu al doilea exercițiu
avem funcția f definită pe r cu
valori in r f de x egal cu x plus
2 daca x este mai mic sau egal
decât minus 3 și x plus 5 dacă
x este mai mare decât minus 3 în
cazul în care avem o astfel de
funcții definite pe ramuri vom
studia 3 cazuri în primul caz alegem
cele două valori X1 X2 din primul
interval mai exact din intervalul
minus infinit minus 3 apoi alegem
cele două valori din intervalul
minus 3 plus infinit și în al treilea
ca azi alegem X1 din primul interval
și X2 din al doilea interval dacă
funcția f va avea aceeași monotonie
vom putea să stabilim monotonia
pe întreg domeniul de definiție
r Așadar începem cu primul că azi
alegem X1 X2 din intervalul minus
infinit minus 3 astfel încât x
1 să fie mai mic decât x 2 calculăm
diferența fdx 1 minus f de x 2
x 1 plus 2 minus x 2 plus 2 obținem
x 1 minus x 2 Dacă x-1 este mai
mic decât x noi această diferență
este negativă prin urmare f de
x 1 este mai mic decât f de x 2
observăm că funcția f păstrează
relația de ordine dintre argumente
și pentru valorile funcției Așadar
funcția f este strict crescătoare
pe acest interval minus infinit
minus 3 în al doilea caz om consideră
X1 X2 din intervalul minus 3 infinit
astfel încât x 1 să fie mai mic
decât x 2 m Stabiliți semnul diferenței
f de x 1 minus f de x 2 x 1 plus
5 minus x 2 plus 5 egal cu x 1
minus x 2 această diferență este
negativă pentru că x 1 este mai
mic decât x 2 prin urmare f este
strict crescătoare pe intervalul
minus 3 infinit și în al treilea
cos mult considera x 1 mai mic
sau egal decât minus 3 și x 2 mai
mare strict decât minus 3 Haideți
să adunăm la Prima in ecuație numărul
2 și obținem x 1 plus 2 mai mic
sau egal decât minus 1 dar x 1
plus 2 este f de x 1 mai mic sau
egal decât minus 1 la a doua inegalitate
adunăm numărul 5 și avem X2 plus
5 mai mare strict decât 2 prin
urmare a f de x 2 va fi strict
mai mare decât 2 dacă f de x este
mai mic sau egal decât minus 1
și f de x 2 este mai mare strict
decât doi putem trage concluzia
că fdx 1 este mai mic decât f de
x 2 prin urmare funcția f este
strict crescătoare pe întreg domeniul
de definiție iar următorul exercițiu
avem funcția f definită pe r cu
valori in r f de x egal cu x la
a treia plus 7 x plus 2 vă spuneam
în filmul precedent că există două
metode prin care putem să studiem
monotonia funcțiilor iar a doua
metodă presupune stabilirea semnului
raportului de variație asociat
funcției f Haide să aplicăm această
metodă pentru acest exercițiu alegem
Așadar două valori x 1 x 2 din
domeniul de definiție astfel încât
x 1 să fie mai mic decât x 2 și
vom calcula raportul f de x 1 minus
f de x 2 supra x 1 minus x 2 obținem
X1 la a treia plus 7 x 1 plus 2
minus x 2 la a treia minus 7 x
2 minus 2 totul supra X1 minus
X2 se reduce 2 cu minus noi avem
X1 la a treia minus X2 la a treia
plus 7 pe lângă x 1 minus x 2 supra
x 1 minus x 2 din descompunerea
această diferență X1 la a treia
minus x 2 la a treia în factori
folosind următoarea formulă a la
a treia minus de la a treia este
egal cu a minus b pe lângă a pătrat
plus ab plus de pătrat aceasta
este formula prin care putem Să
descompunem în factori diferența
cuburilor a două numere reale dacă
nu Știați această formulă o stii
si acum Prin urmare avem la numărător
x 1 minus x 2 pe lângă x 1 la pătrat
plus x 1 x 2 plus X2 la pătrat
plus 7 pe lângă x 1 minus x 2 supra
x 1 minus x 2 acum la numărător
dăm factor comun pe x 1 minus x
2 și simplificăm cu expresia de
la numitor în final obținem X1
la pătrat plus X1 X2 plus X2 la
pătrat plus 7 și acum ar trebui
să vedem Ce semn are această expresie
în forma în care este scrisă acum
nu putem să stabilim semnul ei
Așadar vom încerca să rescriem
această expresie ca un pătrat perfect
sau ca o sumă de pătrate perfecte
observăm că avem aici X1 la pătrat
și X2 la pătrat prin urmare ne
putem gândi la următoarea formula
de calcul prescurtat a plus b totul
la pătrat este egal cu a la a doua
plus doi a b plus b la a doua observăm
că cele două relații se aseamănă
puțin însă în această formulă avem
factorul 2 din fața produsului
ab iar Aici lipsește acest Factor
prin urmare pentru a putea restrânge
această sumă folosind această formulă
de calcul prescurtat ar trebui
ca unul dintre acești termeni X1
sau X2 să aibă numitorul 2 pentru
că având numitorul 2 în momentul
în care efectuând produsul 2 ab
adică 2 x 1 x 2 se simplifică 2
și aici rămâne X1 X2 Așadar vom
scrie suma primilor trei termeni
astfel x 1 pe 2 plus x 2 totul
la pătrat și acum să vedem dacă
trebuie să mai adunăm sau să scădem
niște termeni Haideți să calculăm
aceeași sumă x 1 pe 2 plus x 2
totul la pătrat obținem X1 la a
doua pe 4 plus 2x 1 pe 2 x 2 plus
X2 la pătrat se simplifică doi
cu doi aceasta era și ideea rămâne
X1 X2 cum avem și aici X2 la pătrat
este ok Ca și mai sus însă aici
avem X1 la a doua pe 4 iar în expresia
inițială aveam X1 la pătrat asta
înseamnă că trebuie să mai adunăm
termenul 3 x 1 la pătrat supra
4 pentru că adunând X1 la pătrat
pe 4 cu 3 X1 la pătrat pe 4 obținem
4 x 1 la pătrat pe 4 se simplifică
4 și în final ne rămâne X1 la a
doua Deci exact ce avem aici Așadar
aici mai trebuie să adunăm trei
X1 la pătrat pe patru și mai avem
acel 7 Ați înțeles ceva bun să
continuăm atunci aici avem un pătrat
perfect deci acest număr este pozitiv
aici avem X1 la pătrat prin urmare
și acest termeni este pozitiv la
care se mai adună și numărul 7
prin urmare toată această expresie
va fi strict pozitivă asta înseamnă
că este mai mare decât 0 Deci raportul
de variație a funcției este pozitiv
prin urmare funcția f este strict
crescătoare și un ultim exercițiu
avem funcția f definită pe intervalul
închis minus 36 cu valori in r
f de x egal cu 2 plus x pătrat
alegem două valori arbitrare X1
X2 din intervalul minus 36 astfel
încât x 1 să fie mai mic decât
x 2 să calculăm f de x 1 minus
f de x 2 mm 2 plus X1 la pătrat
minus 2 minus X2 la pătrat și obținem
X1 la pătrat minus X2 la pătrat
acum descompunem în factori x 1
minus x 2 pe lângă x 1 plus x 2
știind că x 1 minus x 2 este negativ
pentru că x 1 este mai mic decât
x 2 însă nu putem preciza semnul
acestei sume x 1 plus x 2 Pentru
că X1 și X2 pot să fie numere atât
pozitive cât și negative Așadar
nu putem să stabilim monotonia
funcției pe întreg domeniul de
definiție pe intervalul minus 36
Și atunci vom lua restricția aceste
funcții la intervalul minus 3 0
și apoi la intervalul 06 Așadar
nu stabilim monotonia funcției
pe intervale de monotonie în primul
caz vom considera X1 și X2 din
intervalul minus 3 0 astfel încât
x 1 să fie strict mai mic decât
x 2 în acest caz numerele x 1 și
2 sunt negative sau X2 ar putea
fi și zero însă Oricum este mult
mai ușor să stabilim semnul acestei
sume așa dar e de x 1 minus f de
x 2 este egal cu x 1 minus x 2
pe lângă x 1 plus x 2 această diferență
este negativă și suma x 1 plus
x 2 este negativă iar dacă X2 ar
fi 0 x 1 fiind negativ atunci această
sumă este negativă produsul este
pozitiv Așadar f de x 1 este mai
mare decât f de x 2 din moment
ce funcție f schimbă relația de
ordine dintre argumente pentru
valorile înseamnă că f este strict
descrescătoare pe intervalul minus
trei zero să vedem ce se întâmplă
în cazul în care x 1 x 2 aparțin
intervalului 0 6 astfel încât x
1 să fie mai mic decât x 2x 1 minus
fdx 2 este egal quixx 1 minus x
2 pe lângă x 1 plus x 2 diferența
Rămâne în continuare negativă însă
X1 X2 sunt numere pozitive așa
dar această sumă este pozitivă
produsul final va fi negativ De
ce de x 1 este mai mic decât f
de x doi de aici putem să tragem
concluzia că funcția f este strict
crescătoare pe intervalul 0 6 Așadar
să reținem că atunci când nu putem
stabili monotonia funcției pe întreg
domeniul de definiție am studiat
monotonia funcției pe intervale
de monotonie

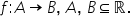
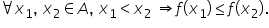
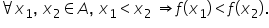
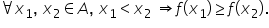
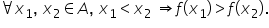
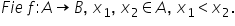
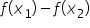 și o comparăm cu zero:
și o comparăm cu zero: