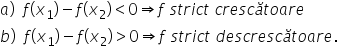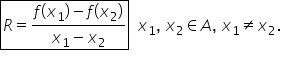Funcții monotone (teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
o categorie importantă de funcții
este cea a funcțiilor monotone
despre care să discutăm în acest
clip avem o funcție f definită
pe a cu valori în b nu îmi spune
că f este crescătoare dacă oricare
ar fi X1 și X2 două elemente ale
se arbitrat din domeniul de definiție
între care există relația x 1 mai
mic decât x 2 să avem că f de x
1 mai mic sau egal decât f de x
2 observăm că o funcție este crescătoare
dacă ia păstrează relația de ordine
dintre argumente și pentru valorile
funcției în cazul în care aici
avem o inegalitate strictă atunci
funcția se numește strict crescătoare
să dăm și un exemplu și F definită
pe r cu valori în intervalul 0
infinit f de x egal cu 2 la x alegem
două elemente X1 și X2 din R astfel
încât x 1 să fie mai mai decât
x noi în acest caz observăm că
2 la puterea x 1 este mai mic decât
2 la puterea X2 prin urmare f de
x 1 va fi mai mic decât f de x
doi Așadar spunem în acest caz
că funcția f este strict crescătoare
o funcție este numește descrescătoare
dacă oricare ar fi X1 și X2 elemente
arbitrare din domeniul de definiție
între care există relația x 1 mai
mic decât x 2 să avem că fdx 1
mai mare sau egal decât f de x
2 Așadar o funcție descrescătoare
schimbă relația de ordine dintre
argumente pentru valorile funcției
în cazul în care aici avem inegalitate
strictă vom spune că funcția este
strict descrescătoare să dăm și
un exemplu și e f definită pe 0
infinit cu valori în intervalul
0 infinit f de x egal cu 1 pe x
dacă alegem două elemente X1 și
X2 din domeniul de definiție astfel
încât x 1 să fie mai mic decât
x 2 atunci 1 supra X1 va fi mai
mare decât 1 supra X2 dintre două
fracții cu același numărător este
mai mare cea cu numitorul mai mic
prin urmare f de x 1 este mai mare
decât f de x 2 în acest caz funcția
este strict descrescătoare o funcție
se numește monotonă dacă este crescătoare
sau descrescătoare să vedem în
continuare cum ar arăta graficele
acestor funcții considerăm un sistem
de axe x o y alegem pe axa absciselor
două elemente x 1 x 2 astfel încât
x 1 să fie mai mic decât x 2 ne
interesează să vedem cum ar arăta
graficul unei funcții crescătoare
în cazul în care f este crescătoare
Atunci e de x 1 trebuie să fie
mai mic decât f de x 2 pe axa ordonatelor
avem valorile funcție pentru argumentele
X1 și X2 Haideți să notăm mai simplu
aceste valori cu igrec 1 și cu
y 2 dacă funcția este crescătoare
atunci y 2 trebuie să fie mai mare
decât y cu nu așa dar pe axa ordonatelor
y2 trebuie să fie situat mai sus
decât y 1 și acum dacă unim cele
două puncte printr o dreaptă obținem
graficul unei funcții crescătoare
dacă citim acest grafic de la stânga
spre dreapta observăm că acesta
urcă să vedem cum arată graficul
în cazul în care funcția este descrescătoare
avem sistemul de axe x o y pe axa
absciselor alegem arbitrar două
valori x-1 și x 2 astfel încât
x 1 să fie mai mic decât x 2 dacă
funcția este strict descrescătoare
atunci f de x 1 este mai mare decât
f de x 2 pe axa ordonatelor avem
valorile acestei funcții pentru
argumentele X1 și X2 undeva aici
am avea efd X1 sau mai simplu y1
iar E F d x 2 sau y2 trebuie să
fie mai mic decât y cu nu așa dar
pe axa ordonatelor y2 este situat
mai jos decât igrec 1 iar acum
dacă unim aceste două puncte printre
o dreaptă obținem graficul unei
funcții descrescătoare observăm
că acest grafic citit de la stânga
spre dreapta coboară prin urmare
putem să stabilim monotonia unei
funcții și Privind graficul acesteia
dacă graficul urcă atunci funcția
este crescătoare iar dacă graficul
coboară atunci funcția este descrescătoare
există însă și situații în care
graficul unei funcții poate arăta
Cam așa observăm că pe această
porțiune graficul funcției urcă
Deci funcția este crescătoare apoi
pe această porțiune graficul coboară
apoi graficul urcă Deci funcția
este crescătoare și pe ultima porțiune
graficul coboară Deci funcția este
descrescătoare observăm Așadar
că este posibil ca o funcție să
nu aibă aceeași monotonie pe întreg
domeniul de definiție și atunci
îmi spune că ea are intervale de
monotonie Iată pe acest interval
funcția este crescătoare pe acest
interval funcția este descrescătoare
pe următorul interval funcția este
crescătoare iar pe ultimul interval
funcția este descrescătoare Așadar
să reținem că în cazul în care
funcția nu are aceeași monotonie
pe întreg domeniul de Definiție
si va studia monotonia acesteia
pe intervale să vedem în continuare
care sunt modalitățile prin care
putem studia monotonia unei funcții
în rezolvarea exercițiilor exista
doua procedee prin care putem să
dea monotonia unei funcții fie
f definită pe a cu valori în b
și alegem două elemente X1 X2 arbitrare
din domeniul de definiție astfel
încât x 1 să fie mai mic decât
x 2 în prin procedeul prin care
putem studia monotonia unei funcții
este să calculăm diferența f de
x 1 minus f de x 2 și Avem două
situații posibile dacă f de x 1
minus f de x 2 este mai mic decât
0 asta înseamnă că f de x 1 este
mai mic strict decât ix2 în acest
caz funcția f este strict crescătoare
și a doua posibilitate dacă f de
x 1 minus f de x 2 este mai mare
decât zero Adică mtx 1 este mai
mare decât f de x 2 atunci în această
situație funcția este strict descrescătoare
și un al doilea procedeu prin care
putem studia monotonia funcțiilor
alegem două valori arbitrare X1
și X2 din a astfel încât x 1 să
fie mai mic decât x 2 calculăm
valoarea raportului fdx 1 minus
f de x 2 supra x 1 minus x 2 acest
raport se mai numește raportul
de variație asociat funcției f
Avem două cazuri posibile Dacă
raportul este pozitiv atunci funcția
este strict crescătoare iar și
explicația dacă x-1 este mai mic
decât x 2 atunci această diferență
este negativă Dacă raportul este
pozitiv atunci diferența de la
numărătorul fracției trebuie să
fie și aceasta negativă prin urmare
fdx 1 este mai mic decât f de x
2 și atunci funcția este strict
crescătoare și a doua posibilitate
Dacă raportul este negativ atunci
funcția va fi strict descrescătoare
în această situație diferența x
1 y minus x 2 rămâne negativă Dar
pentru că raportul este negativ
diferența de la numărător este
pozitivă Așadar fdx 1 este mai
mare decât f de x 2 prin urmare
funcția este strict descrescătoare
în rezolvarea exercițiilor o să
ne alegem una dintre cele două
modalități de a studia monotonia
funcțiilor Iar acest lucru se va
întâmpla în clipul urmator

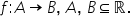
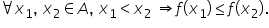
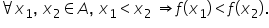
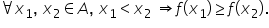
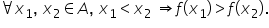
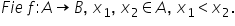
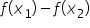 și o comparăm cu zero:
și o comparăm cu zero: