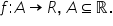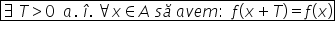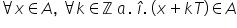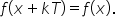Funcții periodice
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție discutăm despre
funcții periodice și pornind de
la acest exemplu avem fracția 134
supra 999 Dacă transformăm această
fracție ordinară în fracție zecimală
obținem 0 34 în perioadă avem Așadar
o fracție zecimală periodică simplă
Haideți acum să definim o funcție
f definită pe mulțimea numerelor
naturale nenule cu valori în n
unde f de n este a n a zecimală
a acestui număr 134 supra 999 și
acum să calculăm câteva valori
pentru această funcție f de 1 este
prima zecimală a numărului Adică
1 f de 2 a doua zecimală este 3
a treia zecimală este 4 a patra
zecimală este 1 pentru că urmează
din nou perioada 134 a cincea zecimală
este 3 așa se zice mulla este patru
dacă ne uităm cu atenție la valorile
aceste funcții observăm că acestea
se repetă din 3 în 3 Iată Prin
urmare avem următoarea egalitate
este de 1 este egal cu F de 4 apoi
e f de 2 este egal cu F de 5 iar
E F de 3 este egal cu F de 6 și
așa mai departe SDN a fi egal cu
F d n plus 3 Iată oricare ar fi
n număr natural nenul observăm
Așadar că valorile funcției se
repetă din 3 in 3 iar o astfel
de funcție se numește funcție periodică
Iar acest număr 3 se numește perioadă
mai exact perioadă principală iar
perioada se notează în general
cu litera t mare și acum să ne
uităm puțin love Rafi cu la aceste
funcții fiind o funcție f definită
pe n cu valori în n pe axa absciselor
avem numere naturale iar pe axa
ordonatelor avem valorile acestor
numere prin funcția f avem Așadar
un punct al graficului punctul
de coordonate 1 1 apoi de 2 este
3 f de 3 este 4 s de 4 este 1 pe
5 este 3 f de 6 este 4 și așa mai
departe Așadar graficul acestei
funcții este dat de mulțimea punctelor
roșii din reperul cartezian dacă
ne uităm cu atenție la graficul
acestei funcții observăm că ar
fi fost suficient să trasăm graficul
pe un interval de lungime a unei
perioade iar generale lui pe tot
domeniul de definiție să se facă
translate în duel la dreapta dea
lungul axa absciselor am evidențiat
în culori diferite acea porțiune
a graficului care se repetă în
cazul acestei exemplu perioada
este 3 așa Dar ar fi fost suficient
să Reprezentăm doar prima porțiune
a graficului apoi se translată
În graficul de a lungul axei absciselor
Aceasta este o proprietate importantă
a graficului funcțiilor periodice
și acum să dăm și definiția acestor
funcții avem Așadar următoarea
definiție și o funcție definită
pe a cu valori in R unde a este
o submulțime a lui R Nu spune că
funcția este numește periodică
dacă există un număr pozitiv te
astfel încât pentru orice x din
a să aibă loc egalitatea f de x
egal cu f de x plus 3 atâta timp
cât și valoarea x plus te rămâne
în domeniul de definiție numărul
3 se numește perioadă iar dacă
există o cea mai mică perioadă
atunci aceasta se va numi perioadă
principală și se notează de obicei
cute 0 să vedem în continuare o
proprietate a funcțiilor periodice
dacă ai fi este periodică înseamnă
că are loc această egalitate din
definiție e f de x egal cu f de
x plus 3 normare Dacă la argumentul
funcției x adunăm perioada te funcția
va avea aceeași valoare înseamnă
că la acest argument x plus 3 Putem
să mai adunăm încă o dată perioada
t iar funcția va avea aceeași valoare
așa dar putem să scriem egal mai
departe cu f d x plus t plaste
Dar acest lucru este egal cu f
de x plus 2 t și acum putem să
adunăm încă o dată perioada t și
obțin aceeași valoare pentru funcția
f decedat în continuare cu f de
x plus 3 t și așa mai departe însă
această primă egalitate se poate
scrie și invers d x plus p este
egal cu fdx Așadar dacă din argumentul
funcției scădem perioada te funcția
va avea aceeași valoare Deci Putem
intra la mai departe cu f d x minus
t din argumentul x am scăzut perioada
te așa cum am făcut aici la primul
pas mai departe putem să scădem
încă o dată perioada 3 iar funcția
și a păstra valoarea Deci avem
f de x minus 2 t și așa mai departe
m d x minus trei puncte puncte
prin urmare să reținem că dacă
o funcție este periodică atunci
pentru 8cx din domeniul de definiție
și pentru orice număr k întreg
are loc egalitatea f de x egal
cu f de x plus kt am văzut că numărul
k poate să fie atât pozitiv cât
și negativ prin urmare pentru orice
k întreg are loc această egalitate
în continuare o să facem un exercițiu
și e f definită pe mulțimea numerelor
naturale nenule cu valori în n
f de n este egal cu ultima cifră
a numărului 3 la puterea n Arătați
că f este periodică și Aflați perioada
principală de 0 din moment ce f
de n este egal cu ultima cifră
a numărului 3 la puterea n Haide
să scriem câteva puteri ale numărului
3 la n 3 la unuia este trei trei
la a doua nouă trei la 327 trei
la 481 3 la a cincea 243 3 la 6:00
729 trei la 7:00 2187 și trei la
a opta 6561 Bineînțeles că pe noi
ne interesează doar ultima cifră
Iată Avem 3 9 7 1 3 9 7 1 și așa
mai departe f de 1 este ultima
cifră a numărului 3 la puterea
întâia adică 3 de 2 este ultima
cifră a numărului 3 la a doua 9
f de 3 este ultima cifră a numărului
3 la a treia adică 7 f de 4 este
ultima cifră a numărului 3 la a
patra Adică 1 de 5 este 3 de 6
este 9 este de 7 este 7 și F de
8 este 1 observăm că valorile acestei
funcții se repetă din 4 în 4 pentru
că f de 1 este egal cu EF de 5
Iată 3 și 3 apoi e f de 2 este
egal cu F de 6 fete de 3 este egal
cu F de 7 chef de 4 este egal cu
EF de 8 și așa mai departe observăm
că e f de n este egal cu F de n
plus 4 oricare ar fi n număr natural
nenul prin urmare perioada principală
a acestei funcții este patru de
0 egal cu patru Haideți să demonstrăm
acest lucru și pe cazul general
Dacă n este un număr de forma 4
k avem f de 4 k egal ultima cifră
a numărului 3 la puterea 4 k egal
cu ultima cifră a numărului 3 la
a patra totul la puterea k dar
ultima cifră a numărului 3 la a
patra este unu și ridicat la o
putere ca apa obținem 1 Apoi dacă
este de forma aa 4K plus 1 funcția
va fi ultima cifră a numărului
3 la puterea a 4 k plus unu care
se mai poate scrie 3 la puterea
4K ori 3 la a întâia 3 la puterea
4K are ultima cifra egală cu unu
care înmulțit cu 3 ne va da trei
dacă argumentul funcției este de
forma a 4 k plus 2 atunci avem
ultima cifră a numărului 3 la 4K
plus 2 Care este egal cu ultima
cifră a lui 3 la 4K ori 3 la a
doua ultima cifră a lui 3 la 4
k este 1 înmulțit cu 9 9 iar dacă
argumentul funcției este de forma
a 4 k plus 3 avem ultima cifră
a numărului 3 la 4K plus 3 egal
cu ultima cifră a lui 3 la 4K ori
3 la a treia 3 la a treia este
27 de cm cifră a acestui număr
este șapte iar ultima cifră a numărului
3 la 4 k este 1 în final obținem
177 iar dacă argumentul funcției
ar fi de forma 4K plus 4 atunci
acest caz se reduce la primul în
care se obține ultima cifră a numărului
egală cu unu am arătat astfel că
funcția este periodică iar perioada
principală este egală cu 4