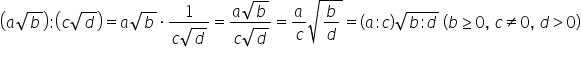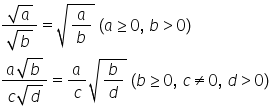Împărțirea numerelor reale

în această lecție voi prezenta

împărțirea numerelor reale de formă

a radical din b dacă x este un

număr real nenul atunci inversul

lui x este numărul 1 supra x întotdeauna

are loc următoarea relație x înmulțit

cu 1 pe x este egal cu 1 supra

x ori x și egale cu unu așa dar

atunci când înmulțim un număr cu

inversul său Rezultatul este întotdeauna

1 de exemplu Inversul numărului

radical din 2 va fi 1 supra radical

din 2 sau Inversul numărului 3

radical din 7 va fi 1 supra 3 radical

din 7 să vedem în continuare Cum

împărțim doi radicali dacă avem

de exemplu radical din x împărțit

la radical din x y atunci vom înmulțit

de împărțitul cu inversul împărțitorului

Așadar vom avea radical din x înmulțit

cu 1 radical din y egal în continuare

cu radical din x supra radical

din y în această expresie se mai

poate scrie radical din x supra

y dacă avem de exemplu numere de

formă a radical din x împărțit

la b radical din Y5 vom înmulțim

primul număr a radical din x cu

inversul celui de al doilea ori

1 supra b radical din x y se poate

scrie sub formă de fracție are

de cal din x supra b radical din

y în continuare cu a supra b înmulțit

cu radical din x supra y aceste

relații au loc atâta timp cât numerele

de sub radical sunt mai mari sau

egal cu 0 Deci x trebuie să fie

mai mare sau egal cu 0 y trebuie

să fie strict mai mare ca zero

întrucât acesta apare și ca numitor

al fracției iar numărul b trebuie

să fie diferit de 0 să rezolvăm

în continuare câteva exerciții

un prim exercițiu avem radical

din 90 împărțit la radical din

10 așa cum spuneam mai devreme

înmulțim deîmpărțitul radical din

90 cu inversul împărțitorului ori

1 supra radical din 10 egal în

continuare cu radical din 90 supra

10 egal radical din 90 egal cu

3 un al doilea exercițiu minus

radical din 20 împărțit la radical

din 5 minus radical din 20 ori

1 supra radical din 5 egal aplicăm

regula semnelor și avem minus radical

din 20 supra 5 egal minus radical

din 4 și egal cu minus doi al treilea

exercițiul 6 radical din 10 supra

2 radical din 5 această fracție

se poate scrie astfel 6 supra 2

înmulțit cu radical din 10 supra

5 6 supra 2 este 3 radical din

10 pe 5 este radical din 2 în alt

exercițiu minus 8 radical din 50

împărțit la minus 4 radical din

2 putem să scrie sub formă de fracție

sau putem calcula direct minus

8 împărțit la minus 4 este 2 iar

radical din 50 împărțit la radical

din 2 este radical din 25 egal

în continuare cu 2 ori 5 și egal

cu 10 și un ultim exercițiu 5 9

radical din 14 împărțit la 3 radical

din 7 și aici Am calculat direct

9 împărțit la 3 este 3 iar radical

din 14 împărțit la radical din

șapte este radical din 2