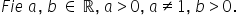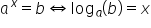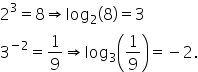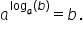Logaritmi (introducere)
Tag-uri
Partajeaza in Google Classroom

Transcript
logaritmi au foarte multe aplicații
de exemplu pe H unei soluții se
calculează folosind logaritmul
zecimal sau nivelul unui sunet
în decibeli se exprimă prin dulong
Aron a raportului dintre două intensități
iar dacă Privim o lumină strălucirea
pe care o percepem eu expresia
logaritmului emisie de energie
de asemenea magnitudinea unui cutremur
corespunde logaritmului amplitudinii
undelor seismice descompunerea
radioactivă este un alt domeniu
în care întâlnim logaritm cu ajutorul
acestora se poate calcula durata
persistenței radioactivității unor
elemente în continuare o să vedem
ce sunt logaritmi dacă avem următoarea
ecuație 2 la puterea x egal cu
8 aceasta se mai poate scrie a
astfel 2 la x este egal cu 2 la
a treia se observă foarte ușor
că x este egal cu trei dacă avem
ecuația 5 la puterea x egal cu
1 supra 25 atunci aceasta se poate
scrie 5 la x este egal cu 5 la
puterea minus 2 de unde rezultă
că x este egal cu minus 2 dacă
însă avem o ecuație de forma aceasta
2 la x egal cu 7 atunci răspunsul
nu mai este atât de Evident iar
pentru rezolvarea acesteia necesară
introducerea noțiunii de logaritm
soluția acestei ecuații x va fi
logaritmul în baza 2 a lui 7 cu
alte cuvinte x este exponentul
la care se ridică baza 2 pentru
a obține valoarea 7 Deci cuvântul
logaritm este un alt termen folosit
pentru exponentul unei puteri în
celelalte două cazuri putem scrie
că 3 este logaritmul în baza 2
a lui 8 sau minus doi este logaritmul
în baza 5 a numărului 1 supra 25
în general dacă a la x este egal
cu b atunci vom spune că x este
logaritmul în baza a numărului
b Deci logaritmul este Puterea
la care trebuie să ridicăm pe a
pentru a obține numărul b e foarte
importantă acum să vedem ce fel
de număr poate să fie a respectiv
b mă pune condiția ca ei să fie
număr strict pozitiv a diferit
de 1 iar b trebuie să fie de asemenea
strict pozitiv si o sa vedem imediat
de ce mai întâi să vedem de ce
bază nu poate să fie egală cu 0
dar pe baza ar fi 0 și aș dori
de exemplu să rezolve ecuația logaritm
în baza 0 din 3 egal cu x atunci
această relație ar conduce la următoarea
zero la puterea x egal cu 3 sau
dacă avem logaritm în baza 0 din
7 egal cu x obținem relația 0 la
x egal cu 7 ori aceste Două ecuații
nu au soluții pentru că numărul
0 ridicat la orice putere este
egal cu 0 Deci nu există niciun
număr real x astfel încât 0 la
x să fie egal cu 3 sau 0 la x să
fie egal cu 7 din acest motiv baza
logaritmului adică numărul ei nu
poate lua valoarea 0 să vedem acum
de ce baza trebuie să fie diferită
de 1 dacă bază ar fi 1 și am avea
de exemplu următoarea ecuație logaritm
în bază unul din 3 egal cu x aceasta
ar conduce la relația 1 ridicat
la puterea x egal cu 3 sau logaritm
în baza 1 din 7 egal cu x ar conduce
la relația 1 la x egal cu 7 dam
din nou aceste Două ecuații nu
au soluții pentru că numărul 1
ridicat la orice putere este egal
cu 1 așa dar nu există niciun număr
real X care să satisfacă relația
unul la x egal cu 3 sau 1 la x
egal cu 7 din acest motiv se pune
condiția ca baza logaritmului să
fie diferită de 1 am văzut până
acum că baza logaritmului trebuie
să fie diferită de 0 și diferită
de 1 să vedem acum de ce trebuie
pusă condiția ca bază să fie număr
strict pozitiv dacă bază ar fi
negativă și aș vrea de exemplu
să rezolve ecuația aceasta logaritm
în baza minus 3 din y1 pe 4 am
luat Așadar o bază negativă minus
3 pentru a obține pe y2 scrie relația
yii2 minus 3 la puterea 1 pe 4
avem Așadar un număr negativ ridicat
la o putere rațională aceasta va
conduce la radical de ordinul 4
din minus 3 în să știm că nu există
radical de ordin parte din tul
număr negativ din acest motiv baza
logaritmului nu poate să fie număr
negativ Așadar să reținem că întotdeauna
baza logaritmului este număr strict
pozitiv și diferit de 1 în continuare
Vrem să vedem de ce numărul b trebuie
să fie și acesta strict pozitiv
b se mai numește și argumentul
logaritmului să încercăm să găsim
un număr pozitiv care ridicat la
o putere să dea o valoare negativă
e bine o să Observați că acest
lucru va fi imposibil de exemplu
dacă avem numărul pozitiv 2 pe
care îl ridicăm la exponentul 3
Evident Rezultatul este 8 Deci
strict pozitiv dacă avem de exemplu
2 la minus 3 rezultatul va fi 1
supra 2 la a treia adică unul pe
8 dar și unul pe 8 este număr pozitiv
Dacă aș calcula de exemplu 2 la
puterea 1 pe 3 obținem radical
de ordinul 3 din 2 dar și acesta
este pozitiv Am putea să încercăm
de exemplu 2 la puterea 0 Da Rezultatul
este 1 Așadar pozitiv în consecință
observăm că nu există nici un număr
pozitiv care ridicat la o putere
să dea o valoare negativă așa dar
atâta timp cât bază este număr
strict pozitiv atunci și argumentul
logaritmului adică numărul b va
fi strict pozitiv pornind de la
egalitatea a la x egal cu b și
punând în locul lui X logaritm
în bază a din b se obține următoarea
relație care va fi utilă în rezolvarea
unor exerciții a la logaritm în
baza a din b este egal cu b De
ce am înlocuit în această egalitate
pe x cu logaritm în bază a din
b De exemplu dacă avem trei la
puterea logaritm în bază 3 din
5 promo obține 5 în cazul în care
baza logaritmului este 10 logaritmul
se va numi logaritm zecimal și
se notează cu l g iar în cazul
în care baza logaritmului este
numărul a este o constantă matematică
aproximativ egală cu 2 este un număr
irațional atunci logaritmul în
baza e se numește logaritm natural
și se notează cu l n în clipul
următor o să discutăm despre proprietățile
logaritmilor