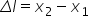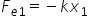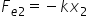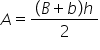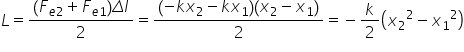Lucrul mecanic. Forţe conservative. Cazuri particulare de lucru mecanic.
Tag-uri
Partajeaza in Google Classroom

Transcript
în prima lecție despre legi de
conservare în mecanică vom vorbi
despre noțiunile de lucru mecanic
și forțe conservativ noțiunea de
lucru mecanic este foarte aproape
de sensul al întâlnit în viața
de zi cu zi al cuvântului lucru
Sau dacă doriți muncă sau efort
ea implică un om sau mașină ce
acționează asupra unui corp cu
o forță f pentru a provoca o anumită
deplasare a corpului pe care o
notăm cu d Deci definiția lucrului
mecanic este următoarea lucrul
mecanic efectuat de o forță constantă
Asupra unui corp este produsul
dintre modulul forței și distanța
parcursă de corp pe direcția și
în sensul forței ca urmare a acțiunii
iei câteva comentarii în legătură
cu această definiție dar înainte
să dăm ecuația lucrul mecanice
rezultă din această definiție Deci
lucrul mecanic este produsul dintre
forță și deplasarea de produse
de acea forță comentariile sunt
următoare le lucrul mecanic este
definit în aici pentru o forță
constantă bineînțeles va exista
un lucru mecanic și el pentru forțe
ce variază în timp sau cu deplasarea
vom vorbi despre acest caz puțin
mai târziu si la comentariu se
referă la partea subliniată partea
a doua subliniat în această definiție
și anume că deplasarea de trebuie
să fie în sensul forței F sau viceversa
forța s trebuie să fie în sensul
deplasării altfel lucrul mecanic
va fi 0 ce vreau să spun cu asta
Spre exemplu dacă avem o altă forță
F2 ce acționează asupra aceluiași
corp deși corpul se deplasează
lucrul mecanic al forței F2 este
egal cu 0 pentru că această forță
F2 fiind perpendiculară pe deplasare
a corpului nu a fi putut produce
această deplasare corpul se deplasează
dar cauza deplasării trebuie să
fie alta în cazul acesta forță
aer în consecință lucrul mecanic
al forței F2 este 0 iar nu produce
o deplasare în general fără deplasare
nu există lucrul mecanic Spre exemplu
dacă împingeți un ca numai de forță
dar peretele nu se mișcă nu ați
efectuat un lucru mecanic pe altă
consecință după cum se vede din
acest desen dacă forță este perpendiculară
pe deplasare lucrul mecanic este
zero în general forțele sunt de
două tipuri din punctul de vedere
al consecințelor lor putem avea
forțe motoare precum Forța F în
acest desen care sunt forțele Ce
produc deplasarea putem de asemenea
avea forțe rezistente precum o
forță de frecare Deci dacă corpul
și nostru și suprafața pe care
se află au o forță de frecare ce
acționează între ele atunci forța
de frecare este forța rezistentă
a se opune deplasării lucrul mecanic
al forței motoare se numește lucrul
mecanic motor și este luat cu semn
pozitiv lucrul mecanic al unei
forțe rezistente precum forța de
frecare în cazul nostru este se
numește lucrul mecanic rezistent
și este luat cu semne dativ Deci
lucrul mecanic al forței f În cazul
nostru este pozitiv și lucrul mecanic
al forței de frecare este negativ
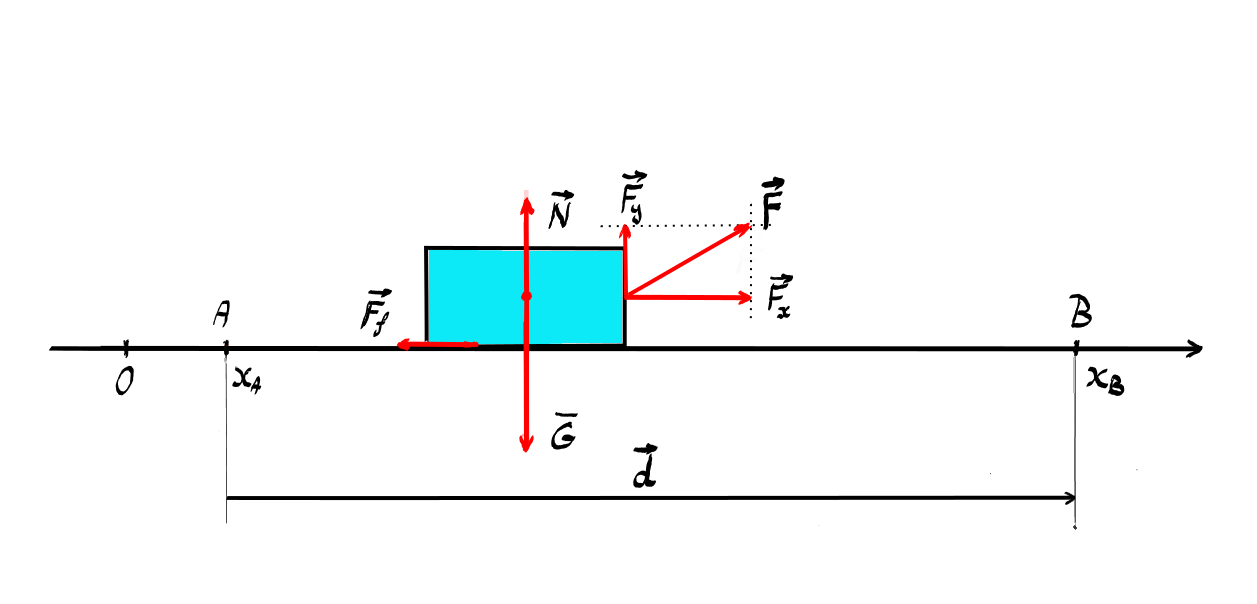
Să considerăm un exemplu simplu
un corp de masă M Care este tractat
de o forță f ce face un unghi Alfa
cu suprafață orizontală astfel
încât el se deplasează cu accelerație
0 Deci are viteză constantă și
obținem o deplasare de datorită
acestei forțe motoare dorim să
calculăm lucrurile mecanice ale
tuturor forțelor ce acționează
asupra corpului forțele sunt bineînțeles
forța motoare s greutatea corpului
gem forța normală Care este reacțiunea
suprafeței la acțiunea corpului
asupra ei prin greutatea corpului
și forța de frecare scriem ecuația
fundamentală a dinamicii și anume
că Forța F plus suma tuturor forțelor
f plus plus G Plus s forța de frecare
este egal cu m a care în cazul
nostru este 0 după cum am rezolvat
de multe ori în capitolul de mecanică
în eutin iarnă în probleme similare
vom proiect această ecuație pe
cele două axe de coordonate o x
și o y și y obținem următoarele
ecuații pe axa o x obținem f cosinus
de Alfa este egal cu forța de frecare
pe axa o y avem că forța normală
plus f sinus de Alfa proiecția
forței f pe o y este egal cu g
Care este m g din prima ecuație
rezultă că cosinus de Alfa este
egal cu n din ce avea două ecuație
rezultă că n este egal cu mg minus
f sinus de a cu plângere Două ecuații
obținem ecuația pentru Forța F
care este un gem împărțit la cosinus
de Alfa minus sinus de a acum suntem
pregătiți să calculăm lucrurile
mecanice în primul rând lucrurile
mecanice ale forțelor n g și ca
componentei vor fi egal cu zero
prin definiție pentru că ele sunt
perpendiculare pe deplasarea produsă
de de l lucrul mecanic al lui n
este egal cu lucrul mecanic al
lui G este egal cu lucrul mecanic
al lui f y și toate sunt egale
cu 0 nu produc deplasare deși corpul
se deplasează rămân în forțele
f x și astea doar componenta orizontală
bineînțeles fx va efectua un lucru
mecanic acesta este lucrul mecanic
motor deci el x va fi mai mare
ca 0 2 când lucrul mecanic al forței
de frecare este un lucrul mecanic
rezistent el se opune deplasării
și va fi mai mic decât 0 putem
calcula direct l s x este egal
cu x x înmulțit cu de Deci este
cosinus de Alfa înmulțit cu de
și în concluzie putem scrie că
lucrul mecanic al forței f care
se datorează doar componente a
lui componente a orizontale este
egal cu minus lucrul mecanic al
forței de frecare și este egal
cu m g de împărțit la 1 minus tangent
de Alfa și în felul acesta Am calculat
lucrurile mecanice ale tuturor
forțelor implicate un ultim comentariu
dacă forța ce efectuează lucrul
mecanic face un unghi Alfa cu deplasarea
precum avem în acest exemplu lucrul
mecanic se calculează folosind
componentă a forței de alungire
deplasări exact cum a făcut noi
deci lucrul mecanic al forței f
este egal cu lucrul mecanic al
componentei de a lungul deplasării
epic Deci în cazul general va fi
f Forța f înmulțită cu deplasarea
înmulțită cu cosinusul unghiului
dintre ele dintre forța motoare
și forța și deplasarea produsă
de ea în general lucrul mecanic
efectuat de o forță f pentru a
deplasa un corp între două puncte
a și b începem două puncte a și
b și Forța F deplasează corpul
de la punctul A la punctul s în
general lucrul mecanic efectuat
depinde de drumul ales dacă alegem
Alt drum sau alta traiectorie obținem
alte valoarea lucrului mecanic
deoarece bineînțeles drumul este
diferit pe traiectorii diferite
există însă forță numită forțe
conservativ a pentru care lucrul
mecanic efectuat nu depinde de
acces de la acest drum sau de această
traiectorie mai precisă el depinde
doar de poziția punctului inițial
și a punctului final și nu traiectoria
luată între cele două puncte exemple
sunt forțele gravitațională sau
greutatea forța și forța elastică
pentru a da un exemplu Să considerăm
un corp de masă M care poate ajunge
din punctul A pe suprafață orizontală
având două fracturi prima este
traiectoria verticală dealungul
segmentului a b c d a doua de a
lungul segmentului ac Spre exemplu
pe un plan înclinat pe care presupunem
că nu există frecare calculăm cele
două lucruri mecanici lucrul mecanic
al greutății gem pe traiectoria
apei este egal cu g ori ab adică
e este egal cu m g greutatea înmulțită
înmulțit cu h înălțimea sau înălțimea
la care se află punctul A față
de punctul b de cel de al doilea
drum lucrul mecanic al greutății
deci pe drumul AC este egal cu
g înmulțit cu sinus de Alfa deoarece
am spus că întotdeauna trebuie
să Considerăm componenta forței
motoare de a lungul deplasării
Deci deplasarea noastră este larmă
planului înclinat acesta este unghiul
Alfa Deci componenta forței motoare
Care este g de a lungul deplasării
va fi aceasta care este sinus de
el deci desolace de Alfa muncit
cu ace Care este lungimea planului
înclinat Dar el este egal cu h
împărțit la sinus de Alfa repet
din nou îl Considerăm că nu există
frecare in acest caz Deci obținem
că acest lucru mecanic este egal
cu mg sinus de Alfa înmulțit cu
h împărțit la sinus de în concluzie
lucrul mecanic al greutății este
același pe ambele traiectorii ab
și ac și este egal cu m g h greutatea
fiind un exemplu de forță conservativă
valoarea lucrului mecanic este
aceeași pe două trei victorii diferite
o proprietate particulară importantă
a forțelor conservative este că
lucru mecanic pe o traiectorie
închisă este 0 Deci dacă plecăm
dintre un punct A și ne deplasăm
pe o traiectorie oarecare dar întorcând
netot în punctul A lucrul mecanic
va fi un exemplu foarte simplu
este cel al unui corp vedem un
corp de masă M și greutate G aruncat
pe verticală de Cielo urcă până
la înălțimea H și apoi coboară
înălțimea h lucrul mecanic total
al greutății este egal cu suma
dintre lucrul mecanic la urcare
și lucrul mecanic la coborâre la
urcare greutatea G este forța rezistent
ia se opune mișcării corpului și
Deci lucrul mecanic va fi minus
mgh la coborâre greutatea are aceeași
direcție ca și deplasarea corpului
De ce este forța motoare ia ajută
la deplasarea sau cauzează deplasarea
corpului și Deci lucru mecanic
va fi pozitiv plus mch În consecință
lucrul mecanic total este 0 interpretarea
geometrică a lucrului mecanic spune
că lucrul mecanic al unei forțe
f Ce produce o anumită deplasare
este egală este egal cu aria de
sub graficul funcției f dealungul
deplasării D pentru a exemplifica
cu cel mai simplu exemplu posibil
această ecuație Să considerăm o
forță Constanța Deci acesta este
graficul forței f care se măsoară
în eutin ca funcție de deplasarea
de care se măsoară în metri în
cazul în care Forța este constant
atunci funcția va fi o dreaptă
orizontală Deci funcția Valoare
valoare constantă să spunem esdrom
În toate punctele de plasării care
are loc între punctele a și b după
cum știm lucrul mecanic al unei
forțe constante este sport d f
în cazul acesta forța Constantin
Ziarul f0 este înălțimea acestui
dreptunghi și de este lungimea
și lățimea o lungimea Deci lucrul
mecanic mod Evident este egal întradevăr
cu aria de sub graficul funcției
f ca funcție de de bineînțeles
această ecuație este dată în general
nu numai pentru forțe constante
ce putem folosi pentru un caz particular
și anume pentru a calcula lucrul
forță elastică forța elastică este
dependentă de deplasare a produsă
deoarece este egală cu minus forța
deformatoare după cum știm din
lecția despre forța elastică și
egală cu minus Constanta elastică
înmulțită cu de vectorul deplasare
x Deci forța elastică este o forță
care nu e constantă ce depinde
de deplasare a produs dacă prezentăm
graficul funcției forței elastice
ca funcție de de formarea sau deplasarea
produse x în cazul acesta deplasarea
este deformarea resortului Ea este
dependentă cu o dependență liniară
de această de formare și putem
calcula lucrul mecanic folosind
această ecuație generală ca fiind
aria graficului de sub funcții
Deci aria a jurat această arie
această formă geometrică este cea
a unui trapez dreptunghic și din
geometrie știind că aria trapezului
dreptunghic este suma dintre baza
mare și bază mică înmulțită cu
înălțimea și împărțită la 2:00
în cazul nostru baza mare este
valoarea forței elastice în punctul
X2 Deci e f e în X2 plus bază mică
care va fi valoarea forței elastice
în punctul X1 sau pentru deformarea
sau deplasare X1 împărțit la 2
cu mulți cu înălțimea înălțimea
h a trapezului este x 2 minus x
1 și apoi înlocuim forța elastică
tu ce obținem minus kx-2 minus
kx1 Împărțiți la 2 înmulțit cu
x 2 minus x 1 de unde rezultă că
lucrul mecanic al forței elastice
este egal cu minus ca împărțit
la 2 mulți cu X2 pătrat minus x
1 pătrat Aceasta este o aplicație
directă a ecuației Ce rezultă din
interpretarea geometrică a lucrului
mecanic

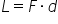
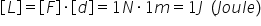
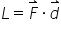
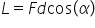
.png)
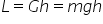
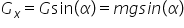
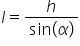
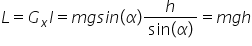
.png)
.png)