Mişcarea circulară uniformă: mărimi caracteristice, acceleraţia centripetă.

începe patra lecții de mecanică

în italiană discutăm despre mișcarea

circulară uniforma mișcarea circulară

uniformă a unui mobil are loc atunci

când traiectoria sa este un cerc

și modulul vitezei momentane este

constant așa cum se arată în această

ecuație vorbim subliniezi doar

de modulul și nu de Direcția vitezei

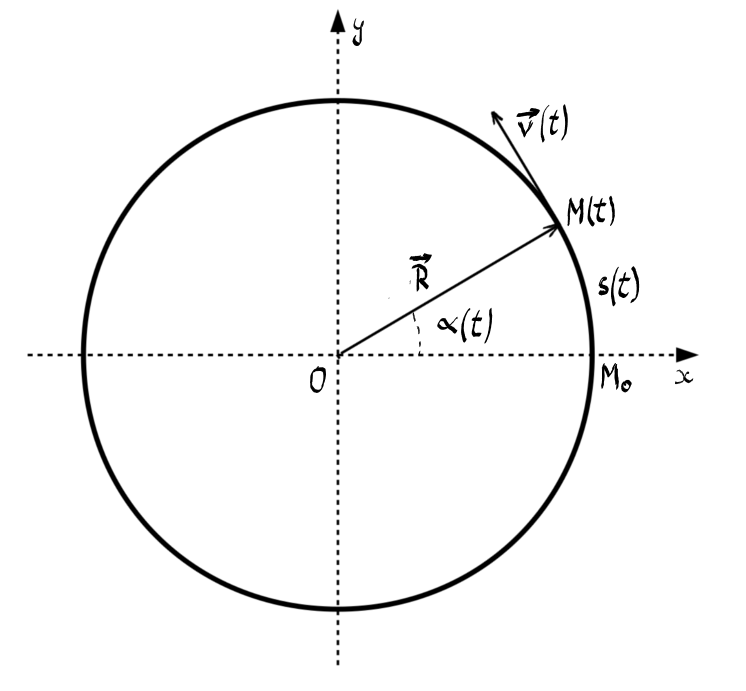
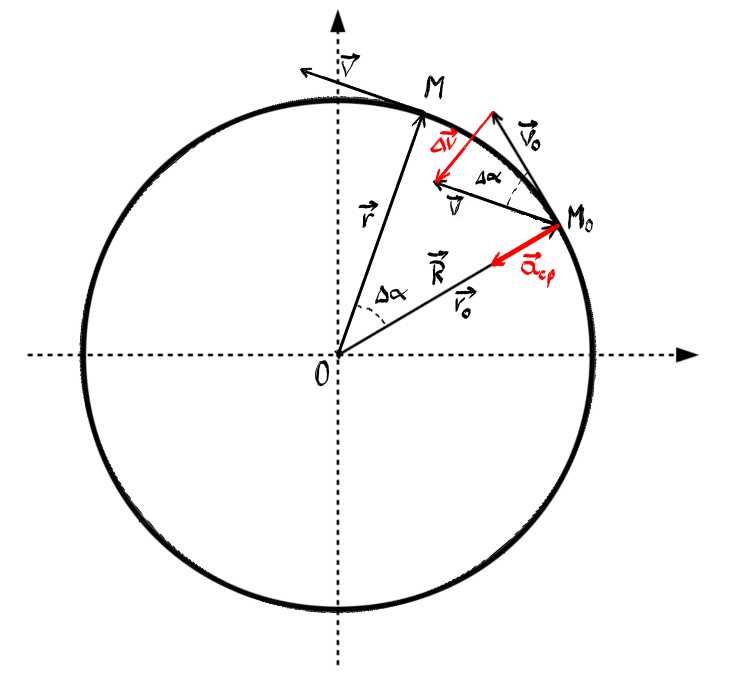
această schemă prezintă elementele

de bază ale unei mișcări circulare

mobilul se află în poziția m0 la

momentul t0 și apoi în poziția

m La un anumit moment te poziția

vectorul poziție este notat cu

r și vectorul viteză cuv reamintesc

că în lecția a doua am demonstrat

că pentru o mișcare circulară viteza

momentană este perpendiculară pe

vectorul poziție așa cum vedem

aici Vita viteza vesti tangențială

la traiectorie între o mișcare

circulară uniformă mobilul descrie

arce de cerc egale în intervale

de timp egale Asta bineînțeles

datorită vitezei sale constant

de asemeni putem observa că vectorul

poziție are un modul constant și

anume egal cu raza traiectoriei

în consecință ecuația de mișcare

va fi dată de orientarea modul

de orientarea vectorului poziție

Acest lucru se poate face în două

feluri și anume precizarea legii

descrise de orientarea vectorului

poziție rdt În primul rând putem

specifica ecuația pentru unghiul

acestui Vector de poziție notat

în schema noastră cu alfa de ten

Alfa se numește și a ști sau unghiulară

al doilea fel de a specifica orientarea

vectorului poziției este aceea

de a da ecuația abscisei curbilinii

s d t s deteste lungimea arcului

traiectoriei deschis de mobilul

m de ce avem două forme alternative

de specificare a ecuației de mișcare

mai exact a orientării vectorului

poziții putem da ecuația pentru

a ști sau unghiulară sau pentru

abscisa curbilinii ele sunt legate

prin relații simplă abscisa curbilinie

s de taste egală cu raza traiectoriei

care o constantă înmulțită cu abscisa

unghiulară Alfa de te este important

de ținut minte că aceasta este

ecuația este valabilă dacă unghiul

Alfa este măsurat în radiani și

nu în grade am radianul este o

unitate de măsură alternativa unghiurilor

față de grad Pentru a stabili relația

dintre cele două unități de măsură

a unghiurilor observăm că o rotație

completă corespunde unui unghi

de 360 de grade iar în radiani

aceasta corespunde unei circumferințe

complete Deci 2 înmulțit cu aer

aceasta este circumferință a unui

cerc cu rază r împărțită la aer

Deci din nou Alfa care corespunde

unui unei rotații complete de 360

de grade este egal cu s pentru

o rotație completă Deci 2 pi R

circumferința cercului împărțit

la R Da deci în radiani acest unghi

va fi doi i în radiani de aici

obținem ecuația care leagă gradele

de radiani Deci dacă avem un unghi

Alfa măsurat în radiani trebuie

să împărțim la doi pini pentru

a obține valoarea pentru același

unghi dar exprimat în grade împărțit

la 360 parametrii mișcării circulare

uniforme sunt legate de faptul

că mișcarea este periodică adică

după o rotație completă mișcarea

este repetă identic Deci numim

perioadă te durata unei astfel

de rotații complete după care mișcarea

se repetă identic numim frecvență

a rotației notată cu un you numărul

de rotații complete în unitatea

de timp deci frecvența este inversul

perioadei și în consecință ia are

ca unitate de măsură secunda la

minus 1 Care este notată în sistemul

internațional de referință pentru

unități de măsură cu hărți Deci

o secundă la minus unu se mai numește

și un hertz următorul parametru

este viteza liniară se numește

viteza liniară notată cu viteza

medie a f și se curbilinii din

definiția vitezei medii putem scriu

imediat că viteza liniară este

Delta spre Delta t viteza medie

aduc aminte Era Delta XP Dell tot

a scris în funcție de exciza curbilinie

va fi Delta is împărțit la deal

tate ia poate fi foarte ușor calculată

dacă calculăm acest raport pentru

o rotație completă pentru că atunci

Delta Est suc urbi linie pentru

o rotație completă este circumferința

cercului cel prezentat traiectoria

de ce este 2 pi r iar Delta TVA

fiti Care este durata unei rotații

complete Deci viteza liniară va

fi 2 Pierre împărțit la test sau

doi Petre înmulțit cu frecvența

în you o adori a doua viteză care

se calculează este viteza unghiulară

notată cu Omega acesta este viteza

medie a celelalte și se ceai unghiulară

Deci seminar definiției va fi Omega

Regal sau definit cu Delta l fam

mulți cu Delta t la fel ia poate

fi ușor calculată Considerând o

rotație completă Omega pentru rotație

completă va fi unghiul complet

exprimat în radiani pentru rotație

completă Care este 2 împărțit la

timpul unei rotații complete Care

este perioada de Omega este 2 prin

părțile astea sau 2 pi ori frecvența

nu relația dintre cele două viteze

liniară și cea unghiulară este

imediată din aceste Două ecuații

și anume vei este egal cu un mega

ori vom continua cu calculul accelerației

între o mișcare circulară uniformă

care se numește accelerația centripetă

ia apare datorită modificării direcției

vectorului viteză în fiecare moment

deși magnitudinea sau modulul vectorului

viteza este constant avem un exemplu

foarte interesant de consecință

a modificării direcției numai a

unui Vector că atunci când magnitudinea

lui rămâne constantă în particular

viteza are modul Constanța direcție

variabilă în această tip de mișcare

Considerăm aceeași schemă în care

Un mobil aflat la momentul t0 în

poziția m0d scrie o mișcare circulară

avem vectorul poziție și vectorul

viteză liniară bem Care este perpendicular

pe vectorul poziție reamintesc

faptul că viteza momentană este

perpendiculară pe vectorul poziție

a fost demonstrat în cele doua

lecție de mecanică newtonian mobilul

se mișcă pe această traiectorie

și la momentul t se află între

nouă poziție desenată cu culoarea

roșie în schema noastră e la parcurs

un unghi de alte Alfa are un nou

Vector de poziție care totuși are

același modul numai orientare diferită

și o viteză care are aceeași modul

dar altă orientare să calculăm

unghiul dintre cei doi vectori

viteză Deci avem primul Vector

viteză și cel de al doilea și ne

interesează să calculăm acest unghi

datorită faptului că vectorii poziție

sunt perpendicular pe vectorii

viteză în ambele situații în ambele

momente între 0 și te obținem că

acest unghi dintre cei doi vectori

viteză este Delta Alfa din nou

pentru că axele sau dreptele ce

Delimitează unghiul vitezelor sunt

perpendiculare pe dreptele ce Delimitează

unghiul pozițiilor și deci putem

desena cele două viteze ca având

aceeași porni în același punct

dorim să calculăm Delta vede și

folosind metoda coadă la coadă

la cei doi vectori cei doi vectori

v au aceeași magnitudine dar orienta

diferită separați de acestui care

am demonstrat că e delta Alpha

iar în cazul când Delta te tinde

la 0 vorbim din nou despre aceleași

variații infinitezimale atunci

și Delta Alpha tinde la 0 acestui

tinde la 0 și Deci cei doi vectori

viteză se vor apropia foarte mult

în limita de el tot a tinde la

0 Și atunci vom obține un Vector

viteză perpendicular pe Delta V

Deci în acest caz limită al variațiilor

infinitezimale Delta V devine perpendicular

pe despre variații infinitezimale

am discutat la sfârșitul lecției

precedente în concluzie deoarece

accelerația este proporțională

cu Delta V rezultă că accelerația

centripetă va fie perpendiculară

pe viteză Deci sensul direcția

și sensul accelerației centripete

sunt următoarele direcții este

aceiași cu vectorul poziție dar

sensul este opus Deci acțiunea

accelerația centripetă va fi dealungul

razei și va indica întotdeauna

ca sens centrul traiectoriei pentru

a calcula magnitudinea sau mă duc

la aceste accelerații vedem că

în această limită a variațiilor

infinitezimale ale unghiului în

cazul acesta putem scrie că Delta

avem este aproximativ egală cu

v înmulțit cu Delta l și atunci

calculăm direct accelerația centripetă

împărțind această relație cu Delta

t și obținem așezați la centripete

egală cu b mulți cu Delta Alfa

împărțit la Delta t iarăși interesant

observăm o accelerație generată

nu prin variația vitezei în modul

și variația orientării vitezei

prin variația direcției vitezei

exprimată prin unghiul Alfa imediat

obținem că accelerația centripetă

este V ori Omega viteza liniară

ori viteza unghiulară pentru că

Delta Alpha împărțirea Delta t

e prin definiție viteza unghiulară

Ia mai poate fi scrisă și ca Omega

la pătrat aur R sau Vela pătrat

împărțit la aer să dăm un exemplu

de situație practică în care folosim

o traiectorie circulară uniforma

să calculăm viteza liniară și accelerația

centripetă pe care o aveți dumneavoastră

chiar în acest moment datorită

rotației Pământului în jurul axei

proprii viteza liniară este exprimată

prin relație ca prezentator de

curând iar accelerația centripetă

iarăși poate calcula în funcție

de viteza liniară prin această

relație această schemă descrie

situația cercul este Pământul care

se rotește în jurul axei proprii

Deci are o rotație ni Dumneavoastră

sunteți punctul d r p este raza

pământului o este centrul pământului

iar dumneavoastră Descrieți rotația

desenată cu roșu în cercul roșu

de raza aer Deci pentru a calcula

raza mișcării dumneavoastră circulare

din acest moment aplicăm relația

R este egal cu arcuri sinus de

90 minus latitudinea latitudinea

este unghiul pe care dumneavoastră

la veți în raport cu Axa cu Ecuatorul

pământului nicio Ce este latitudinea

dumneavoastră aminte respectiv

Deci acestui unghi este 90 minus

de grade minus el și sinus de 90

de grade minus El este R împărțit

la r p datorită faptului că acest

unghi este 90 de grade blonde o

rază aproximativă a Pământului

de 640 de km și considerând că

sunteți la ora actuală în București

să spunem Atunci înseamnă că aveți

o latitudine de 44 de grade și

25 de minute pe care o Vom aproximat

cu 45 de grade caz în care putem

să calculăm raza dumneavoastră

de rotație punând valorile pentru

iar pe și el în relația aceasta

Deci la dacă va aflați în București

aveți o rază aproximativă de 4.500

25 de km luni pentru t perioada

de rotație a pământului 24 de ore

adică o zi atât ia aproximativ

pământului să facă o rotație completă

în jurul axei proprii putem calcula

și de parametri viteza liniară

va fi egală după înlocuirea acestora

date cu 329 de metri pe secundă

este foarte interesant este o viteză

foarte mare pentru comparație amintesc

viteza sunetului Care este egală

cu 343 de m pe secundă Deci la

ora actuală elementul actual stând

pe scaun vă rotiți în jurul pământului

cu o viteză liniară aproape de

viteza sunetului Bineînțeles nu

veți simți nimic deoarece tot ce

se află în jurul dumneavoastră

inclusiv aerul se rotește cu aceeași

viteză Deci Important este că stați

pe loc în raport cu toate obiectele

din jurul dumneavoastră inclusiv

aerul Pământul se învârte cu totul

cu toate aceste obiecte incluzând

vă pe dumneavoastră cu această

viteză la punctul la care va frați

accelerația centripetă iarăși foarte

interesant îi iese din calcul foarte

mică este de ordinul al 2c m pe

secundă la pătrat reamintesc că

accelerația gravitațională care

descrie greutatea dumneavoastră

datorită atracției Pământului accelerației

gravitaționale este aproape 10

m pe secundă la pătrat Deci deși

viteza liniară cu care vă rotiți

dumneavoastră și tot ce este înjură

dumneavoastră este foarte mare

aproape de viteza sunetului accelerația

Ce rezultă din această rotație

este foarte mică neglijabilă în

raport cu alte accelerații la care

sunteți sub
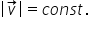
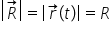
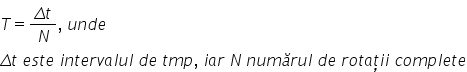
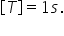
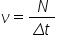
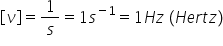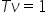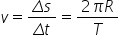
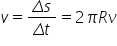
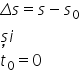
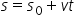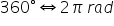
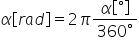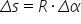
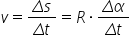
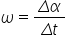
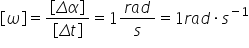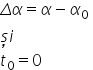
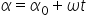
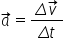
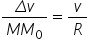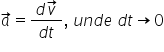
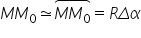
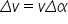
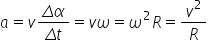
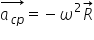