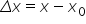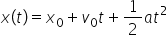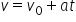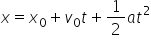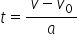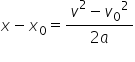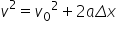Mişcarea rectilinie uniform variată: ecuaţia de mişcare şi relaţia Galilei.
Tag-uri
Partajeaza in Google Classroom

Transcript
În ce an a treia lecții de mecanică
newtoniană vom discuta despre mișcarea
rectilinie uniform variată să începem
cu definiția aceste mișcări mișcarea
rectilinie uniform variată mobilul
are loc atunci când traiectoria
este rectilinie și vectorul accelerație
este constant de aici vine numele
de mișcare uniform variată și anume
viteza unei asa de mișcări se schimbă
în timp dar la o rată de schimbare
constantă de cea crește sau scade
uniformă în timp deci uniform variată
di definiția accelerației medii
pe care am dat în lecția trecută
nu putem scrie că accelerația medie
este egală cu viteza finală minute
viteza inițială împărțită la momentul
final minus momentul inițial al
mișcării și în concluzie această
cantitate este o constantă în cazul
mișcării despre care vorbim amintesc
că în general această accelerație
medie este o funcție de Delta t
în cazul mișcării rectilinii uniform
variate această dependență nu mai
are loc dacă alegem sistemul de
referință astfel încât t0 să fie
egal cu 0 Deci nu mai avem un moment
inițial în acei coacem obținem
direct din această relație legea
vitezei și anume V ca funcție de
timp este egal cu zero plus a înmulțit
cute important De notat în această
ecuație este că singura variabilă
în partea dreaptă a relației este
timpul te vezi roșii ei fiind două
constante iar important De notat
este că avem două tipuri de mișcări
care corespund unui semn pozitiv
al accelerației sau nu e semn negativ
al accelerației mișcarea în care
accelerație este pozitivă se numește
accelerată iar cea în care același
este negativă se numește decelerate
sau frânată Următorul pas este
deducerea legii de mișcare a ecuației
de mișcare adică a dependenței
poziții x de timp pentru aceasta
pornind de la definiția vitezei
medii care a fost dată și Ana lecția
trecută și anume viteza medie Care
este o funcție de Delta t este
Delta x împărțit la Delta t reamintesc
Delta x este x minus X 0 și Delta
t este Termină stă 0 dar în cazul
nostru am considerat că te zero
este egal cu 0 Deci Delta t este
în concluzie obținem că x este
egal cu x 0 plus produsul dintre
viteza medie Care este o funcție
de Delta teșite această ecuație
nu poate fi considerată încă o
ecuație de mișcare pentru că între
ecuație de mișcare am avea în partea
dreaptă a ecuației toți termenii
mai puțin timpul ca și constante
Deci pentru a obține cu adevărat
ecuație de mișcare adică explicită
trebuie să calculăm viteza medie
ca funcție de timp și să înlocuim
această ecuație pentru a face acest
lucru de motoare ma imediat pe
care nu o voi demonstra și numai
o voi formula și apoi o voi folosi
pentru a calcula această viteză
Metan totuși la sfârșitul acestei
lecții voi face câteva comentarii
Apropo de această teoremă Deci
renunțarea unei teoreme valoarea
medie a unei funcții f de x în
intervalul X1 X2 este dată de această
formulă macar eu valoare un număr
valoarea medie a funcției f de
x din intervalul Sonic 2 egal cu
a unde a este aria delimitată de
funcții și axa o x între valorile
X1 și X2 unde calculăm media și
diferența dintre X2 și deoarece
imediat voi folosi această teoremă
pentru a calcula viteza medie nu
mai dau niciun alt exemplu pentru
această teoremă matematică vom
vedea cum funcționează Cum se aplică
direct pentru cazul nostru și anume
unde funcția f de x este de fapt
vedete Deci pentru a obține cu
ața de mișcare folosim această
teorema știm că și am demonstrat
că legea vitezei este vede t egal
cu zero plus ape unde din nu vă
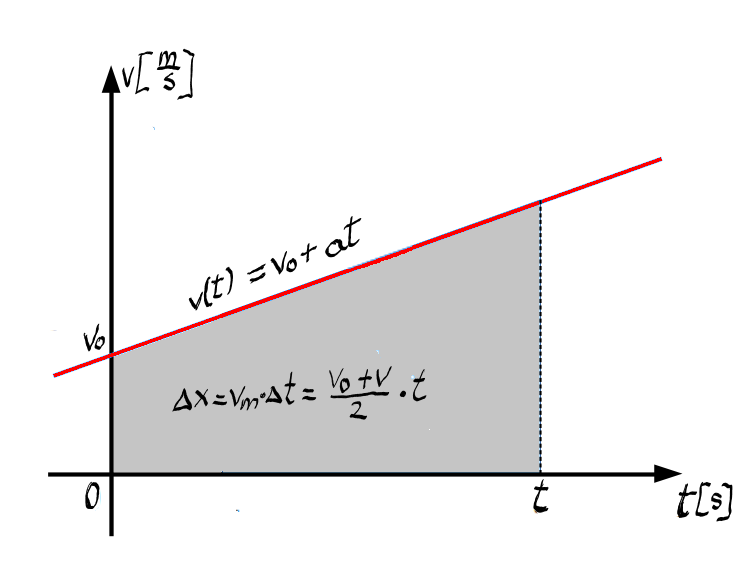
062 constante acest grafic arată
această dependență și a legii vitezei
și anume văd pe axa verticala din
viteza măsurat în metri pe secundă
pe axa orizontală a venit timpul
măsurat în secunde iar această
dreaptă este funcția noastră și
anume vdt este egal cu 0 plus f
Da avem o dependență liniară de
timp care la momentul 0 egal cu
0 vedem că b este egal cu 0 Deci
la timpul 0 funcția trece prin
punctul zero și apoi avem o pantă
care dată de accelerația constantă
a și apoi aplicăm direct teorema
pe care am discutat doar pe care
am prezentat în acest caz Deci
funcția noastră f de x din acea
teoremă este vedete Deci vom avea
f funcția corespunde funcției noastră
viteză iar coordonata x corespunde
coordonatei noastre te argumentului
tetina intervalul pe care facem
calculul vitezei medii este corespunde
lui X1 Care este 0 egal cu 0 și
X2 va corespunde momentului final
te da Deci facem înlocuirile tuturor
acestor relații de substituție
în relația noastră pentru valoarea
medie a funcției Deci valoarea
medie a vitezei este egală cu aria
de sub grafic pe care o va arăta
imediat împărțită la x 2 minus
x unul care în cazul nostru va
fi minus 0 Deci împărțit la Tei
are de sub grafic este aria de
sub graficul funcției noastre Care
este vedete în intervalul în care
vrem să calculăm media și anume
0 De ce este aria pe care o coșurile
ziua acum aria de sub grafic în
intervalul considerat 0 în cazul
nu deci viteza medie este aria
hașurată împărțită la timpul te
observăm că aria hașurată este
un trapez dreptunghic a stat deoarece
avem unghiul de 90 de grade în
aceste două puncte și aria unui
trapez dreptunghic din geometrie
știind că este egală cu suma dintre
baza mare a trapezului și bază
mică înmulțită cu înălțimea trapezului
împărțit la 2 în cazul graficului
nostru baza mare este viteza finală
bază mică este v0 viteza inițială
și înălțimea este timpul trecut
Deci aria este V Plus b0a cu timpul
împărțit la 2 deci viteza medie
se va obține împărțind această
relație lapte în concluzie viteza
medie va fi vplus.ro împărțit la
2 ne aducem aminte că Ultima relație
pentru ecuația de mișcare pe care
o avea era x egal cu 0 plus vm
înmulțit cu timpul și toată tot
acest exercițiu care îl am făcut
până acum este pentru a scrie o
ecuație explicită pentru viteza
medie ceea ce am făcut Deci facem
substituția și obținem că x este
egal cu x 0 plus 0 plus z împărțit
la 2 înmulțit cu timpul și în fine
știm că v ă cest V de aici depinde
de timp intră lege dată de lege
vitezei și anume 0 plus ATE făcând
aceasta soție finală aici obținem
că x este egal cu x 0 plus v0 pentru
că avem doi de zero și Deci împărțit
la 2 văd aveți zero înmulțit cu
timpul și în final plus jumătate
din a morții cu timpul la pătrat
aceasta este ecuația de mișcare
pentru mișcarea rectilinie uniform
variată vând continuă cu deducere
relației Galilei Până acum am găsit
veri legi pentru mișcarea rectilinie
uniform variată în care singura
variabilă explicită era timpul
celelalte fiind constante în relația
Galilei eliminăm timpul din legea
vitezei și ecuația de mișcare pentru
a obține o dependența vitezei de
distanță a parcurs reamintesc viteza
legea vitezei Era vdt ca funcție
de taste egal cu 0 plus a t unde
din nou singura variabilă este
timpul t v 0 6 în constante iar
viteza medie Era definită ca Delta
x împărțit la Delta t unde rezultate
în cazul nostru era egal cu timpul
pe pentru că am ales un sistem
de referință în care te zero Raica
Cuza și procedăm la eliminarea
timpului din aceste ecuații în
pentru prima parte a ecuației Delta
x egal cu viteza medie ori timpul
vedem că o putem obține direct
din definiția vitezei medii Delta
x egal cu viteza medie înmulțit
cu timpul viteza medie tocmai am
de dus so pentru acest tip de mișcare
și este V Plus v 0 împărțit la
doi Deci Delta x este egal cu a
plus b 0 împărțit la 2 înmulțit
cu timp și în sfârșit din legea
vitezei V egal cu zero plus a ori
te eliminăm timpul Deci timpul
este minus 0 împărțit la Care este
ultima ultimul termen din această
ecuație în concluzie putem scrie
că 2-a înmulțit cu Delta x este
egal cu acest produs de la Numărător
care este V pătrat minus v0 pătrat
și în final putem obține așa numita
relație Galilei care spune că viteza
la pătrat este egală cu viteza
inițială la pătrat plus 2-a ori
Delta Delta X1 mișcarea efectuată
între cele două momente de 07 un
tip particular de mișcare uniformă
var uniform variată este mișcarea
uniform încetinită este mișcarea
rectilinie frânată cu accelerație
Constanța A deci explicând explicit
faptul că accelerația este negativă
Asta înseamnă de celalalt sau frânată
scriem că a este egal cu minus
modulul lui a acest minus arată
explicit faptul că accelerația
este negativă să calculăm timpul
de oprire în mișcare uniform frânat
pentru aceasta punem condiția ca
viteza finală să fie egal cu 0
Asta înseamnă oprire neam oprit
viteza este final este 0 punând
v egal cu 0 în legea vitezei aceasta
de sus Deci vei final este 0 obținem
că vezi zero plus a care devine
minus Modul din a înmulțit cu timpul
în acest caz timpul de oprire este
egal cu 0 Deci obținem că timpul
de oprire între o mișcare uniform
frânată sau încetinită este viteza
inițială împărțită la modulul accelerație
pentru a calcula distanța de oprire
punem aceeași condiție și anume
v egal cu 0 viteza finală egal
cu zero în relația Galilei și obținem
că viteza inițială la pătrat minus
doi a modul din ar fi trebuit să
scriu aici Deci 2 modul din am
înmulțit cu distanța de oprire
este egal cu 0 Deci distanța de
oprire este viteza inițială la
pătrat împărțit la 2 ori modulul
lui a și în sfârșit va promis o
discuție în legătură cu teorema
din această lecție În încercarea
de a dezvolta teoria mecanicii
clasice Newton A remarcat că există
câteva tipuri de probleme ce nu
pot fi modelate cu ajutorul matematicii
existente pe vremea lui aceeași
timp de problemă aveți și dumneavoastră
acum pentru că în clasa a 9-a Când
se face mecanica clasică există
anumite noțiuni de matematică ce
vor fi făcute în clasa a 12-a Care
sunt foarte utile în dezvoltarea
modelelor cinematici Despre ce
vorbim în primul tip de mărimi
despre care pentru care avem nevoie
de o matematică mai evoluată sunt
așa numitele mărimi momentan raportate
la variații infinitezimală x mai
exact ați întâlnit astfel de mărimi
Delta Delta x tinzând către 0 sau
infinitezimal so foarte mic în
lecția trecută în special în Definirea
vitezei medii viteza medie accelerația
medie dar poate și mai mult viteza
momentană și accelerația momentană
erau definite folosind acest concept
de variație infinitezimal când
această variație este suficient
de mică când Delta t este suficient
de mic nu am discutat acest subiect
și nu mai am prezentat conceptul
în general Și am trecut mai departe
aceasta Problema este rezolvată
în analiza matematică sau calculul
diferențial notând această cantitate
cu așa numita derivată de e y la
de x și în felul acesta dezvoltând
întregul aparat matematic care
adresează problemele legate de
variații infinitezimale un alt
sat în al doilea set de mărimi
pe care Newton la întâlnit și pentru
care nu avea o soluție matematică
sunt marile mărimile medii ale
unei mărimi y3 rează continuu întrun
interval X1 X2 Deci cum am avut
yx-1000a Tică vdt viteza erau mărime
si variat continuu în funcție de
timpul te întâlnit urval 0 și pentru
aceste mărimi trebuie calculate
mărimi medii în pentru interval
dat pentru a Ce este mărimi în
analiza matematică introduce integrala
conceptul de integrală Deci această
mărime medie este integrala de
la X1 la X2 din y3 x x nu trebuie
bineînțeles să știți în clasa a
noua nici derivata nici integrală
ele vor fi făcute în clasa A 12-a
dar trebuie să știi util să știți
De unde vin anumite concepte de
matematică legate de cinematică
si el ca un comentariu revenind
la Newton În încercarea sa reușită
de a găsi legile mecanicii clasice
a cinematicii în acest caz a fost
nevoit să dezvolte o nouă ramură
a matematicii împreună cu alți
avanti vremii sale Deci Newton
încercând să dar dezvolte legile
cinematicii până la capăt a fost
nevoit să dezvolte primele versiuni
ale calcului infinitezimal derivate
și a calcului integral integralele
pentru a calcula până la capăt
mărimile cinematicii analiza matematică
de ceea ce este conținut de matematică
se studiază în clasa a


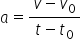
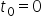 ,
,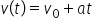 .
.
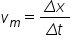 .
.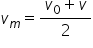
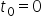
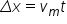
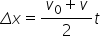
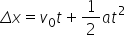 ,
,