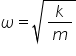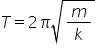Mişcarea oscilatorie. Mişcarea oscilatorie armonică. Pendulul elastic.
Tag-uri
Partajeaza in Google Classroom

Transcript
în prima lecție despre oscilații
și unde mecanice vom discuta despre
mișcarea oscilatorie în general
Și apoi despre mișcarea oscilatorie
armonica oscilația este mișcarea
ce se repetă periodic sistemul
revenind în poziția inițială după
fiecare perioadă exemple de oscilații
de sisteme care descriu mișcării
oscilatorii sunt pendulul vibrația
unei corzi electronii în curent
pentru un curent alternativ atomii
în rețeaua unui cristal și așa
mai departe pentru a vizualiza
o mișcare oscilatorie am introdusă
această imagine cu un copil care
se dă în leagăn observăm că aceasta
este oscilație pentru că se repetă
periodic după un anumit timp copilul
revin în aceeași poziție inițială
iar timpul după care revin în această
poziție inițială se numește perioada
oscilații mărimile caracteristice
oscilații sunt următoarele În primul
rând după cum am spus este perioada
perioada care se notează cu t și
bineînțeles fiind un interval temporar
se măsoară în secunde este timpul
după care o știi la torul revin
în același punct mișc în dusei
în același sens important această
observație mișcând în același sens
pentru că în timpul unei perioade
corpul sau și la torul trece printr
un punct de două ori Spre exemplu
Acest copil va trece prin poziția
de la baza leagănului de două ori
O dată când se duce și apoi când
se întoarce vorbim despre trecerea
unei perioade semnificând intervalul
de timp în care el trece prin același
punct dar mișcând se în același
sens Deci dacă considerăm punctul
de la baza leagănului o perioadă
va fi ferrada în care băiatul se
duce trece prin punctul de la baza
ajunge la maxim se întoarce ajunge
din nou la punctul de la baza dar
asta nu este încă o perioadă pentru
că se mișcă în sens invers față
de momentul când a trecut prima
dată urcă și apoi coboară încă
o dată atunci avem o perioadă Deci
revenirea în același punct mișcarea
sa în același sens definește o
perioadă elongația y este distanța
oscilatorului față de poziția de
echilibru în cazul băiețelului
poziția de echilibru este punctul
de la bază în acea poziție el rămâne
pe loc fără a mai oscila Deci aceasta
este poziția de echilibru a oscilației
leagănului iar elongații va fi
distanța dintre această poziție
de echilibru de la bază și poziția
de la un moment dat te amplitudinea
oscilației este locația maximă
adică în cazul acestui desen aceste
imagini distanța dintre punctul
de la baza leagănului și punctul
maxim de ridicare a lacului a copilului
în leagăn aceasta se numește amplitudinea
oscilației frecvența oscilației
sunt Notează cu u și este numărul
de oscilații în unitatea de timp
Deci definiția în general a lui
nu este numărul de oscilații pe
timpul trecut dar prin definiția
perioadei timpul este numărul de
oscilații înmulțit cu timpul unei
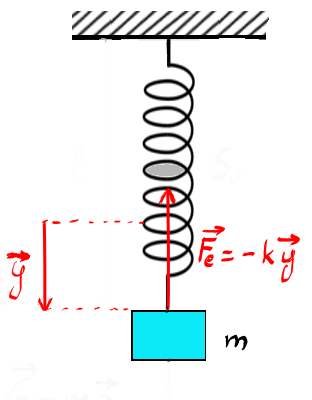
oscilații și în concluzie frecvența
este inversul perioadei se măsoară
în hărți Deci unitatea de măsură
pentru frecvență este un hărți
de asemeni bineînțeles definim
o viteză momentan 25 la ție Care
este variația viteza de variație
al Ungariei y și o accelerație
momentană 25-a care e viteza de
variație a vitezei 25 să discutăm
acum despre mișcarea oscilatorie
armonică dar o Vom defini nu Imediat
Și după ce o Vom introduce să spunem
întâi că majoritatea mișcărilor
oscilatorii ne disipative adică
în care nu există sau neglijăm
forțele de frecare poți modelate
matematică prin proiecția pe o
axă a mișcării circulare uniforme
de școală în proceda vom considera
o mișcare circulară uniformă pe
care o Vom proiecta pe o axă și
vom obține astfel o mișcare oscilatorie
spunem că majoritatea mișcă norii
sunt deschise în felul acesta dar
după aceea vom demonstra că prin
acest cuvânt majoritatea înțelegem
de fapt mișcările oscilatorii armonice
majoritatea a mișcărilor oscilatorii
ne disipative sunt armonice și
în felul acesta vom introduce în
mișcare oscilatorie armonică să
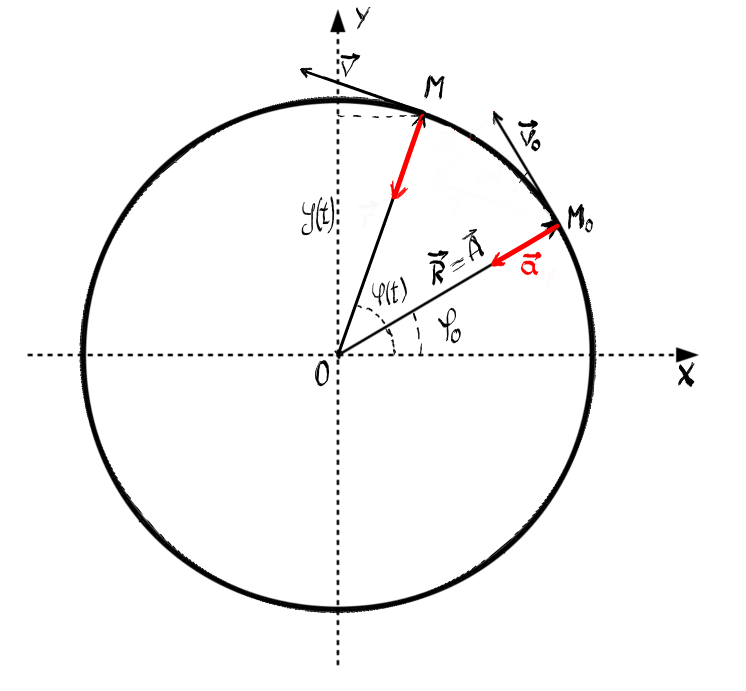
procedăm pornind de la o mișcare
circulară uniformă pe care o vedeți
în această schiță de ce vedeți
este un mobil notat cu m care descrie
o mișcare circulară uniformă pe
acest cerc în planul deschis de
axele de coordonate o x și o y
Deci mișcare circular uniformă
înseamnă că modulul vitezei mobilului
este constant vectorul v m vitezei
modulului este o constantă dacă
notăm cu m 0 poziția inițială a
modului mișcarea sa aflată la unghiul
fi 0 față de axa x și cu m poziția
mobilului la momentul t atunci
poziția lui va fi descrisă de unghiuri
fie la momentul te acest unt la
momentul t m este egal cu viteza
unghiulară Omega înmulțită cu timpul
plus fizzer viteza unghiulară Omega
se mai numește și pulsații această
ecuație apare direct din definiția
vitezei unghiulare viteza unghiulară
este prin definiție variația unghiului
în unitatea de timp dar Delta fii
este fii minus fi 0 iar Delta t
este tempeh Considerăm tezeul egal
cu 0 și de aici obținem că fii
este omega-3 plus size De ce si
Asta este ecuația pentru unghiul
fiice de scriem poziția la momentul
t oarecare a mobilului în mișcarea
sa circular uniform paramedicii
descriu această mișcare sunt poziția
Deci vectorul R viteza v m și accelerația
centripetă vă rog să recapitulat
lecția de cinematică în care am
de scris mișcarea circulară uniformă
unde veți vedea ecuațiile pentru
viteza și accelerația centripetă
în acest tip de mișcare acum să
facem pasul următor și anume să
proiectăm această mișcare circulară
uniforma adică parametri iei pe
o axă putem să alegem atâta axa
o y cât și axa o x obținem aceeași
lucru o proiectăm pe o y proiectare
ca funcție de ten și obține y10a
vom proiecta viteza avem și Vunk
ține V și vom proiecta de asemeni
accelerația centripetă A m și vom
obține a vectorul a y vectori ce
descriu mișcarea pe axa o y care
va fi o mișcare oscilatorie deci
în primul rând să proiectăm de
ceai de ten este prin construcție
proiecția lui aer pe axa o y De
ce este ursinus d fie de tei fii
de ter această ecuație deci deteste
ursinus de omega-3 plus Pfizer
observăm că amplitudinea aceste
mișcări pe axa y este egală cu
raza Iar asta deci prin definiție
amplitudinea este rația maximă
și vedem că e lângă cheia maximă
a mișcării pe axa o y este raza
Deci la În valoare maximă y de
te devine Deci amplitudinea mișcării
pe gratis este pe care înlocuie
menu ecuația de sus și obținem
că y este are următoarea formă
a amplitudinea sinus de omega-3
Plus fizzer să proiectăm viteza
Deci viteza V desenată cu roșu
aici va fi vm cosinus de fite pentru
că vedem că acest ucide te este
egal cu acest unghi iar deoarece
v m este perpendiculară pe raza
și v este perpendiculară pe cea
stârnit punctată obținem ca acestia
unghi este de asemeni și de Și
de ce obținem că cosinus de fii
este cateta alăturată împărțită
la ipotenuză Deci va fi vm cosinus
de filete în concluzie de asemeni
vm pentru mișcarea circulară uniforma
viteza știind că este Omega aer
în cazul nostru va fi de asemenea
egal cu Omega și de cine locuind
valorile vitezei între o mișcare
circular uniformă și a unghiului
fie de te în această ecuație obținem
ecuația pentru viteza pe axa y
y y Deci Vede te va fi Omega a
cosinus de Omega teve plus și 0
și în fine proiectăm De asemeni
și accelerația centripetă pentru
a obține a accelerația pe axa OY
deci a d t este egal cu minus a
m sinus de fi DT să luăm în triunghiul
dec sinus definite pentru că acest
unghi este egal cu acest Deci avem
o axă o dreapta comună pentru cele
două unghiuri iar celălalt de două
drepte sunt paralele fiind amândouă
perpendiculare pe o Deci acest
unghi este fie de ten și deci a
este aer sinus de filete este luat
cu semnul minus pentru că această
accelerație se opune sensului de
te deci y300 pe axa o y iar accelerația
are sensul opus axei OY De ce avem
un semn mic datorită orientării
lui A față de axa OY pe care facem
proiecția Da semne din ecuațiile
mișcării circulare uniforme știind
că accelerația centripetă este
Omega pătrat aer sau în cazul nostru
Omega pătrat a amplitudinea fiind
egal facem înlocuirea și obținem
ecuația pentru accelerația pe axa
o y care va fi minus Omega pătrat
a sinus de omega-3 și 0 De ce înseamnă
acesta am putut modela o mișcare
oscilatorie ce ape axa o y pentru
că vedem că Pe măsură ce mobilul
nostru Descrie o mișcare circulară
uniformă proiecția lui pe axa o
y va Descrie o mișcare oscilatorie
periodică în jurul centrului o
ala mișcării Haideți să vedem totuși
De ce această mișcare oscilatorie
se numește armă să luăm în considerare
ecuațiile pe care le am de dus
pentru această mișcare oscilatorie
pentru elongația y de te și accelerația
A deci am de dus aceste Două ecuații
au împreună observăm că putem scriu
următoarea ecuație a am accelerație
este minus Omega pătrat pulsația
la pătrat înmulțit cu Ungaria dacă
înmulțim această ecuație cu masa
oscilatorului obținem forța măsor
accelerație este forța de Ce rezultă
că forța ce acționează asupra oscilatorului
în oscilația de scrisă prin aceste
ecuații va fi egală cu o constantă
care această care Constanța este
egală cu masa ori pulsația la pătrat
o constantă pentru nu depinde de
timp deci o constantă înmulțită
cu elongația observăm că acest
tip de forță este o forță de tip
elastic în care Forța este proporțională
cu elongația dar are semn contrar
prin definiție numi mișcare oscilatorie
armonică mișcarea oscilatorie sub
acțiunea unei forțe de tip ala
nici nu neapărat elastică dar de
tip elastică în sensul că are această
formă a minus o constantă înmulțită
cu operația forța ai de ce este
proporțional cu el în acest caz
mișcarea oscilatorie se numește
armonică și are ecuațiile de dus
în minutele precedente dacă ne
uităm la definiția Constantin ca
putem observa că pulsația este
egală cu radical din cap M dar
după cum știm pulsația este de
asemenea egală cu 2 pățit ăla perioada
de și rezultă că perioada unei
mișcări oscilatorii armonice are
ecuația 2 pi înmulțită cu radical
din mpk un exemplu foarte cunoscuți
și simplu de mișcare oscilatorie
armonică e este cel cu tați al
unui pendul elastic de un pendul
elastic este pur și simplu un Resort
Deci avem un Resort de care atârnă
mă masă cu anumită greutate gem
și asupra căruia bineînțeles acționează
o forță elastică care la echilibru
are valoarea f 0 elongația sau
alungirea resortului în poziția
de echilibru notăm cu euro Dacă
dăm un mic Impuls acestui corp
atunci el va începe să o și leze
se va întinde și se va contracta
alternativ sub acțiunea unei forțe
f și vom nota cu y elongația oscilatorului
în această mișcare de oscilație
în jurul poziției de echilibru
Deci la echilibru putem scrie că
bineînțeles f 0 este egal cu greutatea
si ce implică că ca y0 este egal
cu mg în timpul oscilațiilor de
Sila oscilație sau în oscilație
avem că e forța totală Care este
egală cu suma dintre forța elastică
și greutate sumă vectorială bineînțeles
este egală cu masa ori accelerația
aceasta este principiul de bază
al dinamicii pe care îl putem scrie
această ecuație putem scrie ca
minus ca nu ții la a înmulțit cu
0 plus y de lânga ția totală la
un moment dat a resortului plus
mg este egal cu m a dar kaiserul
este egal cu mg de se simplifică
și obținem că a minus k e y este
egal cu m a ceea ce înseamnă că
a accelerația este egal cu minus
ca supra m y axis lucru această
ecuație ne spune că oscilația unui
pendul elastic adică oscilația
unui Resort vertical este oscilația
armonică a este minus o constantă
înmulțit cu y e la un Galați

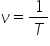
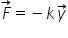
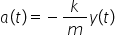
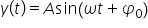 - legea mișcării;
- legea mișcării;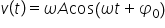 - legea vitezei;
- legea vitezei;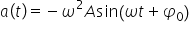 - legea accelerației.
- legea accelerației.