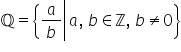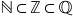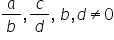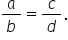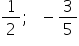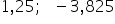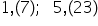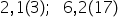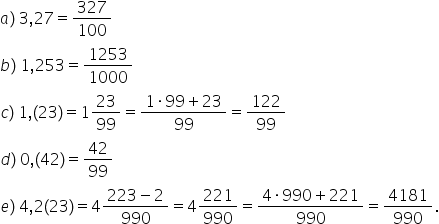Mulțimea numerelor raționale
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să definim
mulțimea numerelor raționale un
număr rațional este o pereche de
numere întregi a b scrisă sub formă
a supra b un număr rațional se
identifică cu oricare dintre fracțiile
echivalente care îl reprezintă
fracțiile a supra b și c supra
d se numesc echivalente dacă a
ori d este egal cu b ori c și o
m scrie a supra b egal cu c supra
d să dăm și un exemplu fractiile
1 supra 2 și 3 supra 6 vor fi fracții
echivalente și vom pune semnul
egal între aceste două fracții
observăm că unor 6 va fi egal cu
2 ori 3 alte cuvinte două fracții
sunt echivalente dacă au aceeași
valoare să nu uităm că linia de
fracție înseamnă împărțire dacă
un face 1 împărțit la 2 obținem
0 iar dacă efectuând 3 împărțit
la 6 obținem tot 0 așa dar aceste
două fracții sunt fracții echivalente
în continuare să vedem Ce înțelegem
prin semnul unui număr rațional
dacă numerele întregi a și b au
același semn atunci fracția a supra
b va fi egală cu modul de a supra
modul de b de exemplu fracția minus
2 supra minus 3 va fi egală cu
valoarea absolută a lui minus 2
supra valoarea absolută a lui minus
3 pe scurt scrie egal cu 2 supra
3 aici se aplică regula semnelor
învățată la operațiile cu numerele
întregi știind că atunci când împărțim
două numere întregi negative Rezultatul
este un număr pozitiv dacă a și
b 8 semne contrare atunci fracția
a supra b va fi un număr rațional
negativ de exemplu fracția minus
2 supra 3 se va scrie A minus 2
supra 3 de obicei semnul numărului
rațional se scrie în fața liniei
de fracție un definim mulțimea
numerelor raționale ca fiind mulțimea
fracțiilor de formă a supra b unde
a și b sunt numere întregi iar
b este un număr diferit de 0 să
recapitulăm puțin mulțimile de
numere învățate până acum în clasele
mai mici Ați învățat mulțimea numerelor
naturale aceasta a conține numerele
0 1 2 3 și așa mai departe mulțimea
numerelor întregi notată cu Z conține
atât numere naturale cât și opuse
le acestora adică numere de forma
minus 1 minus 2 minus 3 și așa
mai departe având în vedere că
orice număr natural sau întreg
se poate scrie sub forma unei fracții
cu numitorul unu deducem că mulțimea
numerelor întregi este inclusă
în mulțimea numerelor raționale
numerele raționale sunt fracții
de forma 1 supra 2 3 supra 7 minus
5 supra 6 și așa mai departe are
loc această relație de incluziune
mulțimea numerelor naturale este
inclusă în mulțimea numerelor întregi
care la rândul ei este inclusă
în mulțimea numerelor raționale
să vedem în continuare Care sunt
formele de scriere a unui număr
rațional numerele raționale pot
fi scrise atât sub formă de fracție
ordinară cât și sub formă de fracție
zecimală fracțiile zecimale la
rândul lor Pot fi fractii zecimale
finite sau Infinite periodice în
acest desen avem reprezentată fracția
1 supra 2 1 supra 2 este o fracție
ordinară dar dacă efectuăm împărțirea
unul pățit la 2 obținem 0 Aceasta
este o fracție zecimală finită
pentru că are un număr finit de
zecimale Așadar acest număr rațional
poate fi scris în două moduri un
alt exemplu înfășurat aici o treime
dintre un întreg aceasta este fracția
1 supra 3 Ea este o fracție ordinară
dar poate fi scris că și sub forma
unei fracții zecimale dacă efectuăm
împărțirea După efectuarea împărțirii
obținem rezultatul 0 dacă o zecimală
se repetă sau un grup de zecimale
îmi spune că ele reprezintă partea
periodică a fracției zecimale și
se pot scrie în paranteză Aceasta
este o fracție zecimală periodică
simplă pentru că partea periodică
urmează imediat după virgulă și
un alt exemplu avem reprezentată
aici fracția 1 supra 6 Aceasta
este o fracție ordinară dar dacă
efectuăm împărțirea obținem fracția
0 perioadă 6 Aceasta este o fracție
zecimală periodică mixtă deoarece
partea periodică nu urmează imediat
după virgulă observăm că înaintea
perioadei avem o zecimală aceasta
va reprezenta partea ne periodică
a fracției zecimale Așadar orice
număr rațional poate fi scris fie
sub formă de fracție ordinară fier
sub formă de fracție zecimală dacă
împărțind numărătorul la numitor
numere obții zecimală în continuare
să vedem cum putem să transformăm
fractiile zecimale în fracții ordinare
să facem câteva exemple primul
exemplu fracția zecimală 3 se poate
scrie sub formă de fracție ordinară
astfel 342 supra 800 mai exact
la numărător vom scrie Acest număr
recette inem cont de virgulă iar
la numitor punem atâtea cifre de
0 Câte zecimale avem după virgulă
un alt exemplu fracția zecimală
1 73 se va transforma în fracție
ordinară astfel 1.573 supra 1008
serbăm ca avem trei zecimale Așadar
vom pune trei zerouri să vedem
cum putem transforma o fracție
periodică unu virgulă perioada
23 se va scrie un întreg 23 supra
99 la numitor punem atâtea cifre
de 9 Câte cifre avem în partea
periodică aici respectăm calculele
introducem întregii în fracție
după Formula 1 ori 99 plus 23 supra
99 egal mai departe cu 122 supra
99 un alt exemplu 0 virgulă perioada
42 aici trebuie să scriem 0 întregi
42 supra 99 Dar vom scrie direct
42 supra 99 punctul E 1 perioada
23 avem aici o fracție zecimală
periodică mixtă se va scrie un
întreg 223 minus 2 la numărător
copiem toate zecimalele în ordinea
în care apar după virgulă apoi
scădem partea ne periodică adică
cifra 2 iar la numitor punem atâtea
cifre de 9 Câte cifre avem în partea
periodică și atâtea cifre de 0
câte avem la partea periodică egal
cu un întreg 221 supra 990 introducem
întregii în fracție 1 ori 990 plus
221 supra 990 egal mai departe
cu 1211 supra 990