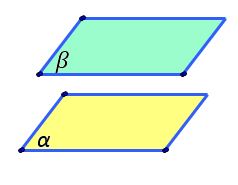
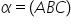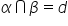Pozițiile relative a două plane (plane paralele, plane secante)

în această secvență discutăm despre

pozițiile relative a două plane

cu alte cuvinte ce așezare poate

avea un plan față de altul și putem

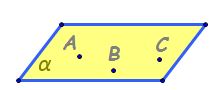
întâlni plane confundate planul

alfa coincide Iată cu planul determinat

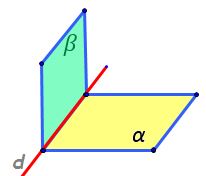
de punctele A B și C Alfa egal

cu planul abc sau putem avea plane

paralele Ce înțelegem prin plane

paralele plane care nu au puncte

în comun și am notat aici că planul

alfa intersectat cu planul Beta

este mulțimea vidă și mai putem

avea plane secante Ce înțelegem

prin plane secante și să vedem

definiția două plane se numesc

plane secante dacă intersecția

lor este o dreaptă Deci planul

alfa intersectat cu planul Beta

notăm Alfa intersectat cu Baton

de dreapta D Deci dreapta de intersecție

a planelor Alfa și Beta despre

plane paralele vom discuta mai

în detaliu când vom vorbi și despre

teoremele de paralelism în spațiu

însă Cum demonstrăm că două plane

sunt secante Păi să ne amintim

că avem această teoremă care a

fost demonstrat atunci când am

discutat despre m axiomele geometriei

în spațiu și anume Dacă două plane

distincte au un punct în comun

atunci intersecția lor este o dreaptă

ca să fie foarte clar Dacă două

plane au un punct în comun atunci

avem de fapt două posibilități

Deci avem două plane care au un

punct în comun Ce înseamnă asta

fie avem plane confundate fie avem

plane secante însă atenție când

punem condiția ca cele două plane

să fie plane distincte Deci Dacă

două plane distincte dacă trecem

aici și cuvântul distincte atunci

clar Ile nu au cum să fie plane

confundate Deci această variantă

fiică și ne rămân doar plane secante

concret ca Să arătăm că două plane

sunt secante vom arăta că ele sunt

distincte și ca un punct în comun

și acum să facem această aplicație

mi se dă cubul a b c d a prim b

prim c prim D prim și vrem să arătăm

că planele A B C și D prim c prim

c sunt plane secante Prin urmare

avem planul abc să vedem care este

să avem aici pe figură a b c Deci

avem acest plan și planul D prim

c ce Deci avem D prim c prim a

d să trasăm c d prim c prim c bun

cu alte cuvinte avem acest plan

trebuie să arătăm că aceste două

plane sunt plane secante Păi ce

avem de făcut Trebuie să arătăm

că ele au un punct în comun și

că sunt plane distincte Păi e clar

Care este punctul pe care îl au

în comun se vede foarte ușor pe

figură e să trecem așa că punctul

c aparține intersecției planelor

A B C și D prim c prim c știind

că planele sunt distincte planul

a b c este diferit de planul D

prim c prim si pentru că iată nu

are cum ca ele să fie plane confundate

pentru că planul ABC e de fapt

la anul a b c d acest plan cu verde

este planul D prim c prim c d de

ce acesta și cum avem aici un cub

înseamnă că ele sunt întradevăr

plane distincte cum avem două plane

distincte care au un punct în comun

înseamnă că ele sunt plane secante

Deci avem că planele A B C și D

prim c prim c sunt plane secante

următoarea cerință Să arătăm că

planele a prim b c și d prim c

prim b prim sunt plane secante

și avem aici planele a prim b c

a prim d c l și h om bun și planul

D prim ce prim b prim Deci avem

așa de prim c prim D prim trebuie

să arătăm că a două plane sunt

plane secante punctul lor de intersecție

nu Este evident cum a fost în exercițiul

anterior însă Haide să notăm mai

întâi că cele două plane sunt plane

distincte deci a prim d c este

diferit de planul D prim c prim

b prim iar dacă ele ar coincide

atunci asta înseamnă că punctul

c aparține planului D prim c prim

b prim ceea ce e fals pentru că

avem aici un cub si acum să vedem

care este punctul de intersecție

al celor două plane să găsim de

fapt un punct de intersecție al

celor două plane Păi e ușor de

văzut că planul D prim c prim b

prim este de fapt lanul de prim

c prim b prim a prim și a prim

e de fapt punctul de intersecție

un punct de intersecție de ceai

de Să arătăm că planul D prim c

prim b prim coincide cu planul

a prim b prim c prim D prim a mai

făcut asemenea demonstrații și

intru altă secvență însă dacă tot

vorbim aici de pozițiile relative

a două plane Haide să facem și

aici demonstrația și Avem așa a

prim b prim Este o dreaptă paralelă

cu d prim c prim pentru că avem

aici pătrat această dreaptă paralelă

cu aceasta prin urmare înseamnă

că le determină un plan unic De

ce există Alfa plan astfel încât

Alfa conține aceste două drepte

cu alte cuvinte conține și punctele

a prim b prim c prim și D prim

toate aparțin planului Alfa însă

oricare trei din aceste patru puncte

sunt necoliniare prin urmare și

punctele date aici și D prim c

prim b prim sunt necoliniare a

stat dacă planul determinat de

ele de Prin ce prim b prim Este

un plan unic dacă le determină

un plan și se află în același timp

și în planul alfa iar b prim D

prim și c prim sunt și în Alfa

înseamnă că ce obținem că planul

alfa trecem aici coincide De fapt

cu planul D prim c prim D prim

Unde La ce ne folosește această

informație Păi punctul a prim aparține

planului Alfa Alfa este identic

cu acest plan rezultă că a prim

aparține planului b prim c prim

b prim D prim c prim D prim și

deja problema noastră se rezolvă

atât dacă vreți Putem să scriem

în continuare ca asta înseamnă

că planele Haideți să scriem aici

că planele D prim c prim b prim

și a prim b prim c prim și D prim

coincid bun nouă ne este de folos

această informație Iată punctul

a prim aparține acestui plan deci

putem să notăm a prim aparține

planului de prim c prim D prim

punctul a prim aparține și acestui

plan a prim De ce Asta e Evident

cu alte cuvinte punctul a prim

aparține intersecției celor două

plane cam ele sunt plane distincte

Haide să copiem aici Deci rezultă

că planele D prim c prim D prim

și a prim De ce sunt plane secante

acum știm că două plane secante

au ca intersecție o dreaptă Haide

petrecem și Care este dreapta de

intersecție a acestor două plane

adică planul D prim c prim b prim

intersectat cu planul a prim De

ce Ce dreaptă vom obține Păi Haideți

să ne uităm puțin pe figură că

nu e deloc complicat planul D prim

c prim D prim este de fapt acest

plan Iată planul de prim c prim

b prim a prim chiar o să și trec

aici deci vorbim De fapt de acest

plan bun hașură maici planul a

prim De ce este de fapt acest plan

a prim b prim c d Deci avem acest

plan Păi Care este dreapta lor

de intersecție este dreapta a prim

b prim Da e să trecem aici că avem

de fapt dreapta a prim b prim