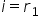Principiul Huygens. Legile reflexiei undelor mecanice.

în cea de a opta Lecție despre

oscilații și unde mecanice vom

prezenta principiul cu weekend

și apoi vom discuta despre reflexia

și refracția undelor mecanice principiul

huygens spune că fiecare punct

dintre un front de undă poate fi

considerat sursa unde lor sferice

secundare care se propagă în toate

direcțiile cu viteza de propagare

a fazei undelor în mediul considerat

Haideți să vedem ce înseamnă el

concret și mai ales cum poate fi

el folosit Deci 1 aplicabilitatea

principiului hooligans se referă

la mecanismul de generare a unui

nou front de undă plecând de la

un front de unde dat Adică dacă

știm Care este frontul Unde La

un moment dat a și dorim să aflăm

cum arată Care este geometria și

poziția frontului de undă la momentul

Terrier Delta t m t plus Delta

t principiul huygens ne spune că

trebuie să construim înfășurarea

adică suprafața tangentă a undelor

secundare cu sursa pe frontul de

undă dat adică cel de la momentul

te Haideți să vedem concret Cum

se folosește principiul huygens

pentru construirea noilor poziții

ale și geometrie ale fronturilor

de unt vezi Să considerăm o undă

sferică Deci avem o punctul roșu

în centru de unde pleacă o undă

sferică care se propagă spre exterior

generând frontul de undă concentrice

suprafețe de un drum și deci frontul

de undă va fi și el sarac și dori

să aflăm care este forma și poziția

noului freundin de la un moment

te plus Delta t dacă forma și poziția

frontului de undă la momentul t

este acest cerc Deci cunoaștem

acest cerc sau sferă în trei dimensiuni

și Dorin să aflăm cum anume se

formează frontul de undă ulterior

lui Deci principiul huygens spune

că pe acest fond de 1 dăm în fiecare

punct al lui considerăm un sus

De unde sferice secundare care

se propagă în toate direcțiile

cu aceea viteza de propagare adică

avem o astfel de situații deci

pe fiecare punct de pe frontul

de undă de la momentul t de Vino

sus Deci un punct roșu în sine

și din acest punct roșu pleacă

o undă sferică bineînțeles în toate

direcțiile din nou toate punctele

de pe frontul de undă devin surse

Deci dacă considerăm un alt punct

de exemplu acesta și el va genera

un undă sferică ce se propagă în

toate direcțiile pentru a găsi

noul front de undă construim înfășurarea

adică suprafața tangentă la toate

aceste mici sfere și ea va fi noul

sunt de unt Deci sfera sau în doi

În două dimensiuni Cum vedeți dumneavoastră

pe ecran cercul cu culoare albastră

deschisă este înfășurarea suprafața

tangentă la toate aceste noi fronturi

de undă secundare ia va fi frontul

de undă al unde e noastre la un

moment ulterior te plus de el tot

A deci aceasta este felul practic

prin care principiul huygens poate

fi folosit pentru a genera un nou

front de un de în cazul unde sferice

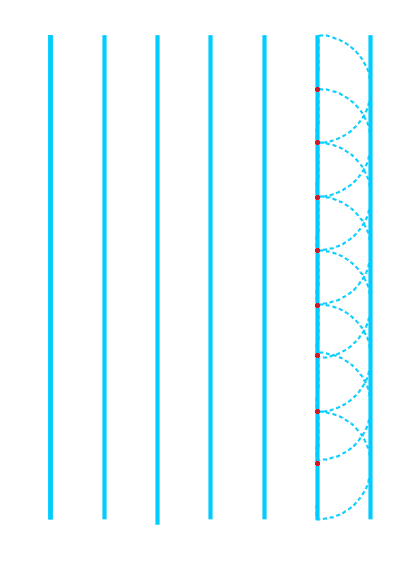
Haideți Să considerăm celălalt

caz important pe col am discutat

cel al unei Unde planici wanda

plenum este o forma unei unde toți

sferice dar la o distanță foarte

mare de sursă după cum am discutat

în lecțiile trecute Deci aceasta

este sus și acestea sunt suprafețele

de un de la îndepărtați sau la

timbi mari de propagare și știind

forma frontului de undă la un moment

dat A deci această ultimă linie

Care este suprafața de undă de

timp cel mai recent în propagarea

undei dorim să aflăm cum arată

sau să generăm cumva suprafața

frontului de undă la un moment

ulterior te plus de el tot a folosim

principiul huygens deci pe acest

front de undă luăm toate punctele

le Considerăm surse ale unor unde

sferice secundare după cum vedem

Deci toate punctele frontului de

undă devin surse ale unor unde

sferice secundare și apoi construim

înfășurat Oare acestor unde sferice

secundare notat desenate cu linie

întreruptă și ea va fi noul stadion

de înfășurarea de suprafață atentă

la toate acestea mici cercuri este

tot o linie dreaptă în două dimensiuni

sau în trei dimensiuni un plan

și el va fi noul front de undă

a lui Andi noastre originale Chiar

sista este felul în care principiul

lui huygens este folosit în practică

pentru a genera geometria frontului

de undă au unii unde oarecare să

trecem la reflexia undelor mecanice

reflect despre reflexia undelor

am discutat în lecțiile de optică

geometrică și ați făcut și dumneavoastră

în clasa a noua folosind noile

cunoștințe despre proprietățile

undelor precum faptul că ele sunt

de fapt unde plane nu sunt raze

de lumină Cum discutam în Optica

geometrică Deci am făcut câțiva

pași înainte în descrierea caracteristicilor

undelor și folosind de asemeni

principiul cu indience de data

aceasta vom putea demonstra legile

reflexiei reflexie și refracție

pornind cu reflexia Deci ce știm

este că de fapt o rază este o undă

și dacă un da sau frontul de unde

este suficient de departe de susan

Deci ne aflăm în cazul în care

sursa este undeva departe atunci

putem considera suprafețele de

undă plane Deci ne aflăm în cazul

undelor plane și avem unde incidentă

acum a cărei front de unde este

segmentul ab lați care se propagă

către suprafața de separare dintre

două medii mici avem un mediu pe

care notăm cu negru 1 și mediul

2 iar această linie albă groasă

este suprafața netedă de separare

între cele două medii și Deci unde

a noastră se propagă una noastră

plană se propagă către această

suprafață de separare după cum

am discutat Când am deschis folosire

a principiului weekend felul în

care generăm noile Unde este întotdeauna

același Considerăm fiecare punct

de pe frontul de undă de la un

moment dat ca o sursă de unde secundare

și construim tangenta la această

la aceste unde secundare sau înfășură

toarea și această înfășurat oare

va fi noul front de undă care se

va mișca și el în aceeași direcție

cu aceeași viteză bineînțeles procedând

în felul acesta banda se propagă

din aproape în aproape până ajunge

în contact cu suprafața de separare

De ce ajunge în poziția a 1 b 1

în acel moment exact același lucru

se întâmplă fiecare punct de pe

frontul de undă nou adica 1b 1D

vine o sursă de unde secundare

și Deci din fiecare punct construim

la fel aceleași mici unde secundare

diferența este că în punctul b

1 un da se deplasează în aceeași

direcție cu viteza v1 Deci notăm

cu V1 viteza de deplasare Unde

în mediul 1 în punctul A 1 on the

reflectată se va deplasa În ciuda

reflecta secundară se va deplasa

în noua direcție la fel se întâmplă

cu toate punctele de pe frontul

de undă Pe măsură ce ele ajung

în contact cu suprafața de separare

se vor deplasa în direcția unde

e reflectate notând cu m unghiul

de incidență adică unghiul dintre

fasciculul sau în Da incidentă

și normală la suprafață de separare

Deci Linia punct întreruptă este

dreapta perpendiculară în punctul

la 1:00 pe suprafața de separare

și cu aer 1 unghiul de reflexie

adică unghiul dintre un duh reflectată

și aceeași normală putem să calculăm

relația dintre e și R1 folosind

proprietățile undelor incidente

și reflectată dăduse din principiul

Hulya să notăm cu timpul în care

un de plane incidentă parcurge

B1 B1 prim De ce notăm cu de timpul

necesar aceste unde secundare să

parcurgă distanța dintre b 1 și

b 1 Prime raza incidentă secunda

raza secundară emisă din A1 în

acest timp este egală cu v-1 T

Deci dacă notăm cu a r raza unde

e secundare în în timpul în care

una secundară din de unul a ajuns

în B1 prim ia va fi egală cu v-1

t pentru că un da reflectată are

aceeași viteză de propagare ca

și unde ai incident Deci ele vor

aceste două unde un da din B1 și

unde Adina 1 cea din b unul fiind

încă partea unde incidente și cea

dinăuntru nu fiind parte de un

duh reflectată au aceeași viteză

de deplasare în concluzie B1 B1

Prime va fi egal cu a 1 A1 prim

și egal cu b 1 t din nou pentru

că cele două unde se deplasează

cu aceeași viteză fiind în același

mediu dar taurete acestui fapt

putem scrie că triunghiurile A1

A1 prin B1 prim A1 A1 prinde unul

prin și a1 b1 B1 prim sunt congruente

deoarece au două laturi egale și

două unghiuri egale laturile egale

sunt următoarele a 1 b 1 prin ca

latură comună este latura atât

în A1 A1 prin B1 prin cât și în

a1 b1 B1 prim alte două laturi

care sunt egale sunt acestea doua

despre care am vorbit Deci A1 A1

prim este egal cu B1 pe unul prim

și de asemeni unghiurile egale

sunt unghiurile drepte zici aceste

două unghiuri sunt amândouă de

90 de grade pentru că frontul de

undă fiind o undă plană este perpendicular

pe viteza de propagare a undei

această definiție de bază unde

plane Deci această această linie

este perpendiculară pe viteza undei

pe direcția deplasarea undei incidente

Iar acest fond de undă A1 plimb

pe unul prin este și el perpendicular

pe viteza de propagare a undei

reflectate pe direcția undă reflectate

de cele două unghiuri sunt de 90

de grade în concluzie cele două

triunghiuri sunt congruente iar

principala consecință este că unghiurile

b 1 a1 b1 prim și un și unul prin

B1 prin a 1 sunt egale Deci acestui

unghi este egal cu acestui dar

acestui unghi este unghiul e iar

acestui unghi este unghiul R1 deoarece

axele lor sunt perpendiculare dacă

ne uităm la dreptele ce Delimitează

unghiul B1 a 1 pe 1 prim observăm

că primul este perpendicular pe

această axă Deci a1 b1 este perpendicular

pe a A1 și de asemeni a1 b1 prim

este perpendicular pe normal în

concluzie acest unghi este egal

cu acestui și ele sunt prin definiție

unghiul de incidență din exact

aceleași motive acestui unghi este

egal cu acest unghi Și de ce Gal

cu eroul A1 prin B1 prim este perpendicular

pe direcția unde e reflectate și

a1 b1 prin este perpendicular pe

normal În consecință putem deduce

prima lege a reflexiei undelor

de acelea doua lege a reflexiei

undelor care spune că unghiul incident

este egal cu unghiul reflectat

De ce este egal cu eroul prima

lege a reflexiei undelor spune

că un de incidență și un da reflectată

sunt coplanare cu normal altfel

spus toate sau ambele unde incidente

și reflectată sunt normale și coplanare

pe suprafață de separare alte proprietăți

importante ale reflexiei unde lor

sunt următoarele reflexia nu modifică

pulsația Deci pulsația unghii unde

incidente este egală cu pulsația

Andi reflectate de aici rezultă

că și perioada și frecvența celor

două Unde vor fi egal pentru că

perioada și frecvența sunt direct

legate de pulsație Și de ce le

vor fi egal la fel lungimea de

undă a celor două unul este egal

Landa incident este egal cu London

reflectat o altă proprietate importantă

care se observă experimental este

următoarea că reflexia unei unde

mecanice la suprafață de separare

dintre un mediu elastic și un mediu

mai rigid are loc cu pierdere de

semiunda și cu schimbare de fază

cu piragia Ce înseamnă asta și

cum poate fi văzută experimental

această proprietate foarte simplu

Spre exemplu cu următorul experiment

Să considerăm coarda elastică în

care se propagă un pur și simplu

cu mâna producem cu altul unde

prin coarda elastică și această

coardă este atașată de un perete

dar atașată murdarica atașată printul

inel ce se poate mișca fără frecare

sau cu frecări minime și de ciuda

se propagă către perete și la un

moment dat ajunge aproape de perete

și atunci datorită faptului că

inelul este mobil ea a forma un

De ce ridică inelul în sus care

apoi se reflectă înapoi inelul

coborând și un da reflectând USA

înapoi în direcția opusă variația

fazei în procesul de reflexie care

prin definiție este fi reflectat

minus fi incident în acest proces

este zero Deci în acest caz în

care un de unde i se permite să

se propage II inclusiv la contactul

cu peretele nu are loc o variație

de fază și în concluzie nu are

loc o variație de lungime de unda

în procesul de reflexie vă reamintesc

Delta fi este egal cu ca Delta

Air Deci Delta fii este egal cu

2 pi pe Lambda Delta aer Deci dacă

Delta este 0 și Delta este 0 Să

considerăm alt caz Considerăm aceeași

coardă cu o undă propagând în Se

prindea către un perete dar de

data aceasta în loc să avem un

inel mobil avem o legătură fixă

Deci legăm coarda de perete Și

de ce El nu se mai poate mișca

ce se întâmplă este că în momentul

în care unde ajunge la punctul

fix ea se oprește ceea ce înseamnă

că energia cinetică a unde se transformă

într o energie potențială de tensiune

în această legătură și apoi această

energie potențială din legătură

se transformă din nou în energie

cinetică și unde a va fi reflectată

înapoi Dar acest lucru are loc

în sens opus Deci un da reflectată

va avea o viteză husa bineînțeles

dar avem are loc o pierdere de

fază egală cu pi Deci fi reflectat

faza reflectand reflectate minus

fază unde e incidente este egală

cu 180 de grade după cum se vede

din acest în acest desen care reprezintă

ceea ce observăm experimenta o

pierdere de fază sau schimbare

de fază cu pira dihanie mitico

pierdere de semiunda datorită acestei

relații Deci dacă înlocuim Delta

și ocupi în această relație observăm

că Delta Air este egal cu Lambda

pe doi Deci în cazul în care un

duh reflectată are loc între sau

reflexia are loc între două medii

în care mediul 2 este mai rigid

decât mediul 1 din care vine Unde

Aici denti avem acest fenomen de

pierdere de Sami undă și schimbare

de fază cu pi radiani sau 180 de

grade la reflexii