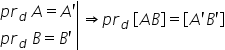Proiecţii ortogonale
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să vorbim despre
proiecții ortogonale Pe o dreaptă
și o să încep cu o definiție proiecția
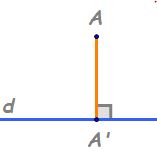
ortogonală a unui punct Pe o dreaptă
este piciorul perpendicularei duse
din acel punct pe dreaptă dacă
avem un punct A situat în exteriorul
unei drepte d și ducem prin a o
perpendiculară pe dreapta d atunci
proiecția punctului a pe dreapta
d va fi punctul a prim în cazul
în care un punct este situat pe
dreapta atunci proiecția acestui
punct va coincide cu punctul respectiv
pentru proiecția punctului a pe
dreapta d în folosi această notație
iar proiecția punctului m pe dreapta
d coincide cu punctul M deoarece
punctul m este situat pe dreapta
d o altă definiție proiecția unei
figuri Pe o dreaptă este înălțimea
proiecțiilor punctelor pe acea
dreaptă avem o figură geometrică
EF și proiect în toate punctele
acestei figuri pe dreapta d iar
unii proiecțiile acestora se obține
segmentul ab adică porțiunea mov
de pe dreapta d proiecția figurii
geometrice f pe dreapta d este
segmentul ab o să vedem în continuare
Ce înțelegem prin proiecția unui
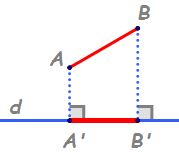
segment Pe o dreaptă proiecția
ortogonală a unui segment a b Pe
o dreaptă d este segmentul a prim
b prim unde a punctele a prim și
b prim sunt proiecțiile ortogonale
ale punctelor a și b pe dreapta
d proiecția ortogonală a unui segment
poate fi un segment sau un punct
în primul pas proiecția segmentului
AB pe dreapta d este segmentul
a prim b prim deoarece proiecția
punctului a pe dreapta d este punctul
a prim iar proiecția punctului
b pe dreapta d este punctul B prim
un indicele două proiecții se obține
proiecția segmentului AB pe dreapta
d iar aceasta va fi segmentul a
prim b prim în cazul în care Segmentul
ab este situat perpendicular pe
dreapta d atunci proiecția acestuia
a fi un punct în acest caz am notat
proiecția segmentului a b pe dreapta
d cu punctul a prim o să vedem
în continuare câteva proprietăți
Dacă dreapta AB este paralelă cu
dreapta d atunci proiecția ortogonală
a segmentului AB pe dreapta d este
un segment congruent cu AB observăm
că în acest caz Segmentul ab este
congruent cu segmentul a prim b
prim iar în cazul în care dreapta
AB nu este paralelă cu dreapta
d atunci proiecția ortogonală a
segmentului AB pe dreapta d va
avea lungimea mai mică decât lungimea
segmentului AB observăm Așadar
că lungimea proiecției unui segment
este cel mult egală cu lungimea
segmentului respectiv o să facem
în continuare o aplicație avem
un triunghi dreptunghic ABC cu
măsura unghiului A de 90 de grade
iar în acest triunghi am duce o
perpendiculară ad pe dreapta BC
laturile ab și ac se numesc catete
iar latura care se opune unghiului
drept adică BC Se va numi ipotenuză
să vedem în continuare câteva proiecții
la punctul a o să scriem proiecția
punctului a pe dreapta b c având
în vedere că AD este perpendiculară
pe b c proiecția punctului a pe
ipotenuză a fi punctul d la punctul
b să scriem proiecția punctului
b pe dreapta AC având în vedere
că b a este perpendiculară pe AC
proiecția punctului b pe dreapta
AC a fi punctul a la punctul c
o să scriem proiecția punctului
C pe dreapta ab piciorul perpendicularei
duse din punctul C pe cateta AB
este chiar punctul a la punctul
de o să aflăm proiecția catetei
ab pe ipotenuza BC vă reamintesc
că proiecția unui segment Pe o
dreaptă se obține un int proiecțiile
extremităților acelui segment de
dreaptă proiecția punctului b pe
dreapta BC este punctul B deoarece
acesta aparține dreptei BC iar
proiecția punctului a pe dreapta
BC este punctul d un int cele două
proiecții obținem segmentul BD
la punctul E o să aflăm proiecția
catetei AC pe ipotenuza BC proiecția
aceste catete pe ipotenuză va fi
segmentul DC pentru că proiecția
punctului a pe ipotenuză este punctul
d iar proiecția punctului C pe
ipotenuză este punctul c în ind
punctele d și c obținem segmentul
de ce s proiecția segmentului ad
pe ipotenuza BC având în vedere
că AD este perpendiculară pe BC
proiecția acestui segment va fi
un punct și anume punctul d proiecția
ipotenuzei BC pe cateta a b proiecția
punctului b pe dreapta a b este
punctul b iar proiecția punctului
C pe dreapta ab este punctul A
astfel proiecția ipotenuzei b c
pe cateta ab va fi tocmai cateta
ab H aflăm proiecția catetei ab
pe cateta AC având în vedere că
ab este perpendiculară pe AC deoarece
măsura unghiului a este egală cu
90 de grade proiecția segmentului
AB va fi un punct și anume punctul
a și ultimul punct aceasta o să
vă rămână temă