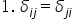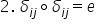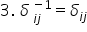Proprietăți ale transpozițiilor

în acest videoclip va mai fi Dan

ția câteva proprietăți ale transpozitiilor

știm deja cu o transpoziție este

un caz particular de permutare

și anume dacă Delta e z este o

permutare de grad n Delta Asia

are reprezentarea lui unei corespunde

1 lui 2-a corespunde doi lui Emi

nu sunt nu îi corespund e minusul

nu lui II corespunde j lui e plus

unu îi corespunde e plus 1 lui

k e corespunde k lui j a minus

unu îi corespund deja minus unu

lui corespund a lui J plus unu

e corespunde ia tui.nl corespunde

tot cu alte cuvinte fiecărui element

de corespunde el însuși cu excepția

elementelor a și z astfel încât

lui i corespund deja iar lui J

corespunde e din definiția transpoziție

y obținem o prima proprietate și

anume că Delta este egal cu Delta

j e să încadrăm această proprietate

și să notăm cu B1 Ce se întâmplă

când compunem o transpoziție cu

ea însăși să calculăm imaginile

Delta e g compus cu Delta E J conform

definiției compunerii a două funcții

va fi egal cu Delta i j de Delta

i j de I adică Păi Delta Asia de

Est i j adică Delta Asia DJ iar

Delta a j d j este adică e delta

l g compus cu Delta j d j o să

fie Delta a j de Delta IJ DJ adică

Delta e jdj delta i j DJ lui îi

corespund A deci Delta i j vrei

dar Delta i j d e este Delta compuse

cu Delta DJ aplicat unui k este

Delta i j de Delta i j de K de

K e corespunde k Deci este Delta

i j d k adică exact k oricare ar

fi k diferit de y și k diferit

de z obținem următoarea proprietate

și anume că Delta i j compuse cu

Delta Asia este părea identică

sau scrise altfel Delta EJ la pătrat

este permutarea identică reținem

o a doua proprietate și o notăm

cu pe 2 pornind de la egalitatea

Delta in j la pătrat egal cu e

o transpoziție este o permutare

adică este o funcție bijectivă

și în consecință există transpoziția

inversă Înmulțind la stânga în

această egalitate cu inversat trans

poziției Delta Asia am obține următoarea

egalitate Delta inversa Trans poziției

deja mult cu Delta l la pătrat

este egal cu intersecției Delta

i j ori permutarea identică adică

acest produs este egal cu poziția

Delta Asia iar în dreapta Egalității

avem inversa transpoziție y Delta

Asia obținem astfel următoarea

proprietate și anume că inversa

transpoziție Delta Asia este egal

cu transpoziția însăși această

proprietate o notăm cu b3 Câte

transpozitii de grade in există

deoarece Delta este egal cu Delta

j e numărul transpozitiilor de

grade n este egal cu numărul submulțimilor

ordonate ce se pot forma cu elementele

mulțimii 1 2 respectiv en și anume

combinari de n luate câte 2 care

conform formule combinari lor este

egal cu n înmulțit cu n minus 1

supra 2 să vedem Ce legături există

între permutările de grade Ian

și transpozitiile de grade se consideră

următoarea permutare de grad 4

Sigma este egal cu 1 2 3 4 cu imaginile

4 1 2 3 aceasta egalitate o Vom

înmulțit la stânga cu transpoziția

1 pot obține ma astfel egalitatea

transpoziția a14 înmulțită cu permutarea

Sigma este egal cu 1 2 3 4 4 2

3 1 mulți cu 1 2 3 4 4 1 2 3 adică

Delta 1 4 înmulțit cu permutarea

Sigma este egal cu 1 2 3 4 1 a

corespunde 4 lui 4-a corespunde

una Deci lui Noe corespunde una

lui 2 corespunde unul lui unui

corespunde 4 lui 3 corespunde doi

doi doi corespunde tu ai lui Patri

corespunde trei deci pe 3 corespunde

trei aceasta egalitate Ova înmulțire

acum tot la stânga transpoziția

Delta 2 4 obținem astfel următoarea

egalitate Delta 2 4 înmulțit cu

Delta 1 4 înmulțit cu Ce este egal

cu 1 2 3 4 1 4 3 2 înmulțit cu

1 2 3 4 1 4 2 3 avem astfel egalitatea

Delta 2 4 înmulțit cu Delta 1 4

înmulțit cu Sigma egal cu 1 2 3

4 1 corespunde unui unui corespunde

unui 2 corespunde 4 lui 4 corespunde

doi doi trei corespunde doi doi

doi corespunde 4.004 corespunde

3003 corespunde trei ceea ce nu

este altceva decât transpoziția

trei patru rescriem acum aceasta

egalitate astfel Delta 2 4 înmulțit

cu Delta 1 4 înmulțit cu Sigma

este egal cu transpoziția 3 4 înmulțim

acum tot la stânga aceasta egalitate

cu transpoziția 2 4 obținem Așadar

Delta 2 4 la pătrat old al tau

1 4 ori Sigma egal cu Delta 2 4

Delta 3 4 Dar Delta de 4 la pătrat

este permutarea identică avem ostil

permutare identică înmulțit cu

Delta 1 4 este Delta 1 4 ori Sigma

egal cu Delta 2 4 ori Delta 3 4

înmulțim la stânga din nou cu Delta

1 4 și vom obține Delta 1 4 la

pătrat înmulțit cu Sigma este egal

cu Delta 1 4 ori Delta 2.4 și ori

Delta 3 4 Dar Delta 1.4 este permutarea

identică și în concluzie Sigma

este egal cu Delta 1 4 ori Delta

2 4 ori Delta 3 4 adică Sigma este

produsul dintre transpoziția 1.4

transpoziția 2 4 respectiv transpoziția

3:00 4:00 putem întâlni această

descompunere scrisă sub această

formă transpoziția 1.4 înmulțită

cu transport Jitia 2 4 și înmulțită

cu transpoziția 3 4 am obținut

astfel o scriere a permutări Sigma

ca un produs de transpozitii obținem

astfel cea de a patra proprietate

și anume că orice permutare de

gradient se poate scrie ca un produs

de transpozitii de grade scrierea

nefiind unică