Secțiuni paralele cu baza în corpuri geometrice
Tag-uri
Partajeaza in Google Classroom

Transcript
în continuare vom discuta despre
secțiuni paralele cu bazele în
corpuri geometrice mai întâi să
vedem Ce înțelegem prin secțiune
întru un corp geometric piatră
secțiunea întrun corp în spațiu
reprezintă intersecția dintre acel
corp și un plan și avem aici un
paralelipiped dreptunghic pe care
îl am intersectat cu planul alfa
ce am obținut în urma intersecție
adică această figură geometrică
reprezentată aici cu verde este
de fapt secțiunea în acest corp
geometric secțiunea care a rezultat
în urma acestei intersecției dintre
corpul geometric și planul alfa
și chiar să denumim această secțiune
avem un patrulater am aici cu m
n p și q ce am obținut de fapt
Ce este patrulaterul m n p q este
un paralelogram AE ușor să ne dăm
seama de ce această față a paralelipipedului
dreptunghic este paralelă cu aceasta
și când intersectăm două plane
paralele cu un al treilea plan
adică cu planul alfa aici atunci
dreptele de intersecție adică NP
și mq sunt paralele la fel se obține
și că mn e paralelă cu cupe de
ce avem aici un paralelogram bun
Dacă planul cu care intersectăm
corpul geometric respectiv este
paralel cu bazele Iată planul cu
care intersectăm corpul geometric
este paralel cu bazele chiar o
să trec aici planul alfa paralel
cu cele două baze atunci vom obține
o secțiune paralelă cu bazele și
mai întâi vom discuta despre secțiunile
paralele cu bazele în prisma știind
că paralelipipedul dreptunghic
este un caz particular de mă Deci
ce avem aici este o secțiune paralelă
cu baza cu bazele între o prismă
și secțiunea pe care am obținut
o să o notăm m n p și q este un
dreptunghi atenție acest dreptunghi
este congruent cu cele două baze
sau putem să avem o secțiune paralelă
cu bază și între o prismă triunghiulară
Iată avem aici prismă triunghiulară
Nu e neapărat să fie dreapta avem
o prismă oblică a b c a prim b
prim c prim intersectată cu planul
alfa și obținem secțiunea m n p
care atenție este un triunghi congruent
cu cele două baze Deci când vorbim
de secțiuni paralele cu bazele
între o prismă ceea ce vom obține
sunt figuri geometrice congruente
cu bazele dacă avem secțiuni paralele
cu baza în corpurile rotund a ce
avem aici un cilindru pe care dacă
îl intersectăm cu un plan paralel
cu cele două baze secțiunea obținută
este un cerc care atenție este
congruent cu cele două baze ale
cilindrului Deci cu aceste două
cercuri putem să intersectăm un
plan și cu un con sau cu un trunchi
de con atenție aici secțiunile
pe care le obținem această secțiune
și aceasta sunt tot cercuri însă
în cazul conului nu obținem un
cerc congruent cu cel al bazei
5 cele două cercuri sunt cercuri
asemenea La fel și aici când avem
un trunchi de con cercul o ținut
adică secțiunea obținută nu este
congruentă cu cercurile de la bază
și este asemenea cu cele două cercuri
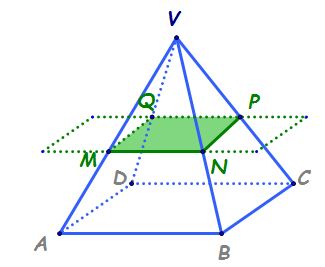
putem să avem secțiuni paralele
cu baza pentru o piramidă și avem
aici o piramidă patrulateră menea
piratka ea să fie patrulateră putem
să avem și piramide triunghiulare
dar în această situație secțiunea
pe care obținem pentru această
piramidă patrulateră regulată să
spunem ca este și regulată este
un pătrat Deci ce avem aici este
un pătrat să notăm a prim b prim
c prim D prim Deci să scriem ceva
mai jos a prim b prim c prim D
prim Este pătrat și atenție acest
pătrat este asemenea cu baza piramidei
adică cu pătratul de la baza a
b c d de vreme ce avem figuri geometrice
asemenea înseamnă că avem o egalitate
de rapoarte astfel a prim b prim
supra ab este egal cu palme avea
un alt raport aici și anume b prim
c prim supra b c egal mai departe
Cu ce prim deprim Deci acest segment
supra CD egal mai departe și cu
a prim D prim supra Ade și nu e
neapărat nevoie să ne oprim aici
egal mai departe cu v a prim supra
va egal mai departe și cu v b prim
supra b egal cu bc prim supra BC
și bd prim supra vede Deci trecem
aici puncte puncte alte cuvinte
să reținem că în cazul secțiunilor
paralele cu baza entropia Meda
obținem figuri geometrice asemenea
cu bază