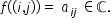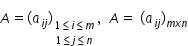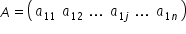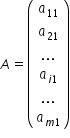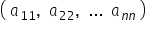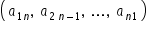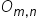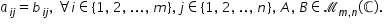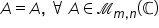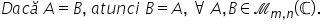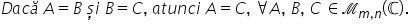Tabel matriceal. Matrice. Mulțimi de matrice

în această secțiune vom discuta

despre o noțiune deosebit de importantă

atât pentru matematică cât și pentru

celelalte științe și anume despre

Matrice cu ajutorul acestora studiem

compatibilitatea și rezolvăm sisteme

de ecuații liniare de asemenea

ele sunt utilizate în reprezentarea

transformărilor liniare în teoria

grafurilor în analiza matematică

jocurile pe calculator sunt o pasiune

pentru mulți dintre noi Dar știai

că proiecția imaginilor tridimensionale

pe ecrane bidimensionale utilizează

conceptul de Matrice criptografia

utilizează pe lângă conceptul de

permutare și conceptul de Matrice

și anume În ciprul Hill mișcarea

corpurilor rigide este un domeniu

important al fizicii care utilizează

noțiunea de Matrice alături de

optică și mecanică cuantică managera

de proiecte utilizează în scrierea

proiectelor matricea cadru logic

în economie matricele sunt utilizate

pentru studiul tendințelor stocurilor

de mărfuri utilizarea profitului

și minimizarea pierderilor matricele

sunt utilizate și în spectroscopie

în genetică în robotică în teoria

jocurilor respectiv teoria controlului

algoritmul pagerank care Ordonează

paginile între căutare Google utilizează

de asemenea o categorie specială

de Matrice numită matricele stochastice

organizarea datelor în tabele ne

permite analiza și interpretarea

acestora tabelul din imagine descrie

ponderea elevilor cu rezultate

slabe la citire și lectură matematică

și Științe la Testele Pisa din

2006 2009 și 2012 comparativ cu

media în Uniunea Europeană în schimb

tabelul din această imagine prezintă

doar datele referitoare la România

la cele trei categorii organizate

pe ani astfel pe prima linie sunt

date referitoare la citire și lectură

pe linia a doua sunt date diferit

Oare la matematică iar pe linia

a treia sunt date referitoare la

științe pe coloane avem datele

organizate pe ani 2006 2009 2012

un astfel de tabel se numește tabel

matricială aici avem un tabel cu

trei linii și cu trei coloane aici

avem un tabel cu trei linii și

o singură coloană iar Aici avem

un tabel cu o singură linie dar

cu trei coloane așezarea numerelor

în tabel nu este întâmplătoare

stabilind USA de fapt o corespondență

între poziția ocupată de un număr

din tabel și valoarea acestuia

această poziție se identifică pentru

o pereche ordonată de numere naturale

care Precizează linia și coloana

j pe care se află numărul spre

exemplul 41 virgulă patru la sută

este un element care se găsește

pe linia 3 respectiv coloana 2

Deci va avea poziția 3 2 sau elementul

50 și 2 la sută se află pe linia

2 respectiv coloana 1 generalizând

obținem următoarea definiție Fie

m și n două numere naturale nenule

se numește Matrice cu m linii și

m coloane sau Matrice de tip Yemen

cu elemente numere complexe a funcției

f definită pe produsul cartezian

al mulțimilor 1 2 m respectiv 1

2 n cu valori în mulțimea numerelor

complexe astfel perechi E J îi

asociem prin funcția f elementul

a i j din mulțimea numerelor complexe

aceste elemente Ai grijă la rashad

sub forma unui tablou cu m linii

și cu m coloane astfel numerele

a j de numim elementele matricei

notată în acest caz cu litera a

această scriere este unică uneori

mai notăm matricea și astfel punând

în evidență valorile pe care le

poate lua indicele de linie respectiv

indicele de coloană alteori precizăm

doar valorile maxime pe care le

ia indicele de linie respectiv

indicele de coloană alte ori pentru

simplitate folosind doar această

notație mulțimea matricelor de

tip m n cu elemente numere complexe

se notează m indice n De ce mulțimea

matricelor de tip Yemen cu elemente

numere reale se notează m indice

m n cu elemente din Iași dacă elementele

să numere raționale atunci mulțimea

A acelor matrici se notează cu

m n p q Ia Dacă elementele să numere

întregi se notează cu m indice

m n d z cum z este inclus în q

este inclus în aer iar acesta este

inclus în mulțimea numerelor complexe

putem spune că avem și relația

m de ce include mulțimea matricelor

de tip Yemen cu elemente din care

include mulțimea matricelor de

tip MN cu elemente din q și care

include mulțimea matricelor de

tip Yam Yam cu elemente din z să

trecem În revistă câteva cazuri

particulare de matrice Dacă m este

egal cu 1 atunci matricea a este

de tipul unui an Sasa reprezentată

astfel și poartă numele de Matrice

linie Dacă n este egal cu 1 atunci

matricea a este de tipuri M1 se

reprezinta astfel și poartă numele

de Matrice coloană Dacă m este

egal cu n atunci matricea a este

de tipul n n se numește Matrice

pătratică de ordinul n și are această

reprezentare mulțimea ordonată

a11 a22 imn poartă numele de diagonala

principală a matricei a iar mulțimea

ordonată a unui an a 2n minus unu

an1 poartă numele de diagonala

secundară a matricei a suma elementelor

de pe diagonala principală a matricei

a a11 a22 plus Ionel poartă numele

de urmă matricei a și se notează

cu trece Dacă toate elementele

sunt egale cu 0 atunci Patricia

se numește Matrice nulă și se notează

cu o indice m n se consideră lemn

4 Matrice matricea a b c și d și

să precizăm tipul acestora Matrice

matricea a are o singură linie

și patru coloane elementele sale

să numere raționale respectiv iraționale

și atunci a este de tipul 1 4 cu

elemente din mulțimea numerelor

reale Matrice Audi are trei linii

și o singură coloană iar elementele

sale sunt numere întregi iraționale

respectiv complexe și atunci b

aparține mulțimii matricelor de

tipul 3 1 cu elemente din mulțimea

numerelor complexe matricea Ce

este o matrice cu două linii și

trei coloane iar elementele sale

sunt numere naturale respectiv

întregi și atunci matricea ce putem

spune că este o matrice de tipul

doi trei cu elemente din Zet matricea

de are trei linii trei coloane

elementele sale sunt numere iraționale

complex naturale respectiv raționale

și atunci matricea de este o matrice

pătratică de ordinul 3 cu elemente

numere complexe să scrie Ma acum

câteva elemente ale acestora Matrice

elementul a13 este element al matricei

și se găsește pe coloana a treia

elementul 1 4 este elementul care

se află pe linia 1 respectiv coloana

4 și este egal cu radical din 2

dacă aș dori să precizezi elementul

b21 el se găsește pe linia a doua

respectiv coloana 1 Deci este egal

cu e sau elementul b11 este un

element care se găsește pe linia

1 respectiv coloana nu deci este

egal cu 0 pentru matricea ce să

precizăm elementul c23 linia 2

coloana 3 Deci este egal cu 3 sau

elementul C12 el se găsește pe

linia 1 coloana 2 și este egal

cu minus 3 să precizăm elementul

de 2 1 că se găsește pe linia 2

coloana 1 De ce este egal cu 0 d33

îl se găsește pe linia 3 coloana

3 și este egal cu aranjamente de

3 luate câte unul din păcate urma

matricei nu se poate calcula decât

pentru matricea de pentru că doar

matricea de este o matrice pătratică

și atunci urma matricei d este

egal cu elementul a11 adică radical

din 2 plus i la puterea a doua

adică elementul ei doi doi elementul

a33 adică aranjamente de 3 luate

câte 1 este egal cu radical din

2 ep amintim că este egal cu minus

1 iar aranjamente de 3 luate câte

unul este 3 factorial supra 3 minus

1 2 factorial adică este egal cu

radical din 2 minus 1 plus 3 obținem

Așadar urma matricei de ca fiind

egală cu radical din 2 plus 2 să

vedem acum Ce înseamnă egalitatea

a doua Matrice date două Matrice

a și b de tipul mie cu elemente

numere complexe spunem că matricele

a și b se numesc egale dacă elementul

a i j este egal cu elementul b

e j pentru orice n aparținând mulțimii

formate din elementele 1 2 respectiv

m iar Z aparține mulțimii formate

din elementele 1 2 n date matricele

a și b pătratice de ordinul 2 să

determinăm parametrii a b x y și

z parametrii reali astfel încât

cele două Matrice să fie egale

ne punem problema Egalității a

doua Matrice numai atunci când

cele două Matrice au aceeași dimensiune

conform definiției matricele a

și b sunt egale dacă elementele

corespunzătoare adică elementelor

de pe aceleași poziții sunt egali

adică elementul a11 este egal cu

elementul b11 pe din aceasta egalitate

obținem faptul că 1 este egal cu

a la a doua plus Ba dar aceasta

egalitate o putem privi ca o egalitate

de numere complexe și asta înseamnă

că partea reală a numărului complex

din stânga Egalității este egal

cu partea reală a numărului complex

din partea dreaptă a Egalității

Adică 1 este egal cu a la pătrat

iar partea imaginară a numărului

complex din membrul stâng Care

este 0 este egală cu partea imaginară

a numărului complex din membrul

drept Care este b adică 0 este

egal cu b obținem așa dar faptul

că a aparține mulțimii formate

din elementele minus 1 și 1 iar

b este egal cu 0 din egalitatea

a21 este egal cu b 2 1 obținem

ecuația 2 este egal cu 2 la puterea

x minus unu dar funcția exponențială

este o funcție injectivă ceea ce

ne permite să afirmăm că unul este

egal cu x minus unu obținem dula

astfel pe x ca fiind egal cu 2

din egalitatea a1 2 este egal cu

b 1 2 obținem ecuația x minus y

este egal cu 2 dar cu mixera egal

cu 2 obținem ecuația 2-a minus

egal cu 2 ceea ce ne tesl identificăm

pe Y8 egal cu zero a mai rămas

o singură egalitate și anume a22

este egal cu B 2.2 ceea ce determina

ecuația 3 este egal cu logaritm

în baza 2 din z de asemenea funcția

logaritmică este o funcție injectivă

adică logaritm în baza 2 din 8

este egal cu logaritm în baza 2

din z și cum funcția logaritmică

este o funcție injectivă deducem

că z este egal cu 8 proprietățile

relației de egalitate matricelor

pe mulțimea matricelor de tipul

MN cu elemente din mulțimea numerelor

complexe sunt generate de proprietățile

relației de egalitate pe mulțimea

numerelor complexe astfel orice

Matrice este egală cu ea însăși

pentru orice Matrice de tipul MN

și cu elemente din mulțimea numerelor

complexe regăsim Așadar proprietatea

de reflexivitate dacă matricea

a este egală cu o matrice b atunci

matricea b este egală cu matricea

a Oricare ar fi a și b două Matrice

de tipul MN cu elemente din c Reprezintă

proprietatea de simetrie dacă o

matrice a este egală cu matricea

b și matricea b este egală cu matricea

c atunci și matricea a este egală

cu matricea a c pentru orice Matrice

a b și c de tipul MN cu elemente

din mulțimea numerelor complexe

această proprietate poartă numele

de proprietate de tranzitivitate