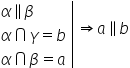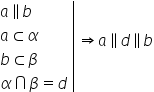Teoreme de paralelism. Aplicații
Tag-uri
Partajeaza in Google Classroom

Transcript
să facem acum câteva aplicații
folosind teoremele de paralelism
cum am spus că demonstrăm că două
plane sunt paralele pe avem această
teoremă dacă un plan conține două
drepte concurente paralele cu un
alt plan atunci cele două plane
sunt paralele Deci dacă planul
alfa conține două drepte concurente
și aceste două drepte a și b sunt
paralele cu planul Beta înseamnă
că planul alfa a paralel cu Beta
în probleme vom proceda puțin diferit
și anume ca Să arătăm că planele
Alfa și Beta sunt paralele vom
arăta că planul alfa are două drepte
concurente paralele cu alte două
drepte concurente din planul Beta
Și de aici rezultă că el fie paralel
cu Beta Păi unde sa vedem dacă
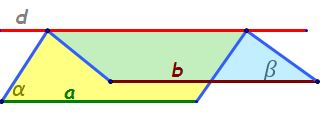
e adevărat Deci dacă avem așa dreapta
a paralelă cu dreapta d și dreapta
b paralelă cu dreapta c rezultă
oare Să scriem aici rezultă oare
Că planele Alfa și Beta sunt plane
paralele Păi Haideți să ne gândim
puțin ca să facem și legătura cu
această teoremă dacă a este paralelă
cu d dreapta Paralelă cu dreapta
d dreapta d inclusă în acest plan
venit și trece mai dreapta d inclusă
în betex Pe o dreaptă paralelă
cu o altă dreaptă dintre un plan
înseamnă că este paralelă cu planul
Deci dreapta e paralelă cu planul
Beta rezultă că a e paralelă cu
Betta acum dreapta b paralelă cu
dreapta c b paralelă cu c c este
inclusă în Betta si vom nota că
dreapta d este și ea paralelă cu
planul Beta dreapta b paralelă
cu Beta și noi mai știm că dreptele
a și b sunt drepte concurente de
a intersectat cu b și avem aici
punctul de concurență Este A păi
avem două drepte a și b concurente
care sunt paralele cu planul Beta
pe axa Ce scrie aici în teoremă
două drepte concurente paralele
cu un alt plan înseamnă că cele
două plane sunt paralele Deci din
aceste relații din aceste trei
aceasta aceasta și aceasta rezultă
că planele Alfa și Beta sunt paralele
O să vedeți că în exerciții mai
ușor să folosim această observație
decât să folosim această teoremă
Deci vom arăta că dacă un plan
are două drepte concurente care
sunt paralele cu alte două drepte
concurente dintru Norton înseamnă
că cele două plane sunt paralele
acum de ce e nevoie ca cele două
drepte c și d să fie concurentei
de Siri nu pot fi paralele sau
confundate Păi de vreme ce vorbim
de drepte coplanare c și d sunt
în același plan înseamnă că avem
doar aceste posibilități ele sunt
fie confundate confundate fie sunt
drepte paralele adică Haide să
scriu așa paralele adică ce paralel
cu d asta în situația în care ele
nu sunt drepte concurente Deci
dacă ar fi drepte paralele Haide
să vedem avem aici Ce știi e d
c și d Păi ce am obține în asemenea
situație noi avem că a este paralelă
cu d deci a paralelă cu d b este
paralelă cu c d paralelă cu c pa
Și din această relație cu ce paralelă
cu d înseamnă că dreptele a și
b sunt drepte paralele ceea ce
contrazice ipoteza noastră cum
că a și b sunt drepte concurente
la fel se întâmplă și dacă ele
ar fi confundate Deci din această
cauză se pune condiția ca cele
două drepte c și d să fie întradevăr
drepte concurente să aibă un punct
de intersecție și acum Haideți
să facem și o aplicație avem cubul
a b c d a prim b prim c prim D
prim și vrem să arătăm că planul
a prim d b este paralel cu planul
D prim b prim c Deci planul a prim
d b lungimea apoi pe d cu b pe
a prim cu b nu se vede foarte clar
că no să ne vom descurca și acest
plan Să arătăm că e paralel cu
planul D prim b prim și mai avem
punctul C unim acum d prim Cu ce
Cum facem Să arătăm că cele două
plane sunt paralele Păi trebuie
să arătăm că două drepte concurente
din acest plan sunt paralele cu
alte două drepte concurente din
acest plan și ca să identificăm
mai ușor ce drepte să folosim Cum
folosim un alt cub casă nu încărcăm
aici notația oricum nu se văd foarte
bine planele un și să găsim o dreaptă
din acest plan care să fie paralelă
cu o dreaptă din acest plan pe
dreapta d prim b prim este paralelă
cu ce dreaptă cu dreapta d care
face parte din primul plan de ce
avem paralelismul acestor două
drepte Păi d b b prim D prim Este
program de fapt el e chiar dreptunghi
însă e suficient Să arătăm că e
paralelogram ca Să arătăm că cele
două drepte sunt paralele Cum arătăm
că avem aici un paralelogram apoi
d d prim și b b prim d d prim și
b b prim sunt drepte paralele avem
un punct le segmentul d d prim
și segmentul b d prim sunt segmente
au lungimile egale d sunt segmente
congruente rezultă din proprietățile
paralelogramului că de B B prim
D prim este paralelogram și obținem
că DB este paralelă cu d prim b
prim și momentan păstrăm această
informație o subliniem pentru că
mai avem nevoie de alte două drepte
paralele una să facă parte din
acest și cealaltă din acesta Ce
drepte să alegem Păi Haideți să
șterg aici Iată dreapta ad pardon
a prim d este paralelă cu c dreaptă
cu b prim c De ce are loc această
relație de paralelism între cele
două drepte pentru că a prim b
prim c d este și el un paralelogram
de fapt și el este tot dreptunghi
însă vom scrie direct pentru că
a prim b prim demonstrația este
foarte asemănătoare cu ce am făcut
aici Cum folosim segmentele a prim
b prim și D c Deci devreme c a
prim b prim c d este paralelogram
rezultă că avem că a prim d este
ala cu b prim c și avem și această
relație am găsit aceste două relații
deci a prim d este paralelă cu
b prim c și mai avem că DB este
paralelă cu d prim D prim Cum sunt
cele două drepte cele două perechi
de drepte sunt drepte concurente
Haide să trecem aici că a prim
D Deci ce avem aici a prim b intersectată
cu d b Iată cu d b sunt două drepte
concurente punctul de intersecție
este d și b prim c este intersectată
cu d prim b prim punctul de intersecție
fiind punctul B prim din toate
aceste relații ce avem Avem două
drepte curente paralele cu alte
două drepte concurente dintre un
alt plan b c rezultă că cele două
plane sunt paralele deci a prim
d b paralel paralel cu d prim D
prim c ultima problemă este aceasta
și Alfa și Beta plane paralele
Deci Alfa și Beta sunt plane paralele
și dreptele B B prim și c c prim
intersectează planele Alfa și Beta
ca în figura dreapta b b prim intersectează
planele Alfa și Beta n b și b prim
și dreapta c c prim intersectează
în punctul C și în punctul c prim
dacă dreptele B B prim și c c prim
se intersectează în punctul A iar
Da e si punctul lor de intersecție
și b prim c prim are 20 de cm b
prim c prim chiar o să și trasăm
are 20 de cm trecem aici 20 cm
și a b supra a b prim a b supra
a b prim avem raportul 2 supra
5 trebuie să aflăm lungimea segmentului
BC adică ne interesează lungimea
acestui segment Cum să rezolvăm
această problemă vă las puțin timp
să vă gândiți Păi dreptele B B
prim și c c prim sunt drepte concurente
B B prim intersectat cu c c prim
avem punctul de intersecție a notat
în problema am are două drepte
concurente si determină determină
un plan unic Deci rezultă că există
gama plan adică planul determinat
dreptele B B prim și c c prim pun
planul gama de ce planul determinat
de aceste două drepte intersectează
planul alfa și planul Beta pe care
dreapta de intersecție a planelor
gama și Alfa Deci planul gama intersectat
cu planul alfa ce obținem pe punctul
C se află și în planul gama Da
dar se află și în planul alfa iar
punctul B la fel se află aparține
și planului gama și planului Alfa
asta înseamnă că dreapta de intersecție
a planelor Alfa știind că a ma
este dreapta BC absolut la fel
planul gama intersectează planul
Beta după ce dreaptă Păi după dreapta
b prim c prim Deci avem că planul
Gama Deci planul gama intersectează
planele Alfa și Beta după dreptele
b c b c și b prim c prim Ce știm
despre cele două plane Alfa și
Beta sunt plane paralele De fapt
ce trebuie să folosim Folosind
teorema fierăstrăului pentru că
avem aici două plane care sunt
tăiate de un al treilea plan asta
înseamnă că dreptele de intersecție
sunt drepte paralele Deci dreapta
c b paralelă cu b prim c prim rezultă
din teorema fierăstrăului că de
ce sau Ce becuri să îi spunem e
este paralelă cu b prim c prim
Deci avem că c b e paralelă cu
b prim c prim ce facem în continuare
Păi cum avem acest paralelism Ce
rezultă Păi Folosind definiția
asemănării rezultă din definiția
asemănării prescurtez astfel că
triunghiul c a b este asemenea
cu triunghiul c prim a b d și triunghiul
c a b este asemenea cu triunghiul
c prim a b prim pe asta înseamnă
că laturile acestor două triunghiuri
sunt proporționale și noi avem
nevoie de lungimea segmentului
BC mese de aici una porc și mai
avem lungimea segmentului b prim
c prim d și Problema e ca și rezolvată
rezultă Haide să scrie rapoartele
mai întâi putem să trecem laturile
triunghiului de sus a b supra va
fi egal cu AB BC și af ace și acum
să vedem ab latura AB este opusă
unghiului c care e congruent cu
unghiul c prim și unghiului c prim
se opune latura ab prim b c avem
a b supra a b prim BC iar unghiul
A e cu d c congruent cu unghiul
a d și d c avem supra b prim c
prim și na mai rămas a c prim și
acum să înlocuim noi avem nevoie
de lungimea segmentului BC bun
Deci avem nevoie de acest report
și mai cunoaștem acest raport a
b supra a b prim Deci luăm această
egalitate de rapoarte și trecem
direct rezultă 2 supra 5 egal cu
b c supra D prim c prim Este 20
de cm avem o proporție de unde
obținem că b Ce este egal cu 2
ori 20 supra 5 Deci vom obține
8 cm opt centimetri și acesta este
răspunsul trecem aici pe figură
8 cm

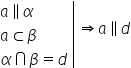
.JPG)