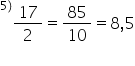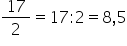Transformarea fracțiilor ordinare în fracții zecimale
Tag-uri
Partajeaza in Google Classroom

Transcript
să vedem acum Cum transformăm fracții
ordinare în fracții zecimale Dacă
ați urmărit filmulețele anterioare
atunci sigur vă amintiți că între
o secvență video făcută înainte
am discutat despre aceste tipuri
de transformări transformări de
fracții ordinare atenție cu numitorul
putere a lui 10 în fracții zecimale
poate cuvinte despre ce fel de
fracție am vorbit atunci Păi acele
fracții ordinare adică fracțiile
care se scriu cu linie de fracție
care au la numitor o putere a lui
10 adică 10 sau numitorul poate
să fie 100 sau numitorul poate
să fie 1.000 și așa mai departe
ce idee să dăm un exemplu 23 pe
10 23 supra 123 supra 1000 despre
aceste tipuri de fracții ordinare
am discutat și le am transformat
în fracții zecimale cum am făcut
Haide să ne amintim rapid 23 este
un număr natural Deci virgula lui
este după ultima cifră a Dică aici
când transformăm cu asemenea fracție
ordinară în fracție zecimală virgula
se mută spre stânga peste atâtea
cifre Câte zerouri are acea putere
a lui 10 de la numitor pe aici
avem un singur te rotești mutam
virgula spre stânga este o cifră
adică înaintea lui 3 cu alte cuvinte
vom obține 2 cât obține mai avem
23 supra 100 virgula Care este
după 3 se mută spre stânga peste
două cifre acum pentru că avem
două zerouri la numitor Deci peste
o cifră peste încă o cifră Deci
înaintea lui 2n există numărul
virgulă 23 dar există 0 iar Aici
si vom obține păi la fel numărul
23 are virgula pe trei o mutăm
spre stânga peste Una două trei
cifre o cifră două cifre Trei cifre
aici am avea virgulă Deci restul
completăm cu 0 0 23 un despre aceste
tipuri de fracții am discutat în
lecția anterioară acum vrem să
învățăm să transformăm în fracție
zecimală orice tip de fracție ordinară
de fapt cum vom proceda dacă avem
o fracție ordinară De exemplu a
supra b ca să o scriem ca fracție
zecimală Trebuie doar să îl împărțim
pe a la b pentru că linia de fracție
reprezintă operația de împărțire
Deci cum avea a împărțit la b cu
alte cuvinte în această lecție
învățăm să împărțim numere naturale
și gata prima exemplu 17 supra
2 cam Cum să scriem această fracție
ordinară ca fracție zecimală Păi
avem două variante și pe una deja
o cunoaște putem să simplificăm
sau să amplificăm această fracție
în așa fel încât la numitor să
obținem o putere a lui 10 apoi
de simplificat nu avem Cu ce să
simplificăm pentru că deja îi fracție
ireductibilă însă putem să o amplificăm
cu 5 pentru că 5 ori 2 ne dă 10
de ceartă că am obținut o fracție
cu numitorul o putere a lui 10
17 ori 5 ne dă 85 Păi 85 supra
10 ne dă 8 sau o altă variantă de
a scrie această fracție ordinară
ca fracție zecimală este de el
împărțit pe 17 la 2:00 și Haideți
să facem alături împărțirea 17
împărțit la 2 și Atenție nu facem
împărțirea cu rest românce Pepina
împărți așa cum am învățat doi
intră în unu Nu dar doi intră în
17 De câte ori de 8 ori 8 ori 2
ne dă 16 facem diferența 17 minus
16 ne dă 1 am obținut câtul 8 restul
unu continuăm acum împărțirea însă
Cum facem asta numărul 17 este
un număr natural de cel se poate
scrie în 17 ungă maici oricât de
multe zerouri nesemnificative dorim
și începem Evident prin adăuga
câte un singur 0 adăugăm primul
0 nesemnificativ am făcut scăderea
17 minus 16 mai avem ceva de coborât
Păi am ajuns în dreptul virgulei
nu vom trece virgula si o vom trece
la cât Deci 8 coborâm 0 întotdeauna
vom coborî câte un 0 ori De câte
ori este necesar 10 împărțit la
2 ne dă cinci cinci ori 210 iar
dacă deja sa încheiat împărțirea
avem 8 venim aici notăm 8 exact ceea
ce am obținut și aici pentru că
era natural să obținem același
rezultat aveam aceeași fracție
Deci Iată cum putem împărți două
numere naturale 17 împărțit la
2 alt exemplu 136 supra 25 mai
întâi fiind numere mai mari vedem
dacă putem să simplificăm această
fracție Păi 25 se scrie cinci ori
cinci Deci aici 25 se împarte exact
la 5 136 se împarte exact la 5
nu pentru că ultima cifră este
6:00 nu e nici 0 nici cinci Deci
nu putem să simplificăm această
fracție însă putem să o amplificăm
Cu cât Păi cu patru patru ori 25
ne dă 110 obținem o cu numitorul
104 ori 136 Nevada 544 scris ca
număr zecimal vom avea 5 același
lucru putem să îl facem deci putem
să transformăm 136 supra 25 și
prin împărțirea lui 136 la 25 ce
idee să facem împărțirea voi scrie
aici ca să avem loc Deci 136 împărțit
la Să scriem aici că vom avea nevoie
de 0 ori împărțit la 25 bun cum
începem pe 25 nu intră în unu nu
intră nici în 13 dar intră în 136
de câte ori Păi dacă am pune aici
Patru patru ori 25 ne da 100 Adică
noi aici trebuie să vedem Trebuie
să găsim acel număr care înmulțit
cu 25 ne dă un număr apropiat de
136 dar mai mic decât el cum am
spus dacă trecem patru palme obține
100 dacă trecem însă 5 comanda
cinci ori 25 125 dacă trecem șase
șase ori 25 de 250 e prea mare
trece 236 Deci varianta corectă
este cinci cinci ori 25 de 225
facem scăderea 6 minus cinci unu
trei minus doi unu și aici nimic
Am un restul 11 câtul 5 Ce facem
acum scrie numărul folosind zerourile
nesemnificative mă refer la de
împărțit Deci 136 virgulă zero
trecem câte un zero Am ajuns în
dreptul virgulei pentru că am făcut
scăderea însă virgulă nu o vom
trece la rast și la cât și la rest
coborâm acestea 0 110 împărțit
la 25 de câte ori intră 25 în 110
de patru ori patru ori 25 ne dă
100 venim și facem scăderea 010
0 1 minus 0 1 1 minus 1 nimic Ce
facem acum am făcut scăderea mai
avem ceva de coborât sigur putem
să mai adăugăm încă un zero nesemnificativ
pentru creată împărțirea noastră
nu sa încheiat Cum a fost aici
Deci coborâm încă un zero și avem
100 împărțit la 25 adică patru
patru ori 25 ne dă 100 și abia
acum sa încheiat împărțirea noastră
cât am obținut 5 adică exact ce
obținut se înfige așa cum era și
normal Haideți acum să revenim
la primele fracții ordinare pe
care le am discutat în ei astăzi
secvență și avem fracția 23 supra
10 de fapt vrem să facem această
împărțire 23 împărțit la 10 Păi
Haideți să vedem cât obținem să
nu uităm alături 23 împărțit la
10 pe 10 intră în 23 De câte ori
de două ori 2 ori 10 ne dă 20 obținem
restul 3 și câtul 2 continuăm împărțirea
Deci trecem virgulă la deîmpărțit
și adăugăm primul 0 nesemnificativ
am făcut scăderea am ajuns în dreptul
virgulei unde o trecem nu o scriem
la rest și la cât și acum la arest
coborâm acest 0 30 împărțit la
10 trei trei ori 10:30 iată că
sa încheiat împărțirea avem 2 exact
ceea ce obținuse Și aici avem acum
23 Deci să notăm 23 împărțit la
100 egal cu 23 împărțit la 100
proceda la fel ca mai sus însă
Ce observăm aici că avem un număr
mai mic împărțit la un număr mai
mare Păi de câte ori intră 100
în 23 de 0 ori asta vom și nota
0 ori 100 ne dă 0 și facem scăderea
23 minus 0 ne dă 23 practică avem
restul 23 și câtul 0 continuăm
împărțirea trecem virgulă și trecem
primul zero nesemnificativ Am ajuns
în dreptul virgulă scriem la cât
și la rest coborâm acest 0 nesemnificativ
230 împărțit la 100 Păi avem numărul
2 pentru că 2 ore 100 ne dă două
sute facem scăderea și obținem
30 Acum încă nu sa încheiat împărțirea
deci mai ai nevoie de încă un zero
nesemnificativ trecem aici 0 și
el Și coborâm 300 împărțit la 100
este trei trei ori 100 300 și ia
dacă am încheiat Deci am obținut
0 exact ceea ce obținut Sem și aici
următoarea împărțire 23 acum vrem
să îl împărțim Atenție la 1000
bun Păi Haideți să tot ce am notat
aici vă voi trece mai jos și vom
face această împărțire 23 împărțit
la 1000 și să vedem ce vom obține
Deci 1000 intră în 23 de 0 0 Roman
de 0 facem diferența obținem 23
trecem virgulă și primul 0 nesemnificativ
am ajuns în dreptul virgulei pentru
că am făcut scăderea virgula o
trecem la cât coborâm primul 0
230 împărțit la 1000 Tot zero zero
ori o mie pentru că 230 mai mic
decât 1000 0 ori 1000 ne dă din
nou 0 230 minus 0 ne dă 230 acum
Ai nevoie de încă un zero bun îl
coborâm și pe acesta La cât La
rest pardon 2300 împărțit la 1000
Păi avem numărul 2 pentru că 2
ori o mie de 2.000 și facem diferența
vom obține 360 nimic Mai avem nevoie
de încă un zero pentru că tot nu
se terminat împărțirea Deci Haide
să ștergem împărțirea de aici pentru
că mai e nevoie să trecem încă
un zero pe care îl vom și coborî
Deci cât avem avem trei mii împărțit
la 1000 Deci avem numărul trei
trei ore 1000 ne dă 3.000 și facem
scăderea 0 23 de 0 23 exact cât obținut
semnifice acum Toate aceste numere
care sunt aici și 2 precum și acestea
a doua se numesc numere zecimale
finite Deci 2 un număr zecimal finit
sau altfel spus cu fracție zecimală
finită De ce o numim astfel de
unde vine cuvântul finit Elsei
acest număr se numește ce numar
zecimal finit pentru că după virgulă
avem un număr finit de zecimale
nenule aici avem o singură zecimală
nenulă la fel și 0 este un număr
zecimal finit Avem două zecimale
nenule și aici avem zecimalele
023 tot așa avem un număr zecimal
finit sau fracție zecimală finită
Ce alte numere zecimale finite
am mai întâlnit 8 5 sunt ambele numere
zecimale finite pentru că după
virgulă avem un număr finit de
cifre diferite de zero aici avem
o cifră diferită de 0 ai sunt două
cifre nenule pentru că să știți
că există și numere care numere
zecimale care după virgula au un
număr infinit de cifre diferite
de zero și în această direcție
vrem să scriem ca fracție în schimb
ala fracția ordinară 25 supra 3
și ne vom ocupa de acest lucru
în următoarea secvență video și
vom vedea că de fapt acest număr
are un număr infinit de zecimale
nenule