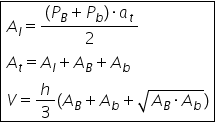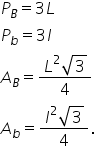Trunchiul de piramidă regulată (aplicații)

să aplicăm acum formulele învățate

pentru trunchiul de piramidă regulată

mai exact vom avea un trunchi de

piramidă triunghiulară regulată

mi se dă această piramidă triunghiulară

regulată cu înălțimea de 9 cm și

muchia bazei de 18 cm secționam

piramidă cu un plan paralel cu

baza situat la 3 cm de bază se

găsim aria totală și volumul trunchiului

de piramidă care se formează Deci

în această piramidă știind că muchia

bazei este de 18 cm de și trecem

aici ca avem 18 centimetri și mai

știm că înălțimea vo are 9 cm secționam

piramidă cu un plan paralel cu

baza situat la 3 cm de bază Deci

dacă am secționat această piramidă

cu un plan paralel cu baza acest

plan este situat la 3 cm de bază

ce ne spune acest lucru că dacă

vei intersectează acest plan în

punctul o prim atunci o prim o

are 3 cm și cu mufe o are 9 cm

înseamnă că v o prim are 9 minus

3 adică 6 cm bun și să trecem aici

să notăm și acest plan cu a prim

b prim c prim Deci trebuie să găsim

aria totală și volumul trunchiului

de piramidă a b c a prim b prim

c prim Care este formula pentru

aria totală Păi ca să găsim aria

totală avem nevoie mai întâi de

aria laterală Adică trebuie să

trecem aici Deci aria laterală

avem perimetrul bazei mici adunat

cu perimetrul bazei mari înmulțit

cu apotema trunchiului lui de piramidă

supra doi Deci avem nevoie pe lângă

muchia bazei mari și de muchia

bazei mici și de apotema trunchiului

de piramidă cum le determinăm care

ideea de rezolvare Păi când am

vorbit despre secțiuni paralele

cu baza am văzut că datorită acestei

secțiuni paralele se formează foarte

multe triunghiuri asemenea și chiar

am vorbit și de corpuri asemenea

această piramidă V a prim b prim

c prim Este asemenea cu piramida

mare și am vorbit și de raportul

de asemănare care se formează și

idee Să ne amintim pe scurt Iată

triunghiul a prim b prim c prim

Este asemenea cu triunghiul abc

un să notez aici că triunghiul

a prim b prim c prim asemenea cu

triunghiul ABC îi din acest raport

de asemănare din această relație

pardon de asemănare se formează

motoarele rapoarte și avem a prim

b prim supra ab egal cu b prim

c prim supra b c egal mai departe

și cu a prim c prim supra AC dar

și triunghiul V a prim b prim Este

asemenea cu triunghiul vab Deci

triunghiul V a prim b prim asemenea

cu triunghiul vab asta înseamnă

că raportul a prim b prim supra

ab pe care ia turn regăsim Aici

este egal 12 să trecem egal în

continuare cu v ă prim supra va

egal mai departe cu v b prim supra

vb evidentă același lucru se întâmplă

și în cazul triunghiurilor b prim

c prim asemenea v b c d a b prim

supra b b adică acest raport este

egal și un v c prim supra b c de

traci putea să putem să trecem

în continuare în v c prim supra

b c și o să trecem aici în această

parte să nu se subînțelege că din

această relație este egalitatea

cu raportul v c prim supra 10 pun

si mai avem Păi mai avem de exemplu

și triunghiul v o prim b prim asemenea

cu v o b d și triunghiul a prim

b prim asemenea cu triunghiul o

b c rezultă de aici rezultă că

v b prim supra vb adică acest raport

este egal te putem să trecem egal

în continuare cu Vio prim supra

b și o b prim supra OB egal mai

departe și cu o prim c prim supra

pardon Aici este o prim b prim

D prim b prim supra o b egal mai

departe și cu unt o prim c prim

supra o c o prim c prim supra o

c și cu o prim a prim supra o a

și mai avem probabil de și alte

rapoarte de asemănare dacă am construit

și apotema piramidei atunci o să

obținem alte două triunghiuri asemenea

știi înfund continua cu această

io cu acestea egalități notăm cu

k raportul de asemănare bun de

vreme ce avem Toate aceste rapoarte

o să ne fie destul de simplu să

găsim elementele trunchiului de

piramidă de ce Pentru că noi avem

știm Cât este vă prind și Vio cu

alte cuvinte cunoaștem acest raport

pe care chiar o să îl încerc v

o prim supra b o e un raport pe

care îl cunoaștem în funcție de

el vom găsi și celelalte elemente

ale trunchiului de piramidă momentan

să ștergem aici această relație

pe care am scris aici o vom trece

mai sus și acum am spus că avem

acest raport vei o prim supra vede

că 6 supra 9 și vrem să găsim de

exemplu muchia bazei mici a prim

b prim Unde apare a prim b prim

aici Deci avem această egalitate

a prim b prim supra a b egal cu

b prim supra vs de unde rezultă

că a prim b prim supra ab este

18 egal cu Vio prin care este 6

supra Vio Care este 6 plus 3 adică

9 Avem o proporție al determinăm

pe a prim b prim care este egal

cu 18 ori 6 supra 9 putem să simplificăm

aici și prin 9 și ne rămâne 1 și

2 2 ori 612 DC egal mai departe

cu 12 cm și venim trecem și aici

pe figura Deci am găsit muchia

bazei mici avem nevoie să determinăm

acum și apotema trunchiului de

piramidă și pentru a face acest

lucru Avem mai multe variante o

variantă este aceea de a determina

muchia laterală a trunchiului de

piramidă și atunci ca să găsim

înălțimea în trunchiul de piramidă

putem să lucrăm în plan adică luăm

separat Trapezul b c c prim b prim

cunoaștem lungimea bazei mici lungimea

bazei mari cunoaștem și aceste

lungimile muchiilor de laturilor

b prim b și c prim c e și atunci

construim înălțimea și o aflăm

o altă variantă este aceea de a

construim apotema piramidei și

pentru aceasta trecem aici mijlocul

segmentului BC nu voi mai trece

că nu voi mai hașura bem și MC

casă nu încărcăm notația construim

mediană BM care este și înălțime

pentru că vorbim de un triunghi

isoscel de ce avem aici avem bun

asta înseamnă că avem aici un unghi

de 90 de grade punctul de intersecție

al segmentului v m cu b prim c

prim trece mai notăm cu m prim

și m prim este mijlocul segmentului

b prim c prim și ce am obținut

aici chiar o să șterg aici să trecem

de pre mai aproape bun si am obtinut

aici în primul an este de fapt

apotema trunchiului de piramidă

deci putem să notăm aici apotema

trunchiului de piramidă bun Cum

facem să determinăm Păi putem să

ne folosim de triunghiurile o prim

m prim care este asemenea cu triunghiul

v o m cunoaștem raportul V oprim

suprave însă o să avem nevoie și

de lungimea segmentului BM Cum

determina lungimea acestui segment

v m p e foarte simplu În triunghiul

v om putem să aplicăm teorema lui

Pitagora pentru că triunghiul v

om este un triunghi dreptunghic

în 8 însă mai înainte trebuie să

găsim lungimea segmentului om adică

apotema bazei mari și pentru aceasta

putem să notăm că în triunghiul

ABC am mai făcut asemenea rezolvări

Care este echilateral centrul cercului

circumscris coincide cu centrul

de greutate notată c rezultă că

om are lungimea egală cu o treime

din lungimea segmentului a m Care

atenției este și mediană dar și

înălțime în triunghi echilateral

atunci dacă notăm cu l mare latura

triunghiului echilateral lungimea

înălțimii a m este egală cu l radical

din 3 supra 2 deci putem să trecem

în continuare că avem 1 supra 3

înmulțit cu l mare este 18 Deci

avem aici 18 radical din 3 pe 2

3 ori doine de 6 11 împărțit la

6 ne dă 3 Deci avem 3 radical din

3 cm și am găsit lungimea segmentului

om trece mai și 3 red cai din trei

acum ca să găsim Cât este vm avem

în triunghiul v o m măsura unghiului

O știind că este de 90 de grade

pentru că b o este înălțime d c

perpendiculară pe orice dreapta

inclusă în planul a b c d și p

o e și rezultă conform teoremei

lui Pitagora că vei m la pătrat

lungimea acestui segment este egală

cu 0 la pătrat adunat cu om la

pătrat și acum nu facem decât să

înlocuim avem la pătrat egal cu

bo este 6 cu trei adică 9 la a

doua trecem direct 81 plus om la

pătrat 3 radical din 3 la a doua

înseamnă 27 Deci obținem 108 cu

alte cuvinte vm este egal cu radical

din 108 adică și 6 radical din

3 cm și voi șterge aici O să las

doar Ultima relație și anume valoarea

lui Van bun Ce facem acum știm

Cât este vm și am spus că ne vom

folosi de triunghiuri asemenea

triunghiul v o prim m prim Este

asemenea cu triunghiul om bun ce

rezultă de aici mai rezultă că

avem această egalitate de rapoarte

și anume vei o prim supra b prim

supra b este egal cu m prim supra

vm Nu uitați noi vrem să determinăm

segmentul m prim m Știind Cât este

vm Deci avem nevoie și de bmp sigur

acest raport puteam să îl trecem

în continuare pentru piatră regăsim

v o prim supra v o fi aici și putem

să trecem și că este egal cu o

Prime în prim supra om dacă Vrem

să aflăm și pe oprim membri pun

și acum înlocuim rezultă că vei

primi este 6v este 9 Deci 6 supra

9 este egal cu b m prim supra b

m 6 radical din 3 și rezultă că

v m prin cât ne dă avem o proporție

6 ore 6 radical din 3 supra 9 avem

aici 36 împărțit la 9 4 radical

din 3 cm si am găsit Cât este vem

și cât este vem prin pe cât este

m prim m m prim m este vm minus

vm prin Deci un v m minus v m prim

egal cu 6 radical din 3 minus 4

radical din 3 adică 2 radical din

3 cm și apoi că am găsit și valoarea

apotemei trunchiului de piramidă

de ștergem aici și vom trece cât

am găsit și anume 2 radical din

3 cm acum haide să determinăm aria

laterală pentru că avem tot ce

ne trebuie deci putem să ștergem

tot ce am scris aici reținem că

vei m are 6 radical din 3 centimetri

bun cred că avem suficient spațiu

să calculăm aria laterală Care

este egală cu perimetrul bazei

mici Deci avem 3 înmulțit cu 12

adunat cu 3 înmulțit cu perimetrul

bazei mari 18 înmulțit cu apotema

trunchiului de 2 radical din 3

supra 2 și acum putem să simplificăm

pe 2:02 prin doi ne rămâne aici

unu și unu și aici vom avea așa

12 plus 18 ne dă 3390 Deci avem

90 radical din 3 cm pătrați aria

totală să trecem formula este egală

cu aria laterală plus aria bazei

mici plus aria bazei mari Cât este

aria bazei mici păi avem așa e

el mic dacă notăm aici cu l mic

avem l mic la a doua radical din

3 pe 4 Deci 12 la a doua radical

din 3 supra 4 sau Putem să scriem

12 ori 12 chiar o să scriu așa

ca să facem un calcul rapid de

2 10 ori 12 radical din 3 pe putem

să simplificăm aici 4:12 ne rămâne

unu și trei trei ori 12 36 radical

din 3 aria bazei mari să vedem

cât este o voi trece aici aria

bazei mari l mare la a doua radical

din 3 supra 4 în loc de 18 la pătrat

o să fiu tot așa 18 ori 18 ori

radical din 3 supra 4 16 m să simplificăm

pe 18 și 4 prin 2 o să ne rămână

nouă și doi la fel și aici 99 să

ne dea 81 radical din 3 centimetri

pătrați la fel centimetri pătrați

și aici rezultă aria totală Cu

cât este egală avem aria laterală

90 radical din 3 plus aria bazei

mici 36 radical din 3 plus aria

bazei mari 81 radical din 3 egal

cu avem șase cu unu șapte opt cu

311 cu 920 de 207 radical din 3

centimetri pătrați în a rămas decât

să calculăm volumul notând formula

pentru volum avem Înălțimea pe

3 înmulțit cu aria bazei mari plus

aria bazei mici plus radical din

aria bazei mari înmulțită cu aria

bazei mici 10 egal Cum sau mai

bine zis să rezultă volumul Nevada

înălțimea trunchiului de piramidă

supra 3 înălțimea trunchiului de

piramidă adică este o prim o Care

este egal cu 3 Deci avem 3 supra

3 înmulțit cu aria bazei mari 81

radical din 3 plus aria bazei mici

36 radical din 3 plus radical din

81 ori 36 și mai avem aici radical

din 3 ori radical din 3 care ne

dă 3 bun și facem acest calcul

vom obține 81 cu 36 Care ne dă

117 radical din 3 plus și vom avea

aici și 9 ori 6 deci 54 radical

din 3 obținem în final facem suma

chiar o să o trec aici 171 radical

din 3 cm cubi si astfel am de terminat

și volumul trunchiului de piramidă

De ce avem aria laterală aria totală

care ne a dat 200 7 radical din

3 și volumul 171 radical din 3

cm cubi