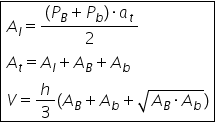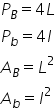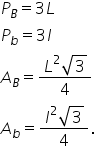Trunchiul de piramidă regulată (formule)

să te ducem acum împreună formulele

pentru aria laterală aria totală

și volumul unui trunchi de piramidă

regulată a spus și în alte secvențe

că trunchiul de piramidă se formează

prin secționarea unei piramide

cu un plan paralel cu bază și în

funcție de piramida pe care o secționam

avem diferite trunchiuri de piramidă

și acum vom vorbi de unghiul a

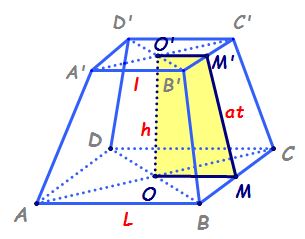
de piramidă regulată și anume avem

trunchiul de piramidă patrulateră

regulată are două baze situate

în plane paralele și bazele sunt

două pătrate asemenea Deci pătratul

ABCD este asemenea cu pătratul

a prim b prim c prim D prim și

fețele laterale Iată sunt trapeze

isoscele congruente avem patru

trapeze isoscele congruente dacă

vorbim de trunchiul de piramidă

triunghiulară regulată atunci bazele

sunt două triunghiuri echilaterale

asemenea situate în plane paralele

Fetele sunt la fel trapeze isoscele

congruente și dacă vorbim de un

trunchi de piramidă hexagonală

regulată atunci la fel bazele care

sunt situate în plane paralele

sunt hexagoane asemenea regulate

și fețele laterale sunt tot așa

trapeze isoscele să deducem acum

formulele pentru trunchiul de piramidă

patrulateră regulată aria laterală

este egală cu suma ariilor fețelor

laterale și noi știm că avem ca

fetele laterale 4 trapeze isoscele

congruente Deci avem 4 înmulțit

cu a aria unui trapez putem să

ne alegem pe oricare de exemplu

b c c prim b prim bc c prim b prim

și acum trebuie să exprimăm a aria

acestui trapez aria unui trapez

este egală cu un trecem formula

bază mică plus baza mare Deci b

prim c prim plus bc ori înălțimea

construită în acest trapez un suras

ai spațiu ca să trecem înălțimea

totul supra 2 Și acum Haideți să

construim înălțimea în o înălțime

În trapezul bc c prim b prim fie

putem să coborâm o perpendiculară

din b prim sau din ce prin pe BC

de exemplu coborâm o perpendiculară

din b prim trec aici punctul N

avem aici 90 de grade sau putem

să coborâm o perpendiculară din

oricare punct ales pe segmentul

b prim c prim taxe templu putem

să alegem chiar și mijlocul segmentului

b prim c prim în notez cu m prim

și din m prim coborâm o perpendiculară

pe BC și trec aici punctul M avem

aici 90d grade la fel și aici atenție

apotemă a unui trunchi de piramidă

este de fapt o înălțime construită

între o față laterală când vorbim

de trunchiul de piramidă regulată

oricare două apoteme sunt congruente

Deci și m prim și b prim n poate

fi considerată apotema trunchiului

de piramidă ele sunt concurente

și alegem de exemplu pe m prim

m trec aici a p apotema trunchiului

o să șterg ce am construit aici

aici Vreau să vadă că avem punctul

m și acum am construit înălțimea

o notăm cu a p t Deci venim aici

și ștergem și trecem că avem înmulțit

cu apotema trunchiului de piramidă

bun ce rezulta acum Păi vom înlocui

aria era ala este egală cu 4 înmulțit

cu în loc de aria acestui trapez

vom trece si am notat aici Iată

chiar o să copiem direct ce putem

să facem acum Păi putem să îl înmulțim

pe 4 cu fiecare termen din paranteză

în parte și atât ce vom obține

Avem așa patru ori b prim c prim

adunat cu 4 ori b c totul înmulțit

cu apotema trunchiului de piramidă

supra 2 Păi ce înseamnă 4 înmulțit

cu lungimea segmentului b prim

c prim Acum avem aici un pătrat

înseamnă că obținem chiar perimetrul

acestui pătrat de fapt perimetrul

bazei mici și patru ori b c reprezintă

perimetrul bazei mari să notăm

formula pentru aria laterală este

urmă marea perimetrul bazei mici

o să scriu așa cu b mic adunat

cu perimetrul bazei mari 130b mare

înmulțit cu apotema trunchiului

de piramidă supra doi și astfel

am găsit formula pentru aria laterală

ștergem aici ca să avem spațiu

pentru celelalte formule și acum

Care este formula pentru aria totală

e foarte simplu aria totală este

alcătuită din aria laterală plus

ariile bazelor aria bazei mici

adunat cu aria bazei mari aria

bazei mici Cu cât este egală Păi

dacă notăm latura pătratului cu

pătratului mic se spunem așa cu

l mic avem l mic la a doua aria

bazei mari dacă notăm latura pătratului

cu l mare avem l mare la pătrat

și acum lunea mai rămas să trecem

decât formula pentru volum volumul

unui trunchi de piramidă are următoarea

formulă avem înălțimea supra 3

unde înălțimea e reprezentată de

segmentul oprim o o să construim

aici Deci aceasta este înălțimea

trunchiului de piramidă înmulțit

cu ușa Cum în paranteză vom trece

aria bazei mari adunată cu aria

bazei mici adunată cu radical din

această formulă o să fie nevoie

să o ținem minte aria bazei mari

înmulțit cu aria bazei mici și

aceasta e formula pentru volumul

trunchiului de piramidă acum dacă

am vrea să trecem și formulele

pentru apotema bazei mici și apotema

bazei mari Iată apotema bazei mici

Este aceasta o prim m prim și apotema

bazei mari este o m pentru o o

prim m prim o prim m prim este

apotema bazei mici care este formula

o prim m prim Este linia mijlocie

în triunghiul a prim c prim b prim

asta înseamnă că o prim m prim

are lungimea egală cu jumătate

din lungimea segmentului a prim

b prim adică el pe 210 egal cu

al mic supra 2 la fel om Care este

apotema bazei mari are lungimea

l mare supra 2 formulele pe care

le am scris cu albastru pentru

aria laterală pentru aria totală

și pentru volum Sunt aceleași fiecăror

bim de un trunchi de piramidă patrulateră

regulată sau un trunchi de piramidă

triunghiulară sau hexagonală regulată

Deci avem aceleași formule și pentru

celelalte două tipuri de trunchiuri

de piramidă prezentate se modifică

însă ariile bazelor dacă avem de

exemplu un trunchi de piramidă

triunghiulară regulată atunci ariile

bazelor vor fi de fapt ariile unor

triunghiuri echilaterale și la

fel se modifică și calculul formulele

pentru o temă bazei mici dar și

pentru apotema bazei mari de ce

reținem aceste trei formule pentru

determinarea ariei laterale ariei

totale și a volumului unui trunchi

de piramidă regulată