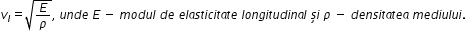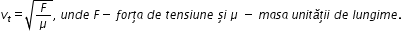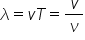Undele mecanice. Modelul undei plane.

îngeraș astea lecție destul și

la ții și unde mecanice vom discuta

despre undele mecanice și proprietățile

lor și vom introduce modelul unde

unde le mecanice sunt des întâlnite

în experiența noastră cotidiană

Spre exemplu în această imagine

vedeți undele generate pe o suprafață

de apă de o picătură de apă ce

cade pe această suprafață în desenul

schematic de sub imagine Reprezentăm

forma undelor Cum este ea a văzută

dacă Privim razant cu apa deci

da lungul suprafeței de apă unde

le sunt generate de o perturbare

ce apare în mediu Deci prima noțiune

pe care introducem este aceea de

perturbație a unui mediu care este

deplasarea unui sistem din poziția

de echilibru sub acțiunea unei

forțe externe exact cum faci această

picătură de apă care deplasează

suprafața apei între anumit punct

prin aplicarea unei forțe externe

forța datorită datorată căderii

picături mie iar această perturbații

produce o oscilație care apoi se

propagă sub formă de unde în meri

Haideți introducem noțiunea de

unda mecanică pas cu pas zici perturbații

produce o oscilație care prinde

reacția cu mediul înconjurător

cu molecule de apă în cazul acesta

produce o serie de o ții cuplate

Deci avem oscilația originală în

punctul în care se produc perturbație

inițială de către picătura de apă

în cădere și datorită intra animale

culori de apă între ele această

oscilație produsă la sursă la sursa

unde sa va transmite din aproape

în aproape sub formă de oscilații

ale moleculelor de apă înconjurătoare

surse sau perturbații inițiale

Deci avem o serie de oscilații

cuplate care se generează una din

franta în schema noastră vom avea

o serie de oscilatori verticali

adică perpendicular pe suprafața

apei care vor vor fi cuplați între

ei Deci perturbații original se

propagă prin mediu din aproape

în aproape prin cuplarea acestor

oscilatori individuali aceasta

va duce la deplasarea unde e sau

mișcarea unei și în concluzie un

de mecanică este procesul de propagare

a unei perturbații din aproape

în aproape cu viteză finită printrun

meci una mecanică din nou este

un proces când spunem unda mecanică

ne referim la un proces și anume

procesul de propagare a unei perturbații

printru mediu prin generarea unor

oscilații cuplate datorită interacțiunilor

din mediul respectiv și Deci intru

în fel un de mecanică foarte simplist

și schematic spuse este acest care

semnifică deplasarea acestor coștila

în spațiu și timp un Dan consecință

este o forma de transfer de energie

oscilatorie care are loc fără transfer

de substanță undele elastice apar

în medii în care interacția si

profa 25 de tip elastic de ceea

ce știe oscilatori care intră rând

pe rând în oscilație sunt cuplați

pentru a putea avea această transmisia

oscilației originale felul în care

ei sunt cuplat depinde de tipul

de interacție dintre elementele

Mediului în care se propagă un

da Dacă această interacție este

de tip elastic atunci un da ce

se propagă prin mediul se numește

un de elastic avem multe tipuri

de unde mecanice aceasta propagare

a unei o suprafață de apă singure

Exemplu un alt exemplu fiind o

undă sonoră de ce vedeți nacela

doare imagine este un difuzor în

în această zonă imagini avem un

difuzor care generează unde sonore

undele sonore sunt oscilații cuplate

ale moleculelor de aer undă sonoră

este un de mecanică produsă prin

vibrația diafragmei difuzorului

nostru care apoi se transmite prin

oscilațiile moleculelor de aer

să discutăm despre mărimile caracteristice

unei unde mecanice Avem două tipuri

principale de unde mecanice prima

primul tip se numește undă longitudinală

ia apare în cazul în care oscilațiile

mediului elastic au loc paralel

cu Direcția de propagare a undei

Spre exemplu comprimarea unui Resort

Deci în această schemă vedem un

Resort și dacă imprimăm dacă acționăm

cu o forță caracterizează un timp

scurt de joacă la vin spre exemplu

resortul intru în capăt vom serva

că generăm o undă care se propagă

prin Resort Deci Direcția de propagare

unde este de a lungul resortului

de asemeni însă modul în care această

un de oscilează deci oscilatorii

individuali de a lungul Unde oscilează

în paralel cu sensul de propagare

a undei De ce II vor oscila așa

orizontal acest tip de unde se

numește un dolocit Udine în care

oscilația individuală este paralelă

cu sensul de propagare a lunii

Evident celălalt caz este un dat

transversal în care o și la țiile

mediului elastică au loc perpendicular

pe direcția de propagare a undei

și un exemplu Este cel care îl

am văzut un da pe suprafața apei

Deci în acest caz picătura a căzut

un anumit punct în mijlocul destinului

nostru și apoi undele unde unde

sa propagat dar lungul suprafeței

de apă de și longitudinal Dar nu

cu suprafețele apă dar oscilatorii

individuali oscilează perpendicular

pe suprafața ei Deci aceasta acest

tip de unde se numește unda transversală

se numește lungime de undă distanța

parcursă de undă în timp de o perioadă

ca și comentariu toate celelalte

mărimi caracteristice oscilațiilor

precum pulsația oscilației frecvența

sau perioada oscilației sunt mărimi

caracteristice și pentru undă pentru

că în final o undă este un set

de oscilații cuplate în propagarea

lor Deci mărimile caracteristice

unei oscilații sunt caracteristicii

și pentru un de în plus mai introducem

și această mărime caracteristică

suplimentară pentru Honda și anume

lungimea de undă Care este din

nou distanța parcursă de un de

timp de o perioadă viteza În consecință

viteza de deplasare a unei Unde

este datorită acestei definiție

gală cu lungimea de undă împărțită

la perioadă Sau dacă vreți lungimea

de undă înmulțită cu frecvența

nu cele două tipuri de unde longitudinală

și transversală au formulele lor

pentru viteza de deplasare a undei

Deci în cazul unei unde longitudinale

prințul media lastic cu modulul

de elasticitate e și densitatea

ro viteza este radical din modulul

de elasticitate sau modulul Young

despre care am discutat în lecțiile

despre elasticitate din mecanică

împărțit la densitatea Mediului

în cazul undelor transversale prin

solid bineînțeles din nou solid

elastic viteza undelor transversale

este radical din forța de tensiune

în punctul respectiv în care calculăm

viteza împărțită la densitatea

liniar adică densitatea pe unitate

de lungime a meciului să trecem

acum la modelul unde e plane să

introducem câteva noțiuni să te

descriu forma unei unde și apoi

să definim un plan se numește suprafață

de un de suprafața Ce conține toate

punctele atinse de o undă în același

moment te deci pur și simplu avem

pentru o în de 100 cm o sursă Unde

se produce perturbatia Inițială

care apoi se propagă prin mediul

înconjurător Bineînțeles că forma

acestea unde care se propagă poate

să fie oarecare în principiu pentru

că mediul prin care se propagă

reacționează în diferite puncte

în mod diferit la un dar ce se

propagă prin el pot apărea forțe

rezistive care să încetinească

un da întru anumită regiune pot

apărea reflecții sau refracție

care se schimbă și ele forma unde

e niciunde care se propagă poate

avea în general orice formă și

se numește suprafață de un de forma

Unde La un moment dat a socotit

sau Calculați sau măsurat din momentul

în care unde a fost produsă de

perturbatia inițial în cazul particular

în care mediul de propagare este

omogen avem următoarele proprietăți

pe care le vom explica folosind

această schemă ca și comentariu

De multe ori se folosește sintagma

omogen și izotrop dar în cuvântul

izotrope sau proprietatea de izotropie

este implicată în proprietatea

de omogenitate adică un mediu omogen

înseamnă un mediu care are aceleași

proprietăți În toate punctele indiferent

de poziția la în care ne aflăm

în mediu proprietățile toate proprietățile

sunt identice izotropie înseamnă

proprietăți independente de Direcția

față de un punct în particular

izotropie a înseamnă că plecând

din punctul plecând din punctul

lui de a avut loc pentru bărbați

original plecând de la sus sau

unde a în orice direcție avem aceleași

proprietăți De ce vident dacă avem

proprietatea de mediu omogen atunci

avem și proprietatea de izotropie

revenind dacă un medie este omogen

avem următoarele proprietăți ale

unde ce se propagă prin iar în

primul rând pulsația unde va fi

uniformă Deci în orice poziție

neam afla Omega de x y z Iza grec

și z este o constantă are aceeași

valoare în orice poziție nem afla

atunci rezultă că faza un de la

un moment dat care este prin definiție

omega-3 plus fi 0 unde a fi 0 este

faza Unde la sursă la producere

este uniformă modalitatea prin

care faza Nu ar fi uniformă ar

fi dacă Omega ar avea o dependență

depozit dar dacă mediul este omogen

nu avem o dependenții de poziție

și atunci Această fază la un moment

dat A deci pe o suprafață de undă

va avea aceeași valoare nici punctele

suprafeței de unde oscilează în

față Bineînțeles că geometria suprafeței

de undă va fi sferică precum vedem

în această imagine pentru că dacă

mediul este omogen atunci viteza

de propagare este uniformă dar

distanța la care se află un an

de forma Unde rdt este el la momentul

t este plin definiții viteza ori

timpul iar Dacă viteza nu depinde

de poziție csy și zet înseamnă

că la un moment dat a raza este

o constantă ceea ce înseamnă că

un da este sferică sau în Unde

În planul ecranului Cum o vedem

noi aici este circular Deci în

concluzie întrun mediu de propagare

omogen o undă va avea formă sferică

cu suprafețele de undă fiind sfere

concentrice care cresc în rază

Pe măsură ce timpul te de propagare

crește și toate punctele de pe

o suprafață de undă se află în

faza adică fii de te faza oscilației

oscilatoarelor individual este

aceeași Deci dacă Considerăm doi

oscilatori de pe aceeași suprafață

de undă ivor avea același videt

se numește front de undă suprafața

de undă cea mai îndepărtată de

sursa unt Deci dacă vreți suprafață

de unde se conduce un care este

în fața undei în cazul desenului

nostru frontul de undă ar fi suprafața

de undă în albastru cea mai îndepărtată

de sursă și în consecință lungimea

de undă Lambda care va duc aminte

este viteza mulți tool cu perioada

va fi distanța dintre două suprafețe

de un De ce corespund aceluiași

moment de oscilație Spre exemplu

maximului de oscilație sau minimului

sau zerourilor să trecem la un

de plan modelul Andi plane implică

două concepte primul concept este

legat de proprietățile mediului

Deci mediul este elastic asta înseamnă

că forțele si propaganda blând

oscilatorii sunt de tip elastic

adică altfel spus o și laturi sunt

armonici mediul de asemenea este

net disipativ nu avem pierderi

de energie amplitudinea oscilațiilor

rămânând constantă în timp și omogen

care implică ceea ce am discutat

mai cel de al doilea concepte de

baza al în de plane se referă la

geometria unde e Plein și este

următorul bineînțeles acela când

ai este plan acest această geometrie

plană a undei apare după un timp

îndelungat de propagare Deci când

timpul acest timp de propagare

tinde către infinit de un timp

îndelungat curbura suprafeței devine

neglijabilă curbura fiind definită

ca inversul razei în punctul active

și AD unde ad vine plană ca să

explicăm vizuala acest lucru bineînțeles

un De ce se propagă imediat după

producerea ala sus este sferică

după cum am discutat totuși dacă

luăm un segment de cerc sau un

segment de sferă vedem că Pe măsură

ce ne îndepărtăm de sursă acest

segment devine din ce în ce mai

drept Deci considerăm un segment

de aproximativ aceeași lungime

și vedem că aproape de Sus El este

curbat Da curbura lui Pe măsură

ce raza crește scade devenind la

distanțe mari sau la raze mari

devenind un segment drept Deci

când ne aflăm la distanțe mari

de Sus să putem aproxima u bucată

din suprafața de undă destul de

mare când o dreaptă sau în trei

dimensiuni