Mişcarea circulară uniformă: mărimi caracteristice, acceleraţia centripetă.

Mișcarea circulară uniformă

Definiție

Mișcarea circulară uniformă este mișcare pe o traiectorie în formă de cerc cu viteza constantă în mărime.

În mișcarea circulară uniformă vectorul viteză își schimbă în permanență orientarea (direcția și sensul), dar modulul vitezei rămâne constant.

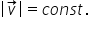
Pe timpul mișcării circulare uniforme, mobilul va parcurge arce de cerc egale în intervale de timp egale.

Parametri mișcării circulare uniforme

Mișcarea circulară uniformă este caracterizată de un centru de rotație și o rază de curbură numită și rază vectoare.

Dacă considerăm centrul de curbură O ca punct de referință, atunci raza vectoare coincide cu vectorul de poziție al mobilului.

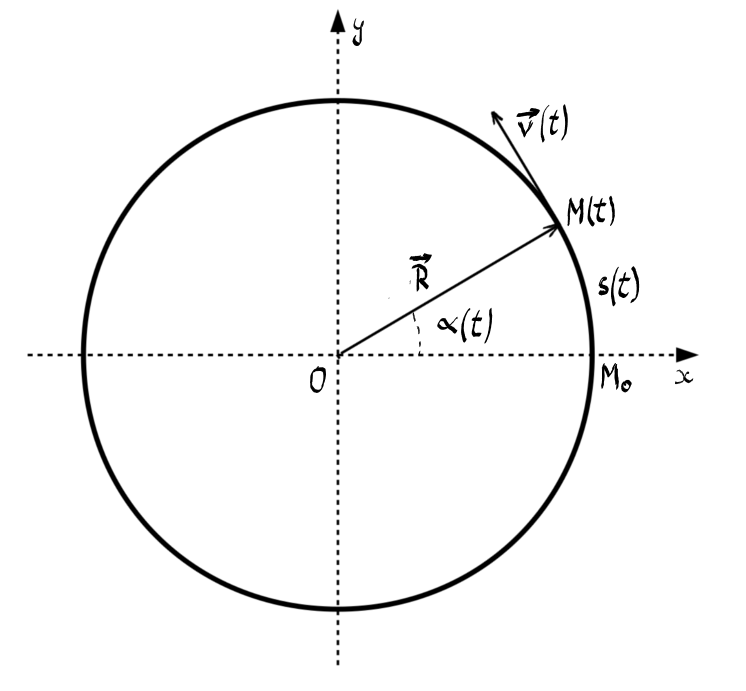
Raza vectoare este constantă în modul fiind egală cu raza cercului, dar are direcția și sensul dependente de timp.

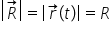
Perioada mișcării reprezintă timpul necesar efectuării unei rotații complete.

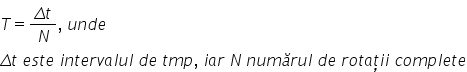
Perioada se măsoară în secunde:

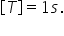
Frecvența este numărul de rotații efectuate în unitatea de timp.

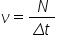
Frecvența se măsoară în:

.

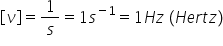Observăm că frecvența este inversa perioadei sau:

.

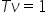Ecuația abscisei curbilinii

Pentru calculul vitezei ținem cont de faptul că o rotație completă este efectuată într-un interval de timp egal cu perioada de rotație:

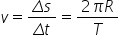
sau dacă înlocuim perioada cu frecvența:

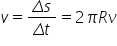
Pornind de la relația vitezei putem deduce o lege de mișcare, numită legea sau ecuația abscisei curbilinii, care descrie distanța parcursă de mobil pe cerc.

Considerând:

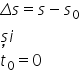
rezultă,

.

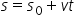Viteza unghiulară și ecuația abscisei unghiulare

Observăm că lungimea unui arc de cerc este proporțională cu raza cercului și cu unghiul la centru determinat de arcul de cerc.

Pentru a putea scrie lungimea arcului de cerc în funcție de unghiul la centru se introduce o unitate de măsură pentru unghiuri numită radian (prescurtat rad).

Un radian reprezintă unghiul la centrul unui cerc ce determină pe cerc un arc de cerc cu lungimea egală cu raza cercului.

Pornind de la această defniție rezultă că:

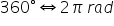
Pentru a determina unghiul în radiani folosim relația:

.

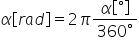Folosind noua unitate de măsură pentru unghiuri putem scrie:

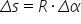
Dacă scriem încă odată relația de definiție a vitezei rezultă:

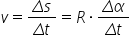
Variația unghiului la centru în unitatea de timp se numește viteză unghiulară:

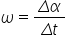
Unitatea de măsură pentru viteza unghiul ară este:

.

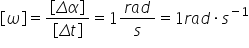Folosind viteza unghiulară deducem legea sau ecuația abscisei unghiulare.

Considerând:

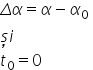
rezultă,

.

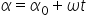Accelerația centripetă

În mișcarea circulară uniformă modulul vitezei este constant în timp dar direcția și sensul vitezei sunt dependente de timp.

Mișcarea circulară uniformă este o mișcare accelerată.

Pentru deducerea accelerației considerăm două poziții ale mobilului pe traiectoria sa circulară:

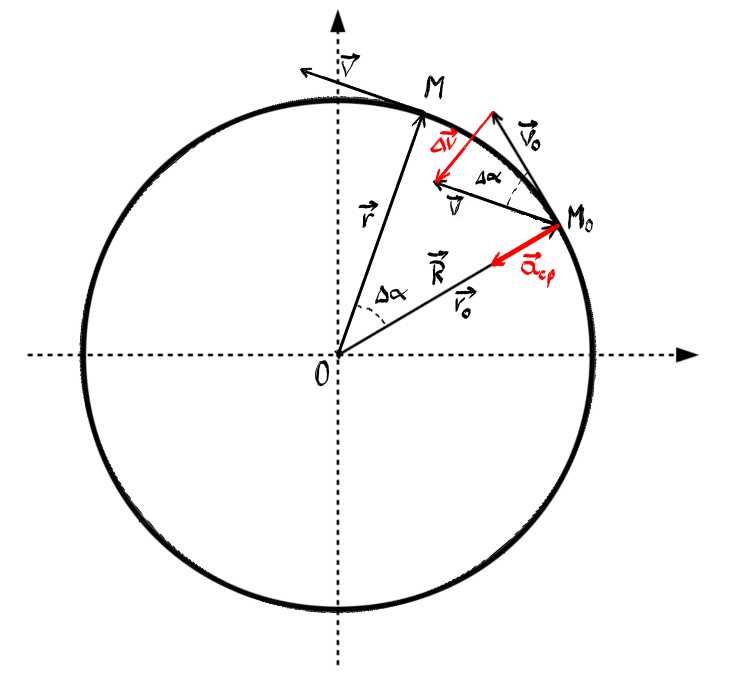
Aceelerația se determină cu relația:

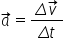
Pentru a calcula variația vitezei, translatăm viteza finală în același punct cu viteza inițială,

Observăm că avem două triunghiuri asemenea, unul determinat de cele două viteze și variașia vitezei și unul determinat de cele două raze vectoare și secanta cercului.

Din asemănare putem scrie:

.

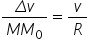Deoarece vrem să determinăm accelerația instantanee reducem intervalul de timp la unul infinetizimal.

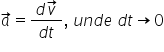
În această situație si secanta devine foarte mică și putem considera că este egală cu lungimea arcului de cerc.

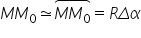
Introducem relația în relația de asemănare și calculăm variația vitezei:

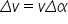
pe care o introducem în relația de calcul a accelerației și rezultă:

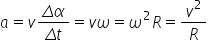
Vectorul viteza este perpendicular pe raza vectoare, iar variația infinitezimală a vitezei este perpendiculară pe viteză, deci are aceeași direcție cu raza vectoare dar sens opus. Cum accelerația are direcția și sensul vectorului variație a vitezei putem spune că și accelerația are direcția razei vectoare dar sens opus acesteia. Putem scrie aceelearația, pe care o numim accelerație centripetă:

.
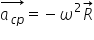