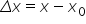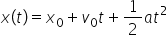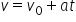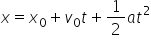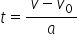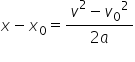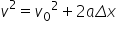Mișcarea rectilinie uniform variată
Mișcarea rectilinie uniform variată este mișcarea în linie dreaptă cu accelerație constantă.
Mișcarea rectilinie uniform variată a unui mobil poate fi reprezentată schematic ca mai jos.
Legea vitezei
Dacă cunoaștem proprietățile mișcării în două stări, inițială notată cu A și finală notată cu B, din definiția accelerației rezultă:
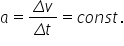
Exprimând variația vitezei și intervalul de timp rezultă:
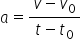
și considerând că:
,
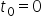rezultă:
.
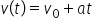Relația obținută se numește legea vitezei.
Dacă acelerația este pozitivă atunci viteza crește odată cu timpul, iar dacă accelerația este negativă atunci viteza scade odată cu timpul.
Din punct de vedere matematic, legea vitezei este o funcție de gradul I care descrie dependența vitezei de timp.
Dacă reprezentăm grafic legea vitezei în coordonate tOv rezultă un grafic de forma unei drepte:
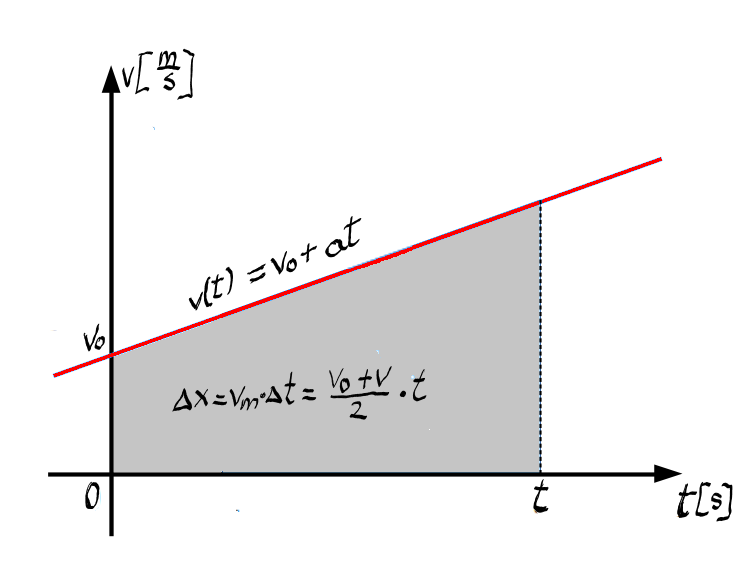
Legea de mișcare
Pentru deducerea legii de mișcare a mișcării rectilinii uniform variate ne folosim de relația de definiție a vitezei medii:
.
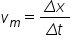De asemenea datorită faptului că viteza variază liniar cu timpul atunci, putem determina viteza medie cunoscând două valori ale vitezei momentane:
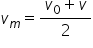
Considerând că:
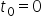
și folosind cele două relații enunțate mai sus rezultă că:
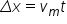
adică,
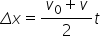
Dacă analizăm din punct de vedere geometric graficul vitezei în funcție de timp, constatăm că distanța parcursă între momentul inițial și cel final este reprezentată de aria cuprinsă între graficul vitezei și axa timpului.
Putem generaliza această afirmație pentru orice tip de mișcare.
Pentru obținerea legii de mișcare înlocuim viteza la momentul t în relația de mai sus și rezultă:
,
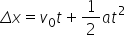și cum,
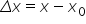
rezultă legea de mișcare:
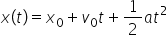
Legea de mișcare este din punct de vedere matematic o funcție de gradul II care descrie poziția mobilului în funcție de timp.
Legea lui Galilei
Considerăm legea vitezei și legea de mișcare:
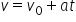
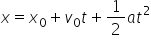
Deducem timpul din legea vitezei:
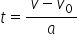
și îl înlocuim în legea de mișcare. Rezultă:
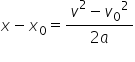
sau:
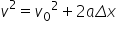
Relația poartă numele de legea lui Galilei, ea fiind dedusă pentru prima dată de Galileo Galilei.
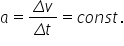
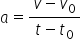
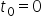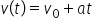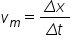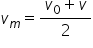
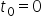
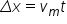
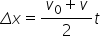
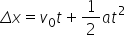