Noţiuni şi mărimi cinematice. Ecuaţia de mişcare. Definiţia şi proprietăţile vectorilor.

Mărimi fizice

Mărimea fizică este o mărime ce caracterizează o proprietate sau o stare a unui corp sau sistem fizic. Mărimea fizică descrie cantitativ (numeric) proprietatea sau starea prin raportare la o unitate de măsură a mărimii fizice ce este convenită în prealabil.

Mărimile fizice sunt de două feluri:

Mărimi fizice scalare

Pentru exprimarea unei mărimi fizice scalare este suficient un număr care arată raportul între mărime si unitatea de măsură a mărimii fizice. De exemplu masa unui corp exprimă un anumit număr de kg, temperatura un număr de ºC, etc.

Mărimi fizice vectoriale

O mărime fizică vectorială are trei proprietăți:

- mărime sau modul sau magnitudine - este numărul de unități de măsură;

- direcție - dreapta în lungul căreia este orientată mărimea vectorială;

- sens - orientarea mărimii vectoriale.

De exemplu: un avion zboară de la est la vest 500 de km. Pentru a descrie deplasarea avionului nu este suficientă mărimea - 500 km, mai trebuie specificată directia - est-vest și sensul spre vest.

Notația științifică a mărimilor fizice

Pentru exprimarea unor mărimi fizice foarte mari sau foarte mici se folosește notația exponențială sau științifică. Ea are forma:

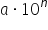
unde a se numește mantisă și n se numește exponent.

Mantisa este de regulă un număr cuprins între 1 și 10. Uneori, în special când comparăm mărimi fizice, se acceptă și numere subunitare sau mai mari de 10. Mantisa conține un set de cifre semnificative. Exponentul ne descrie ordinul de mărime al mărimii fizice exprimate.

Exemplu: Distanța de la Pământ la Soare este de 149.600.000 km. ea poate fi scrisă:

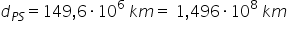
Diametrul atomului de hidrogen este de aproximativ 0,00000000011 m sau a zecea miliarda parte dintr-un metru. Diametrul poate fi scris:

.

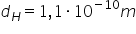Domeniile mecanicii clasice

Mecanica clasică se împarte în trei mari părți sau domenii.

1. Cinematica - se ocupă cu studiul mișcării fără a analiza cauzele acesteia mulțumindu-se să descrie mișcarea.
2. Dinamica - se ocupă cu studiul cauzelor mișcării corpurilor.
3. Statica - se ocupă cu studiul echilibrului corpurilor în interacțiune cu alte corpuri.

Punct material. Mobil

În foarte multe situații dimensiunea corpurilor studiate este foarte mică (neglijabilă) în raport cu distanțele parcurse sau cu distanțele până la corpurile înconjurătoare sau pur și simplu în gradul de aproximare în care lucrăm nu ne interesează forma corpului studiat. În acestă situație se poate aproxima corpul cu un punct numit punct material. Punctul material este caracterizat doar de masa sa.

Dacă studiem doar cinematica punctului material masa lui nu va fi relevantă și atunci punctul material se va numi mobil.

Mișcare și repaus

Pentru determinarea stării de mișcare a unui corp este nevoie de un al doilea corp, numit corp de referință sau reper sau observator.

Dacă poziția corpului studiat se modifică în raport cu reperul atunci corpul se află în mișcare. Dacă poziția corpului studiat nu se modifică în raport cu reperul atunci corpul este în repaus.

Putem constata că starea de mișcare sau de repaus este realtivă, ea depinzănd de starea reperrului. Spre exemplu un călător aflat într-un autobuz care se mișcă este în mișcare față de pământ dar în repaus față de autobuz.

Pentru a studia mișcarea unui corp avem nevoie pe lângă corpul de referință de un instrument de măsurat distanțele - riglă și de unul de măsurat timpul - ceas.

Corpul de referință, rigla și ceasul formează sistemul de referință.

De fiecare dată când studiem mișcarea unui corp alegem  mai întâi sistemul de referință în care vom studia mișcarea.

Mulțimea punctelor prin care trece un corp în mișcarea sa se numește traiectorie. În funcție de traiectoria sa mișcarea unui corp poate fi:

1. Mișcare rectilinie - mișcare în linie dreaptă.
2. Mișcare circulară - mișcare în formă de arc de cerc sau de cerc.
3. Mișcare curbilinie - mișcare pe o traiectorie curbă.

Traiectoria depinde de sistemul de referință ales pentru studierea mișcării.

Ecuația de mișcare sau legea de mișcare

Cea mai simplă mișcare este cea rectilinie. Pentru studiul ei se alege un sistem de referință unidimensional. cu o axă de coordonate ce coincide cu direcția de mișcare.

Din studierea mișcării rezultă un set de date în care fiecărui moment de timp îi corespunde o singură poziție în spațiu, o singură coordonată pe axa Ox.

Relația dintre momentul de timp t și poziție

,

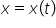se numește lege sau ecuație de mișcare.

Din punct de vedere matematic legea de mișcare este o funcție. Sistemul de referință ales și legea de mișcare descriu complet mișcarea mobilului.

Pentru mișcări mai complexe, mișcare circulară sau curbilinie, este nevoie de alegerea unui sistem de refeință unde determinarea poziției spațiale a mobilului să necesite două sau trei coordonate spațiale. în acest caz se alege convenabil un sistem de coordonate xOy sau xOyz. Mișcarea ce poate fi descrisă cu două coordonate spațiale se numește mișcare bidimensională sau mișcare în plan, iar miscarea descrisă de trei coordonate spațiale se numește mișcare tridimensională sau mișcare în spațiu.

Pentru descrierea mișcării, pe lângă sistemul de coordonate xOyz, numit și sistem de coordonate cartezieine, se mai pot alege și alte sisteme de coordonate.

Exemplu: Sistemul GPS folosește pentru determinarea coordonatelor unui punct de pe suprafața Pământului trei coordonate: latitudine, longitudine și altitudine.

Pentru mișcarea în plan vom obține câte o lege de mișcare pentru fiecare axă de coordonate:

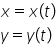
Pentru mișcarea în spațiu vom obține:

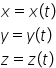
Mișcarea se poate descrie și cu ajutorul vectorului de poziție. Vectorul de poziție este vectorul ce leagă punctul de referință de poziția mobilului la un moment dat.

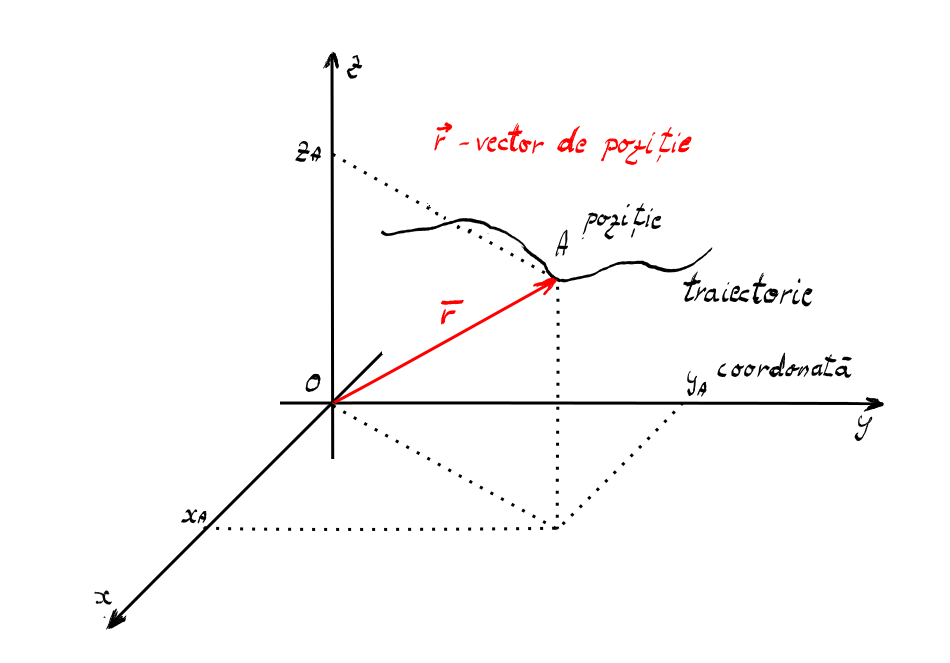
Mișcarea mobilului poate fi descrisă printr-o lege de mișcare vectorială:

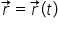
Între descrierea vectorială a mișcării și descrierea cu ajutorul coordonatelor cartezieine este o relație de echivalentă.

Mărimea vectorului de poziție este:

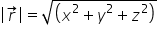
iar orientarea vectorului de poziție poate fi determinată de două unghiuri calculate tot cu ajutorul coordonatelor.

Dacă se atașează fiecărei axe un vector unitar, numit versor, atunci legea de mișcare vectorială se poate scrie: