Operaţii cu vectori. Viteza şi acceleraţia.

Adunarea și scăderea vectorilor

Vectorii se pot aduna după metoda paralelogramului.

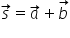
Se așează cei doi vectori astfel încât să aibă originea în același punct. Se construiește un paralegram ducând paralele la cei doi vectori prin vârfurile lor. Vectorul sumă va fi diagonala paralelogramului cu originea în originea comună a celor doi vectori.

De asemenea vectorii se pot aduna folosind metoda patrulaterului.

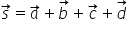
Se așează vectorii succesiv unul cu originea în vârful celuilalt. Vectorul sumă va fi vectorul cu originea în originea primului vector și vârful în vârful ultimului vector.

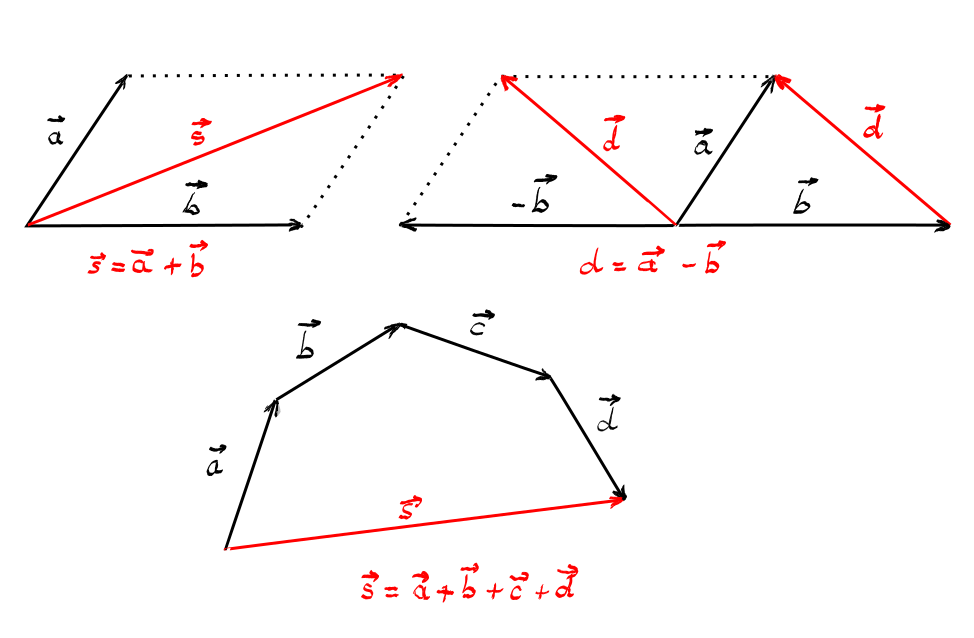
Scăderea a doi vectori înseamnă adunarea descăzutului cu opusul scăzătorului.

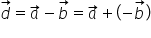
Folosind metoda paralelogramului se demonstrează că diferența a doi vectori este vectorul de unește vârful scăzătorului cu vărful descăzutului.

Dacă vectorii sunt ortogonali (perpendiculari unul pe altul), paraleogramul devine dreptunghi. La calculul mărimii sumei și diferenței se poate folosi teorema lui Pitagora. Vectorii sumă și diferență vor avea aceeași mărime sau modul, dar vor avea orientări diferite.

Dacă vectorii sunt coliniari, atât suma cât și diferența se vor calcula algebric, ținându-se cont de sensul vectorilor.

Viteza

Viteza reprezintă distanța parcursă în unitatea de timp. Viteza este o mărime vectorială.

Viteza în mișcarea rectilinie

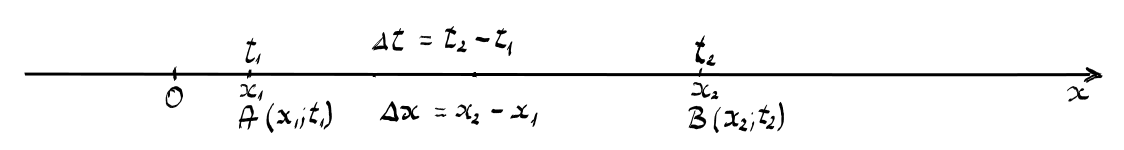
Dacă avem un mobil ce efectuează o mișcare rectilinie și determinăm două poziții, A și B, ale mobilului, atunci putem calcula distanța parcursă de mobil:

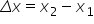
și intervalul de timp necesar parcurgerii acestei distanțe:

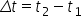
În această situație, viteza medie pe porțiunea AB, va fi:

.

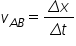Unitatea de măsură a vitezei in sistemul internațional de măsuri și unități este:

.

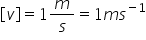Dacă vrem să determinăm viteza momentană sau viteza la momentul t, atunci trebuie să alegem un interval de timp infinitezimal, care tinde la zero. În această situație și distanța parcursă de mobil este și ea infinitezimală, adică foarte mică, dar viteza este o mărime diferită de zero dacă distanța parcursă este diferită de zero.

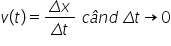
sau

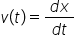
Viteza în mișcarea curbilinie

Dacă avem o mișcare curbilinie, atunci vom descrie pozițiile mobilului cu ajutorul vectorului de poziție.

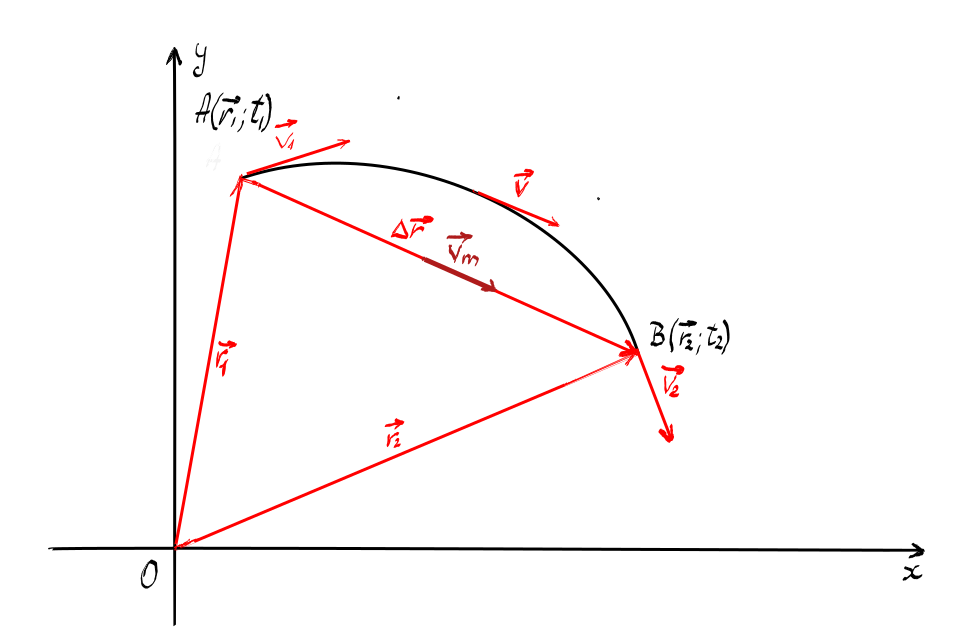
Dacă determinăm două poziții,

,

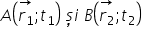de pe traiectoria mobilului, atunci putem determina vectorul deplasare și intervalul de timp:

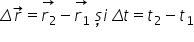
Viteza medie este mărimea vectorială exprimată prin relația:

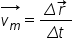
Viteza medie are direcția și sensul vectorului deplasare.

Pentru determinarea vitezei la un moment dat alegem un interval de timp infinitezimal. În acest caz cele două puncte de pe traiectorie sunt foarte apropiate, iar vectorul deplasare tinde să devină din secantă la traiectorie, tangentă al traiectorie. Viteza la momentul t este:

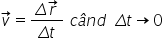
sau

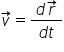
Putem afirma că viteza la momentul t sau viteza momentană este tangentă la traiectorie.

Accelerația

Accelerația este mărimea vectorială egală cu variația vitezei în unitatea de timp.

Cunoscând vitezele momentane în două pozițiiA și B,  de pe traiectoria unui mobil, putem determina vairația vitezei și intervalul de timp necesar parcurgerii distanței de al A la B:

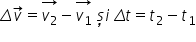
Accelerația medie între cele două poziții A și B este:

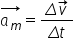
Unitatea de măsură a accelerației este:

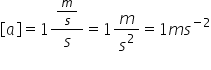
În cazul mișcării rectilinii, dacă viteza crește accelerația este pozitivă, iar dacă viteza scade accelerația este negativă.