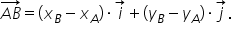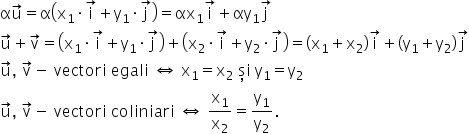Despre Lecții-Virtuale.ro
Lecții-Virtuale este o platformă educațională care oferă suport în vederea pregătirii pentru Evaluare Națională și Bacalaureat la Matematică, Fizică și Chimie. Lecțiile noastre sunt alcătuite din filme și exerciții și probleme cu tot cu rezolvări. Platforma noastră este o soluție ideală pentru școala online. Pentru facilitarea activității profesorilor în cadrul ecosistemului GSuite de la Google am implementat butonul Google Classroom. Scopul nostru este să ne concentrăm pe prezentarea noțiunilor și fenomenelor într-o manieră care să stimuleze înțelegerea și nu memorarea mecanică. Ne propunem să facilităm accesul la conținut educațional de calitate mai ales elevilor cu venituri mai modeste care nu își pemit meditații particulare. Sperăm să vă simțiti bine alături de noi și să invățați lucruri folositoare. Hai România!

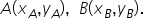
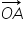 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: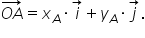
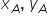 se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului
se numesc coordonatele carteziene ale punctului A sau coordonatele vectorului 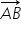 se descompune după direcțiile date de cei doi versori astfel:
se descompune după direcțiile date de cei doi versori astfel: