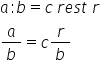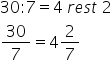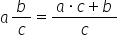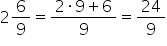Scoaterea întregilor din fracție. Introducerea întregilor în fracție

să învățăm acum cum să scoatem

întregii din fracție și cum să

introducem întregii în fracție

și vom Începe prin a scoate întregii

din această fracție 25 supra 4

și Haideți să Reprezentăm fracția

dată cu ajutorul unor desene cum

o putem reprezenta Păi numitorul

este 4 asta înseamnă că întregul

trebuie să fie împărțit în câte

părți în patru părți egale bun

însă mai observăm și că fracția

este supraunitară este mai mare

decât unul si ne spune acest lucru

că vom avea mai mult de un întreg

și atunci Haideți Să considerăm

că întregul este acesta Deci avem

un pătrat care este împărțit în

patru părți egale și le vom alege

pe toate patru cifra ție vom obține

Păi avem numitorul este 4 am patru

părți Deci fracția 4 supra 4 Păi

mai avem până la 25 pe 4 Deci mai

adăugăm încă un întreg bun și acum

vom alege tot patru tot cele patru

părți Deci alegem tot întregul

și avem din nou 4 supra 4 aceste

desene împreună ce fracție reprezintă

pe Avem doi întregi egali fiecare

este împărțit în patru părți egale

Care este numitorul Păi numitorul

este 4 câte părți am ales Păi avem

una două trei patru cinci șase

șapte opt Deci numărătorul este

8 bun dar până la 25 pe 4 mai avem

Deci vom mai adăuga încă un întreg

și tot așa vom alege cele patru

părți Deci avem din nou fracția

4 pe 4 cât obținem aici Păi am

ales patru cu patru cu încă patru

Deci avem fracția 12 pe 4 mai avem

mai trecem încă un întreg și tot

așa alegem cele patru părți Deci

din nou patru pe patru am ajuns

la a ta avem patru părți a câte

4 întregi Deci 16 numărătorul 16

Mai avem până la 25 mai alege încă

patru deci din nou notăm fracția

4 supra 4 am ajuns la 20 supra

4 mai avem nevoie până la 25 din

nou hașură Maicii cât am obținut

din nou 4 pe 4 Păi în acest moment

Toate aceste fracții Cât reprezintă

pe observăm că patru patru părți

a câte 5 întregi sau 6 întregi

pardon 1 2 3 4 5 6 de 6 întregi

patru părți fiecare înseamnă că

avem 24 supra 4 și mai avem nevoie

de încă o parte până la 25 pe patru

deci mai trece îmi pun întreg și

cât vom hașura din acest întreg

pe o singură parte Deci avem aici

fracția 1 supra 4 Deci numitorul

este 4 Haide să șterg numitorul

cum am spus este 4 se observă Da

și câte părți am ales Păi avem

24 Toate aceste părți una Deci

25 pe 4 Câți întregi avem pe avem

1 2 3 4 5 6 întregi de 6 întregi

și o pătrime asta înseamnă că fracția

25 supra 4 o putem scrie șase întregi

și o pătrime acum ce avem aici

este o notație care ne arată Câți

întregi avem făcând acest lucru

spunem că am scos întregii din

această fracție Cum facem acum

mai simplu ca să nu fie nevoie

să facem aceste desene mereu Păi

de fapt ce am făcut am văzut de

câte ori intră numărul 4 în 25

pentru că noi am obținut acești

întregi 4 supra 4 și apoi am pus

să vedem de câte ori în numărătorul

4 Se cuprinde în 25 de fapt am

făcut împărțirea cu rest a lui

25 la 4 iar dacă facem împărțirea

cu rest 25 împărțit la 4 vom obține

6 x 4 24 și restul 1 restul Ce

rezultă conform teoremei împărțirii

cu rest deîmpărțitul adică 25 se

scrie ca produsul dintre împărțitor

și cât Deci patru ori 6 adunat

cu restul Care este unul bun asta

înseamnă că 25 supra patru fracții

au putem scrie astfel copiem numitorul

4 iar la numărător ce scrie patru

ori 6 Care înseamnă 24 plus unu

adică 25 Am aplicat aici teorema

împărțirii cu rest acum Poate costă

vi se pară complicat faptul că

avem așa de multe operații aici

la numărător însă eu cred că e

destul de simple explicația care

urmează și eu puteți înțelege și

anume aici avem operație de înmulțire

deci de fapt acest calcul este

un termen al acestei sume vom separa

această fracție în două fracții

în nostru sumă de două fracții

putem să facem acest lucru și Avem

așa patru ori 6 supra 4-a prima

fracție adunat cu 1 pe 4 este același

lucru cu ce am notat aici ce vom

obține pe linia de fracție operație

de împărțire 4 înmulțit cu 6 împărțit

la 4 adică 24 împărțit la 4 ne

dă 6 Deci avem șase plus unu pe

patru și atât că de fapt am obținut

că 25 pe 4 reprezintă de fapt 6

întregi adunat cu o pătrime exact

ce am făcut și aici și se folosește

această notație Deci voi scrie

pe egal înot de la notație 6 și

1 pe 4 și 6 întregi și 1 pe 4 adică

nu se mai trece acest samplus în

să reținem că aceasta este o notație

care reprezintă de fapt această

operație 6 plus 1 pe 4 care ne

dă 25 supra 4 haide să mai facem

acum încă un exemplu ca să ne învățăm

cu acest mod de calcul 30 supra

7 Cum scoatem întregii din această

fracție împărțim mai întâi numărătorul

la numitor Deci vom avea 30 împărțit

la 7 obținem patru ori 72810 restul

este 2 4 rest 2 ce rezulta conform

teoremei împărțirii cu rest că

deîmpărțitul adică 30 se scrie

ca produsul dintre împărțitor și

cât de 7 ori 4 adunat cu restul

Care este doi Deci venim aici notăm

copiem numitorul Care este 7 iar

la numărător vom avea șapte ori

patru adică 28 plus doi 30 separăm

acuma această fracție ca mai sus

pentru o sumă de două fracții prima

fracție 7 ori 4 supra 7 adunat

cu cine a rămas 2 pe 7 și folosind

notația pe care am învățat tot

pentru că iată cât vom avea aici

Păi 28 împărțit la șapte ne dă

patru Haide să scriem Mai detaliat

4 adunat cu 2 pe 7 Deci cum avea

patru întregi și doi pe șapte acum

să știți că putem să scriem direct

Nu e neapărat nevoie să facem tot

Acest calcul detaliate și putem

să reținem următoarea regulă de

calcul și anume facem împărțirea

numărătorului la numitor obținem

aici câtul și restul da câtul reprezintă

numărul de întregi iar 4 întregi

iar restul va fi noul numărător

doi ne apare aici la numărător

iar numitorul 7 îl copie de ceai

de să facem un exemplu în care

să scriem direct 24 pe 9 facem

împărțirea 24 împărțit la 9 avem

doi ori 9 18 și obținem aici 6

deci 2 rest 6 și vom avea câtul

câtul este acesta este 2 iar restul

este 6 deci venim și notăm câtul

reprezintă numărul de întregi Deci

2 întregi copiem numitorul Care

este 9 iar restul reprezintă noul

numărător de 6:00 nu trecem aici

Dacă făceam calculul detaliat cum

am făcut în acest exemplu obțineam

același lucru 2 întregi și 6 pe

9 acum Haideți să simu să spunem

așa operația inversă adică vom

introduce acum întregii în fracție

vom porni de la acest exemplu să

vedem cum facem să ajungem la 24

supra 9 Prin urmare avem această

fracție 2 întregi și 6 pe 9 și

vrem să introducem întregii în

fracție pe ce avem aici ce am spus

că este o notație deci a reprezintă

de fapt această operație 2 întregi

adunat cu 6 pe 9 Deci 2 plus 6

supra 9 și acum Păi 2 întregii

putem scrie un întreg plus 1 întreg

adunat cu 6 pe 9 Dar un întreg

îl putem scrie astfel 9 pe 9 pentru

copt serbăm că aici întregul împărțit

în nouă părți egale adunat mai

departe cu 9 supra 9 și acum facem

acest calcul pe unii dintre voi

deja știi să Adunați fracții care

au același numitor se copiază numitorul

și adunăm numărătorii dacă nu știm

putem să gândim în felul următor

folosind un tot de desene și anume

Haideți să scrie mai jos 9 supra

9 îl putem reprezenta prin acest

desen și avem aici trebuie să împărțim

în nouă părți egale Una două trei

patru cinci șase șapte opt nouă

Considerăm că sunt părți egale

Deci hașu rând tot Acest întreg

avem fracția 9 pe 9 vom face la

fel pentru că mai avem nevoie de

încă un întreg Deci Haide să copiem

și avem următoarea fracție și ne

mai trebuie desenul pentru fracția

6 pe 9 Haideți să împărțim tot

în nouă părți și vom Alege șase

Deci una două trei patru cinci

șase avem șase pe 9 care e numitorul

Păi fiecare întreg a fost împărțit

în nouă părți egale Deci vom avea

numitorul este nouă și ce obținem

la numărător Păi el câte părți

am ales avem nouă părți Mai avem

încă nouă părți pe care le alegem

adunat cu 6 părți adică exact ceva

spus când adunăm fracții cu același

numitor și vom obține 9 cu 918

cu 6 24 supra 9 adică exact ce

aveam aici Multe evident că putem

să facem acest calcul și direct

fără să fie nevoie să facem așa

detaliat și pentru aceasta Haideți

să luăm exemplul anterior pe care

îl am făcut și anume care era aveam

aici și 4 întregi și 2 supra 7

4 întregi și 2 supra șapte Cum

introducem acum întregii în fracție

și aici putem să aplicăm următoarea

regulă Deci în loc să facem așa

detaliat vom muta avem numitorul

îl copiem 7 iar la numărător vom

obține Înmulțind întregul cu numitorul

Deci patru ori 7 adunat cu doi

și vom obține aici 7 4 x 7 28 plus

doi Deci ne dă 30 supra 7 adică

exact ce aveam mai sus aceasta

este varianta scurtă Deci folosind

de fapt această regulă figura această

regulă se datorează faptului că

întru asemenea sumă aduce la același

aducem fractiile la același numitor

însă acest lucru îl vom învăța

ceva mai târziu un alt exemplu

Haide să calculăm acum un întreg

și 3 supra 8 să introducem întregii

în fracție copiem numitorul 8 la

numărător înmulțim întregul cu

numitorul Deci avem unul ori opt

adunat cu 3 și cât avem 8 plus

3 supra 8 Deci am obținut 11 supra

8 alt exemplu Să considerăm acum

că avem 0 întregi și 5 pe 6 să

vedem ce vom obține Păi folosim

regula pe care am învățat și avem

numitorul copie la numărător înmulțim

întregul cu numitorul Deci 0 ori

6 plus și trecem aici pe 5 Păi

06 ne dă 0 plus 5 adică 5 pe 6

Păi nu era nou masa obținem 5 supra

6 de ce Pentru că 0 întregi și

5 pe 6 iar cele lucru cu 0 adunat

cu 5 supra 6 aceasta este doar

o notație Deci adunând zero Orice

număr de de numărul respectiv adică

5 supra 6 exact ce am obținut și

aici ca să reținem putem să notăm

și această regulă Haideți să se

vadă ce am mutat aici atunci când

scoate întregii din fracție cum

a fost în acest în această situație

Deci dacă avem a supra b o fracție

facem a împărțit la b și vom obține

un cât și un rest notat R deîmpărțitul

a se scrie ca fiind produsul dintre

împărțitor și cât Deci avem b ori

c plus R venim și notăm copiem

numitorul iar în loc de Avon scrie

B orice b ori c plus R și ce vom

obține Putem să scriem direct fără

să mai facem acest calcul câtul

reprezintă întregul Deci avem ce

întregi copiem numitorul Care este

b iar restul reprezintă noul numărător

adică exact ce avem aici invers

dacă vrem să introducem întregii

în fracție dacă mi se dă această

fracție ce întregi și R supra b

folosim aceleași litere si vom

avea Păi cum am spus este o notație

și vom obține conform calcului

pe care îl am învățat Iată aici

la acest exemplu scrie numitorul

b iar la numărător înmulțim întregul

cu numitorul Deci avem si ori b

și a adunăm restul adică el Păi

nu e același lucru ca mai sus Ba

da Ia să avem aici si ori b adică

b ori c plus R plus aer totul supra

exact ce avem aici deci a introduce

întregii în fracție e să spunem

așa operația inversă scoate întregii

lor din fracție și ne dă ca mai

sus a pe b noi neapărat nevoie

să rețineți aceste formule să le

spunem așa acestor reguli de calcul

mai bine zis și făcând suficient

de multe exerciții în care să fie

nevoie să scoateți întregii dintre

o fracție sau să introduceți întregii

în fracție atunci deja o să stăpâniți

foarte bine aceste reguli de calcul