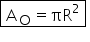Aria cercului (discului) și aria sectorului de cerc

în prima imagine avem un hexagon

regulat înscris în cerc iar în

a doua imagine avem un octogon

putem observa că atunci când numărul

de laturi ale Poligonului înscris

în cerc crește lungimea acestora

scade iar laturile Poligonului

Se apropie tot mai mult de lungimea

cercului în cazul în care avem

în Poligonul cu un număr foarte

mare de la acesta va aproxima aria

discului Să presupunem că avem

în ultima imagine un poligon cu

n laturi în care am dus apotema

am notat vârfurile Poligonului

cu a 1 a 2-a 3 și așa mai departe

având în vedere că acest poligon

are n laturi el poate fi împărțit

în triunghiuri iar aria acestui

poligon va fi suma ariilor acelor

triunghiuri astfel aria Poligonului

ei finală cu n ori aria triunghiului

A1 o A2 egal cu n ori aria triunghiului

este baza ori înălțimea supra 2

baza este a1 a2 iar înălțimea este

apotema Poligonului supra 2 egal

Putem să scriem n ori a 1-a 2 ori

apotema supra 2 Dar n ori a 1-a

2 formează perimetrul Poligonului

egal cu perimetrul ori apotema

supra 2 Așadar aria acestui poligon

cu n laturi este egală cu perimetrul

ori apotema supra 2 Dacă n este

foarte mare atunci aria Poligonului

va fi egală cu aria discului să

calculăm Așadar aria discului perimetrul

Poligonului va coincide cu lungimea

cercului iar dacă avem un număr

foarte mare de laturi apotema Poligonului

devine raza cercului supra 2 lungimea

cercului este 2 pi r ori Air supra

2 se simplifică 2 și obținem pi

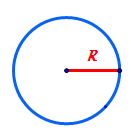
R patrat și aceasta va fi formula

de calcul pentru aria unui disc

ori r pătrat unde R este raza cercului

de exemplu dacă avem un disc cu

raza egală cu 8 cm aria sa va fie

egală cu pi ori 8 la a doua și

egal cu 64 Pi cm pătrați în continuare

trecem la aria unui sector de cerc

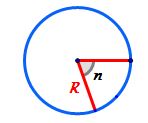
se numește sector de cerc o porțiune

din interiorul unui cerc cuprinsă

între două raze ale sale un sector

de cerc va corespunde unui arc

de cerc având măsura egală cu n

grade pentru a calcula formula

ariei unui sector de cerc pornim

de la regula de trei simpla dacă

un cerc întreg are 360 de grade

iar aria discului este pi R patrat

atunci un sector care are măsura

unghiului la centru egală cu n

grade va avea aria egală cu x aria

sectorului este direct proporțională

cu numărul n adică cu măsura arcului

Pentru că atunci când măsura arcului

AB crește la crește și suprafața

sectorului de cerc și atunci folosim

regula de trei simpla pentru mărimi

direct proporționale X va fi egal

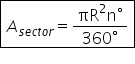
cu n p r pătrat supra 360 de grade

aceasta va fi formula de calcul

pentru aria unui sector circular

fier pătrat n supra 360 unde n

este măsura arcului AB