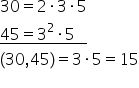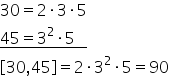Cel mai mare divizor comun (c.m.m.d.c.) şi cel mai mic multiplu comun (c.m.m.m.c.)
Tag-uri
Partajeaza in Google Classroom

Transcript
cel mai mare divizor comun și cel
mai mic multiplu comun două sau
mai multe numere pot avea mai mulți
divizori comun de exemplu se scrie
mulțimea divizorilor numărului
10 divizorii numărului 10 sunt
1 2 5 și 10 să scriem acum mulțimea
divizorilor numărului 20 aceasta
este formată din numerele 1 doi
patru 5 10:20 să vedem Ce elemente
comune au cele două mulțimi mulțimea
divizorilor lui 10 intersectată
cu mulțimea divizorilor lui 20
este egal cu mulțimea formată din
numerele 1 2 5:10 Aceștia sunt
divizorii comuni ai numerelor 10
și 20 și Dintre aceștia cel mai
mare este 10 cel mai mare divizor
comun a doua sau mai multe numere
naturale este cel mai mare număr
natural care divide numerele date
cel mai mare divizor comun al numerelor
a și b se notează cu paranteză
rotundă a virgulă b două numere
naturale a și b se numesc prime
între ele dacă cel mai mare divizor
comun dintre a și b este 1 să vedem
algoritmul de calcul pentru cel
mai mare divizor comun mai întâi
se descompun numerele în factori
primi apoi se înmulțesc toți factorii
primi comuni Luați o singură dată
cu exponentul cel mai mic O să
vedem imediat câteva exemple cel
mai mic multiplu comun a două sau
mai multe numere naturale este
cel mai mic număr natural diferit
de 0 care este divizibil cu numerele
date cel mai mic multiplu comun
al numerelor a și b se notează
cu paranteză dreaptă a virgulă
b algoritmul de calcul pentru cel
mai mic multiplu comun presupune
următorii pași se descompun mai
întâi numerele în factori primi
apoi se înmulțesc toți factorii
primi comuni și ne comuni Luați
o singură dată cu exponentul cel
mai mare Ce facem acum în exercițiul
pentru a înțelege mai bine acest
algoritm Aflați cel mai mare divizor
comun și cel mai mic multiplu comun
al numerelor 30 și 45 32 16:40
42 și 54 63 105 și 140 vom începe
cu punctul a mai întâi vom Descompune
numerele 30 și 45 în factori primi
30 este divizibil cu 2 deoarece
ultima sarcină este 0 30 împărțit
la 2 este 15 15 este divizibil
cu 3 de o are c suma cifrelor sale
este 6 și 6 se împarte exact la
3 15 împărțit la 3 este 5 iar cinci
este divizibil cu 5 și rezultatul
împărțirii va fi unu vom scrie
că 30 și este egal u2 ori 3 ori
5 Deci am descompus numărul 30
în factori primi trebuie acum Să
descompunem și numărul 45 în factori
primi 45 nu este divizibil cu 2
Doarece ultima sa cifră nu este
pară verificăm divizibilitatea
cu 3 deoarece suma cifrelor sale
este nouă înseamnă că numărul va
fi divizibil cu 3 Așadar vom scrie
în partea dreaptă 345 împărțit
la 3 este 15 15 din nou este divizibil
cu 3 15 împărțit la 3 este 5 5
e divizibil cu 5 iar 5 împărțit
la 5 este 1 45 este egal cu 3 la
puterea a doua deoarece numărul
3 apare de două ori în descompunere
ori 5 astfel am descompus și numărul
45 în factori primi să vedem acum
Cel mai mare divizor comun al numerelor
30 și 45 ne uităm la factorii care
apar în descompunere și mama înmulții
doar factorii comuni la puterea
cea mai mică factorii comuni sunt
3:05 deoarece factorul 2 nu apare
în descompunerea 45 Deci acest
anul vom lua în considerare vom
Ține cont doar de factorii 3 și
5 la puterea cea mai mică adică
3 la puterea întâia ori 5 la puterea
întâia 3 ori 5 egal cu 15 cel mai
mare divizor comun al numerelor
30 și 45 este 15 să vedem acum
Cel mai mic multiplu comun al numerelor
30 și 45 pentru a afla cel mai
mic multiplu comun vom înmulțiri
atât factorii comuni cât și ne
comuni Luați o singură dată la
puterea cea mai mare adică 2 ori
3 la puterea a doua zi se ia numărul
3 cu exponentul cel mai mare ori
5 egal cu 2 ori 9 ori 5 Care este
egal cu 90 cel mai mic multiplu
comun al numerelor 30 și 45 este
90 descompune pe rând numerele
32 16:40 începem cu 32 32 este
divizibil cu 2 rezultatul împărțirii
va fi 16 16 este de asemenea divizibil
cu 2 16 împărțit la 2 este 8 8
se împarte la 2 ce obținem 4 4
se împarte la 2 obținem 2 iar 2
împărțit la 2 este 1 Așadar 32
este egal cu 2 la puterea a cincea
deoarece factorul 2 apare de cinci
ori în această descompunere Descompune
numărul 16 16 este divizibil cu
2 obținem 8 8 de asemenea se împarte
la doi și obținem patru patrie
divizibil cu 2 2 împărțit la 2
va fi 1 16 este egal cu 2 la puterea
a patra iar ultimul număr 40 40
este divizibil cu doi de o are
c ultima cifră este 0 40 împărțit
la 2 este 20 20 de asemenea se
împarte la 2 20 împărțit la 2 este
10 de cel împărțim tot la 2 și
obținem 5 5 este divizibil cu 5
și rezultatul împărțirii va fi
140 este egal cu 2 la puterea a
treia ori 5 să aflăm acum Cel mai
mare divizor comun al numerelor
32 16:40 vom lua factorii comuni
la puterea cea mai mică observăm
că factorul comun este 2 iar exponentul
cel mai mic este 3 înseamnă că
vom scrie 2 la puterea a treia
Care este egal cu 8 iar cel mai
mic multiplu comun ai numerelor
32 16:40 va fi egal cu de data
aceasta luăm și factorii comuni
și ne comuni cu exponentul cel
mai mare adică 2 la puterea a cincea
ori 5 de la puse la puterea a 5-a
este chiar 32 ori 5 egal cu 160
am terminat punctul B merge mai
departe cu punctul C trebuie Să
descompunem numerele 42 și 54 îl
descompunem acum pe 42 42 este
divizibil cu 2 rezultatul împărțirii
este 21 21 este divizibil cu 3
iar rezultatul împărțirii este
7 ia 7 este divizibil cu 7 și rezultatul
împărțirii va fi 1 42 este egal
cu 2 ori 3 ori 7 mai departe Să
descompunem numărul 54 54 este
divizibil cu 2 54 împărțit la 2
este 27 27 este divizibil cu 3
de o are c suma cifrelor sale este
9 27 împărțit la 3 este 9 nu este
divizibil tot cu 3 3 este divizibil
cu 3 și obținem 154 este egal cu
2 ori 3 la puterea a treia cel
mai mare divizor comun al numerelor
42 și 54 este egal cu 2 ori 3 deoarece
2 și 3 sunt factorii comuni și
se vor lua acei factori la puterea
cea mai mică dirt 3 este egal cu
6 și acum Cel mai mic multiplu
comun al numerelor 42 și 54 vom
lua factorii comuni și ne comuni
cu exponentul cel mai mare adică
2 ori 3 la puterea a treia ori
7 2 ori 3 la puterea a treia este
27 ori 7 de 27 este 54 ori 7 puteam
să ne uităm direct la acest calcul
2 ori 3 la a treia aici în această
descompunere și puteam să scriem
direct 54 54 ori 7 șapte patru
este 28 cinci ori șapte este 35
și cu 237 Deci rezultatul va fi
378 continuăm cu punctul d trebuie
Să descompunem numerele 63 105
și 140 începem cu 63 63 nu este
divizibil cu 2 verificăm divizibilitatea
cu 3 deoarece suma cifrelor este
9 numărul va fi divizibil cu 3
63 împărțit la 3 este 21 21 se
împarte tot la trei și rezultatul
este 7 7 e divizibil cu 7 și obținem
163 egal cu 3 la puterea a doua
ori 7 să trecem acum la numărul
105 105 nu este divizibil cu 2
verificăm dacă este divizibil cu
trei dar a c suma cifrelor este
6 seamănă că numărul va fi divizibil
cu 3 105 împărțit la 3 este 35
35 nu este divizibil cu 3 de oarece
suma cifrelor este opt și opt nu
se împart exact la 3 am continuat
cu următorul număr prim 5 deoarece
ultima cifră este 5 înseamnă că
numărul se va împărțit la 5 35
împărțit la 5 este 7 iar 7 este
divizibil cu 7 105 se va Descompune
în trei ori cinci ori șapte continuăm
cu 140 140 este divizibil cu doi
de o are si ultima sa cifră este
0 140 împărțit la 2 este 70 70
este divizibil cu 270 împărțit
la 2 este 35 35 este divizibil
cu 5 35 împărțit la 5 este 7 140
va fi egal cu 2 la puterea a doua
ori cinci ori șapte cel mai mare
divizor comun al numerelor 63 105
și 140 va fi egal cu șapte deoarece
șapte este singurul factor comun
iar cel mai mic multiplu comun
al acestor numere va fi egal cu
Încercați să scrie factorii în
ordine crescătoare 2 la puterea
a doua ori 3 la puterea a doua
ori cinci ori șapte egal mai departe
cu 2 la a doua este 4 3 2 este
9 ori cinci ori șapte patru ori
nu este 36 5 ori 7 este 35 după
ce veți face alăturat calculul
o să obține un rezultatul 1260