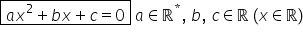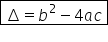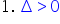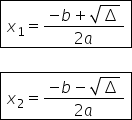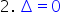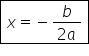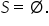Ecuații de gradul al doilea. Aplicații

să aplicăm acum formulele învățate

și să găsim soluția unor ecuații

de gradul al doilea cu o necunoscută

și mi se dă această ecuație 2x

pătrat adunat cu 6 x minus 9 egal

0 e clar că avem o ecuație de gradul

al doilea cu o necunoscută însă

Haideți să identificăm coeficienții

Deci dacă avem această formă a

x pătrat a donat cu b ori x adunat

cu c egal 0 Cât este A cât este

b și cât este ce Păi ca să ne fie

foarte clar cum Aici avem peste

tot adunare iar Aici avem adunare

și scădere Haide să rescriem prima

ecuație și avem 2x pătrat adunat

cu 6 x Deci aici avem și 6x și

aici putem să notăm adunat cu minus

9 egal cu 0 și acum chiar este

clar că A este 2 b este 6 iar ce

este minus 9 Deci aici la avem

pe a b este acesta care este egal

cu 6 iar c este atenție minus 9

si facem în continuare trebuie

să vedem cât este discriminantul

acestei ecuații Delta este egal

cu b pătrat scrie în formula minus

patru ace în cazul nostru Delta

este b este 6 Deci avem șase la

a doua minus 4 înmulțit cu a Care

este 2 4 x 2 înmulțit cu cei care

este minus 9 și acum calculăm Delta

ne dă 36 minus înmulțit cu minus

ne dă plus 4 x 2 8 ori 9 72 facem

suma și obținem 108 m este 108

este strict pozitiv Păi asta înseamnă

că avem două soluții care sunt

acestea Haide să scriem formula

x indice 1 2 vom avea la numitor

Avem doi ori iar la numărător avem

minus b plus sau minus radical

din Delta supra 2 ora și rezultă

x12 cu cât va fi egal cu cât vor

fi egal a b este 6 Dar de ce avem

aici minus 6 plus sau minus radical

din deltă care 108 supra Deci aici

avem 108 supra 2 înmulțit cu cât

este a a este tot 2 egal mai departe

cu linia de fracție avem minus

6 plus sau minus acum Trebuie să

scoatem de sub radical pe 108 fel

descompunem așa cum am tot fi putem

să privim direct aici avem 36 adunat

cu 72 înseamnă 2 ori 36 pe această

sumă ne dă 3 ori 36 Deci Haideți

să ștergem aici și vom nota alături

că 108 este trei ori 36 Când trecem

radicalul Deci vom avea radical

din acest produs palme obține radical

din 36 adică 6 ori radical din

3 plus 6 radical din 3 supra 4

Păi aici observăm că putem să dăm

factor comun pe șase și apoi putem

să simplificăm prin 2 că avem numitorul

4 sau putem să dăm factor comun

pe 2 și vom avea așa minus 3 plus

sau minus 3 radical din 3 închidem

paranteza supra 4 și acum putem

să simplificăm aici prin 2 și vom

avea aici unul și aici doi Deci

Rezultatul este să notăm numitorul

este doi și avem minus 3 plus sau

minus 3 radical din 3 pe 2 deci

soluția este formată din aceste

două elemente minus 3 plus sau

minus 3 radical din 3 pe 2 și cu

aceasta am încheiat am rezolvat

această ecuație următorul exercițiu

3 x la a doua minus x plus 8 egal

0 Haide să identificăm coeficienții

Deci dacă avem această formă a

x pătrat plus b ori x plus c egal

0 atunci aici ne apare semnul minus

Haide să scriem detaliat De ce

avem 3x pătrat pe minus x îl putem

scrie adunat cu minus unu ori x

adunat 8 egal cu 0 Deci aici se

vadă clar că avem opt egal 0 e

ușor de văzut că a ne dă 3 trece

mai și 3 b este egală cu un cu

minus unu Deci nu cu nuci cu minus

1 iar c este egal cu 8 să calculăm

discriminantul avem b pătrat minus

4-a orice Deci discriminantul este

egal cu b este minus 1 minus 1

totul la pătrat minus 4 înmulțit

cu ei adică cu 3 înmulțit cu c

care este 8 și avem că Delta este

aici avem 1 minus patru ordine

de 12 ori 8 ne dă 96 și obținem

1 minus 96 adică minus 95 Ce fel

de număr este 95 este strict negativ

asta înseamnă că soluția acestei

ecuații este mulțimea vidă cu alte

cuvinte nu există nici un număr

real care să verifice această relație

ultimul exemplu 25 ori x la a doua

adunat cu 10 ore x adunat cu 1

este egal cu 0 și aici avem tot

o ecuație de gradul al doilea Haide

să identificăm coeficienții Deci

dacă avem a x pătrat adunat cu

b ori x adunat cu c egal 0 atunci

e ușor de văzut că a este 25 b

este egal cu 10 iar c este egal

cu 1 pe calculăm discriminantul

Delta avem b pătrat minus 4 AC

Deci vom obține Delta egal cu b

este 10 Deci avem 10 la a doua

minus 4 înmulțit cu a este 25 iar

c este 1 Deci vom obține Delta

egal cu 100 minus aici obținem

tot 100 Păi asta înseamnă că discriminantul

este în această situație 0 cu alte

cuvinte vom obține o soluție și

haide să scriem formula soluția

este minus linie de fracție b supra

2-a rezultă că x Cu cât este egal

minus și înlocuim Deci avem aici

linie de fracție b este 10 Deci

trecem aici în 10 supra 2 înmulțit

cu ei este 25 de 2 ori 25 rezultă

mai departe că vom obține avem

10 supra 50 simplificăm prin 10

scriem direct 1 supra 5 Deci soluția

acestei ecuații este minus 1 supra

5 această ecuație Haide să o vedem

Alături o puteam mă rezolva și

în clasa a șaptea fără să folosim

vreun discriminant sau vreo formulă

de aici de ce Puteam să facem acest

lucru pentru că ea de aici avem

de fapt pătratul unei sume pentru

că putem scrie 25 x pătrat întrecem

5 x totul la a doua pe unu îl putem

scrie 1 la pătrat aici avem adunare

la fel și aici și aici avem 2 înmulțit

cu 5 x înmulțit cu 1 adică ne dă

10 x egal cu zero Păi da rezultă

că avem de fapt 5 x plus 1 totul

la pătrat egal 0 echivalent cu

a spune că 5 x plus 1 ne dă 0 Deci

x este egal cu minus 1 supra 5

exact ce am obținut și aici soluția

fiind minus 1 supra 5 prin urmare

Haide să reținem că la modul general

când vrem să rezolvăm o ecuație

de gradul al doilea trebuie să

cunoaștem formula pentru determinarea

discriminantul lui precum și formulele

pentru determinarea necunoscute