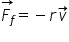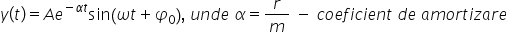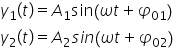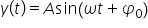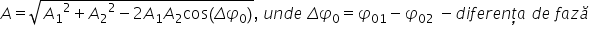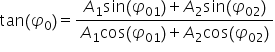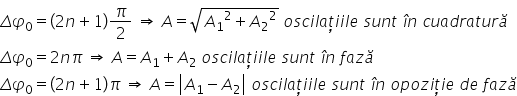Forţa rezistivă. Amortizarea oscilaţiilor. Compunerea oscilaţiilor paralele.

În ce an a treia Lecție despre

oscilații și unde mecanice vom

discuta despre oscilațiile amortizate

și despre compunerea oscilațiilor

paralele oscilațiile amortizate

ale unui oscilator întrun medium

au loc datorită forțelor de frecare

dintre o și la torul respectiv

și mediul de obicei de tip Fruit

prin care el se mișcă această forță

de frecare este prezentat în această

ecuație Ea este proporțională cu

viteza de mișcare și bineînțeles

se opune acestei mișcări de aceea

are sensul minus Constanța de proporționalitate

dintre forța de frecare și viteză

se notează cu iar și ia depinde

de geometria de forma o și la torului

și de natura mediului prin care

are loc oscilația Cât de vâscos

este acest meci odată ce avem o

formulă pentru forța de frecare

putem scrie formula fundamentală

a dinamicii Care este masa ori

accelerația egală cu Forțele care

acționează în cazul oscilator armonic

avem o forță de tip pe elastic

Care este minus ca înmulțită cu

melodia oscilației plus această

nouă forță de frecare care acționează

și asupra corpului această ecuație

poate fi rescrisă în felul următor

pentru a fi rezolvată Deci trecând

în partea stângă a ecuației toți

membrii din partea dreapta avem

cai y Care este o funcție de timp

bineînțeles plus nervi dar viteza

prin definiție este Delta Delta

yu6 împărțit la Delta t m viteza

este variația Lunca ții în unitatea

de timp și na mai rămas M A deci

plus m ori accelerația pe care

voi in felul urmator Delta variația

dublă elongații împărțită la timp

egal cu zero bineînțeles pentru

Delta tinde la 0 aceasta acest

tip de ecuație nu ați mai văzut

încă o scriu numai întrecere fără

a face nicio demonstrație din ea

numai pentru a vă sugera Cum putem

extrage dintre astfel de ecuație

ecuația pentru de te deci am și

simplu scrie viteza ca variația

lui y ca funcție de timp iar accelerația

Care este variația vitezei va fi

variația dublă a alunga Asiei în

raport cu timpul această cantitate

o vinde column când veți face calcul

diferențial acestea sunt diferentiale

de ordinul întâi și ordinul doi

derivate de ordin întâi și ordinul

doi ale wrong Asiei Nu nu le știți

încă dar numai ca să vedeți cum

se rezolvă această ecuație pe scurt

avem o ecuație diferențială de

ordinul doi în care singura necunoscută

este yyy8 II ca funcție de timp

dar din nou aceasta este doar un

comentariu Nu trebuie să știți

deocamdată aceste lucruri dar în

felul acesta se rezolvă în calculul

diferențial această ecuație obținem

următoarea soluție nația ca funcție

de timp va fi o amplitudine înmulțită

cu o funcție exponențială e la

minus al fateh și înmulțită apoi

cu o funcție sinusoidală de timp

De ce avem în funcția sinusoidală

tipică cu care suntem obișnuiți

pentru o mișcare oscilatorie armonică

dar în particular pentru oscilații

amortizate avem în amplitudine

un factor de pandant de timp această

exponențial dacă Reprezentăm grafic

această funcție am uitat să definesc

Alfa Deci Alfa coeficientul exponențial

a din din această formulă este

definit ca raportul dintre R și

2 m b c Constanța din de proporționalitatea

forței de frecare și m este masa

oscilatorului Deci Alpha este definit

ca aer împărțit la 2 m și se numește

coeficient de amortizare după când

spuneam dacă Reprezentăm grafic

această soluție pentru elongația

unei oscilații armonice amortizate

obținem această formă de ce nu

verde cu culoarea verde obținem

sau desemnăm această valoare a

lui y de tip ca funcție de timp

bineînțeles cu roșu punct întrerupt

cu linie roșie întreruptă în am

desenat doar funcția din fața funcției

sinus Deci cu roșu avem A e la

minus Alpha Tec o funcție care

scade exponențial în timp ia se

numește anvelopa oscilații și după

cum ne așteptăm în vedem că vedem

Că întradevăr avem o funcție sinusoidală

Deci avem o oscilație periodică

dar efectul amortizării apare în

este de scris de această anvelopă

ce scade exponențial în care vedem

că amplitudinea aceste oscilații

scade în timp Nici acesta este

efectul forței de frecare care

duce la oscilații amortizate amplitudinea

scade în timp exponențial după

această lege oscilațiile sunt de

mai multe tipuri din acest punct

de vedere primul tip bineînțeles

este cel discutat până acum cel

al oscilațiilor libere sau ne disipative

în care nu avem forțe de frecare

sau disipative care pot amortiza

oscilația în acest tip de oscilație

energia totală se conservă după

cum am văzut în lecția trecută

bineînțeles și alte al doilea tip

este cel.ro și la ți lor amortizate

pe care le am discutat acum care

se mai numesc și disipative pentru

că energia totală se consumă Deci

oscilatorul încetează energie mediului

cu care interacționează prin forța

de frecare iar al treilea triptip

de oscilații este cel al lui și

lați lor forțate sau întreținute

despre care vom mai discuta în

curând și în care furnizăm energie

din exterior pentru compensarea

pierderilor deci oscilațiile sunt

amortizate în acest caz sau ar

fi amortizate pentru că există

o forță de frecare semnificativă

dar noi furnizăm din exterior pentru

o anumită metodă energia care sar

consuma și se consumă și felul

acesta păstrăm energia totală a

oscilatorului constantă obținând

un tip de oscilație caracteristicelor

libere Dar bineînțeles având în

același timp o disipare de energie

aceste aceste de oscilații se numesc

forțat sau întrețin să mergem acum

la compunerea oscilațiilor paralele

Deci Considerăm 25 armonice care

sunt paralele în sensul că forțele

elastice au aceeași direcție precum

vedem în această schemă Deci ce

vedem este un corp care este atașat

la două resorturi și bineînțeles

el Atunci este supus la două forțe

elastice care produc elongații

complementare Adică când unul din

resort se întinde celelalte strânge

și Deci forțele elastice au sensuri

opuse dar au aceeași direcție și

presupunem pentru simplicitatea

calculelor că frecvențele proprii

ale celor două resorturi sunt egal

vă reamintesc Omega este egal cu

radical din ca pe m asta înseamnă

că cele două resorturi au aceeași

constantă elastică Haideți să calculăm

în acest caz ecuațiile mișcării

acestui oscilator format compus

format din două și la soare Deci

plecăm de la ecuația pentru fiecare

elongație pentru fiecare din cele

două resorturi cel 27 are în care

am pus condiția ca frecvențele

să fie sau pulsatiile să fie egal

în lecția 6 de curent alternativ

am studiat proprietățile funcțiilor

sinusoidale Deci Haideți să scriu

undeva lecția 6 de curent alternativ

vreau pe care vă invit soare vedeți

acolo am demonstrat că atunci când

adunăm două funcții sinusoidale

obținem tot o funcție sinusoidală

de aceeași Pulsar Deci elongația

mișcării oscilatorii compuse va

fi a sinus de omega-3 plus și 03

pentru a o Descrie complet trebuie

să calculăm a amplitudinea și fie

0 pentru aceasta folosind diagrama

fazorială Deci aceasta este diagrama

fazorială a acestor mișcări oscilatorii

Deci vectorul sau vectorul A1 descrie

elongația y1a 2 descrie elongația

y2 și bineînțeles suma lor vectorială

Deci A1 plus A2 adunate vectorial

va reprezenta fazorul a Ce descrie

elongația mișcării oscilatorii

compuse deci tot ce trebuie să

faci este să fac să calculăm proprietățile

aceste sume vectoriale a 2 fazori

A1 și A2 pentru aceasta proiectăm

această ecuație pe cele două axe

când proiectăm ecuația vectorială

această ecuație vectorială pe axa

o x obținem următoarea ecuație

a cosinus de fi 0 este egal cu

a 1 cosinus de fi 0 1 plus a 2

cosinus de 0 2 meci pentru fiecare

Vector calculăm proiecția și bineînțeles

proiecția va fi dată de cosinusul

unghiului la fel pe o putem scrie

că a ținut deschis 0 este egal

cu a 1 sinus de pi zero unu plus

A2 sinus de 0 2 observăm că dacă

împărțim a doua ecuații la prima

ecuație una din cele două necunoscute

și anume amplitudinea se simplifică

și rămâne încă o singură necunoscută

și zeci obținem ecuația pentru

fi 0 și anume că tangentă de fi

0 sinus împărțit la cosinus tangentă

egală cu raportul dintre mărimile

din dreapta acestor Două ecuații

pentru a calcula magnitudinea a

folosim următoarea identitate trigonometrică

și anume că între un triunghi și

anume În cazul acesta în acest

triunghi dacă notăm cu unghiul

teta unghiul opus laturii a și

bineînțeles această latură va fi

A1 putem scriu următoarea ecuație

a pătrat este egal cu a 1 pătrat

plus A2 pătrat minus 2 a 1-a 2

cosinus de data aceasta este o

ecuație general valabilă între

Laturile unui triunghi și unghiul

opus laturii a în cazul acesta

putem însă observa că unghiul teta

Care este acest unghi meci teta

este acest unghi teta este egal

cu 180 de grade minus unghiul Delta

fi Deci notăm unghiul dintre fazori

iau 1 și a 2 cu Delta fii sau Delta

fi 0 mai exact și atunci unghiul

teta este egal cu 180 de grade

sau pai Radian minus dar dar știm

că cosinus de Deci în concluzie

cosinus de tata este egal cu cosinus

de pi minus Delta fi Care este

egal cu minus cosinus de Delta

fii cosinus de 180 de grade minus

unu unghi Alfa este minus cosinus

de a fost o relație generală în

care după cum am spus Delta fizzer

definit ca și zero unu minus fie

zero doi zece am introdus această

nouă mărime și în concluzie putem

înlocui minus cosinus de teta cu

cosinus de Delta fie 0 și obținem

pentru magnitudinea sau Maximul

lui amplitudinea lui elongație

compuse următoarea ecuație radical

din 1 pătrat plus A2 pătrat plus

doi a 1-a 2 cosinus Delta fie 0

unde Delta fie zero este fie zero

unu minus și zero doi și felul

acesta am obținut ecuațiile pentru

elongația mișcării oscilatorii

compuse în acest caz paralele de

aceeași frecvență Haideți să vedem

proprietățile A deci aceasta este

cu ață pentru amplitudinea și avem

următoarele cazuri particulare

în cazul în care Delta fi 0 care

din nou este prin definiție fie

zero unu minus fie zero doi În

cazul în care acest unghii relativ

inițial este un multiplu impar

de 90 de grade în acest caz cosinusul

va fi 0 oscilațiile se numesc în

cuadratură pentru că cosinusul

Pfizer obține imediat că am Pitu

din ea este egal cu radical din

suma pătratelor altitudinii de

individuale de aici numele de cuadratură

un alt caz particular este acela

un și relațiilor în fază în care

Delta fi 0 este cu multiplu par

de 180 de grade adică 0 367 departe

în acest caz cosinus de 0 este

egal cu plus unu și atunci obținem

a unui pătrat plus A2 pătrat plus

2 1 2 care este a 1 sau 2 la pătrat

Deci obținem că în acest caz amplitudine

este suma pietonilor și de individuale

și de aceea oscilație se numesc

în față și bineînțeles avem cazul

opus oscilațiile în opoziție de

fază în care Delta fi 0 este o

multiplu impar de pe adică 180

de grade 270 de grade 180 de grade

3 ori 180 de grade și așa mai departe

cest caz cosinus de Delta fie zero

va fi minus unu judeci obținem

a unui pătrat plus a 2 pătrat minus

2 a1 a2 Care este 1 minus 2 la

pătrat judeci în acest caz amplitudinea

oscilației compuse este modulul

diferenței dintre amplitudinea

oscilațiilor individuale Acestea

fiind cazurile particulare mai

important ale oscilațiilor compuse

paralele oscilațiile paralele cu

amplitudini egal și faze inițiale

nule Haide să discutăm despre acest

caz pentru că vom vedea în lecția

viitoare când vom discuta despre

bătăi în oscilații Cum anume acest

caz este relevant Deci Considerăm

amplitudine gali și faze inițiale

nu lipsesc în acest caz Care este

un caz de simplificat avem următoarele

Două ecuații pentru elongații individuale

y1 este a sinus de Omega 1 t y

2 este a sinus de Omega 2 t de

cină cest caz avem frecvențe sau

pulsații proprii diferite dar celelalte

celelalte doi parametri ai oscilației

și anume altitudinea sunt egali

în cazul faze și egal cu 0 șunca

simplificat totuși în care ne îndreptăm

către discuția situații în care

pulsatiile nu sunt egale bun în

acest caz putem scrie Bineînțeles

că y de ten Care este suma celor

două este egal cu a înmulțit cu

sinus de Omega 1 t plus sinus de

Omega 2 t ere apoi face apel sau

folosim următoarele următoarele

identitate trigonometrică sinus

de Alfa plus sinus de B este egal

cu 2 cosinus de Alfa minos Betta

împărțit la 2 sinus de Alfa plus

Betta împărțit la 2 judeci în concluzie

dacă notăm cu o anumită valoare

un anumit parametru această cantitate

și anume notăm cu Delta Omega Omega

1 minus Omega 2 împărțit la 2 și

cu Omega Omega 1 plus Omega 2 împărțit

la 2 obținem următoarele ecuații

pentru inundația oscilație compuse

ai de te va fi 2 înmulțit cu a

cosinus de Delta Omega adică diferența

împărțită la 2 înmulțit cu test

sinus de Omega adică sumă am pățit

la 2:00 munții tăcute