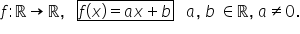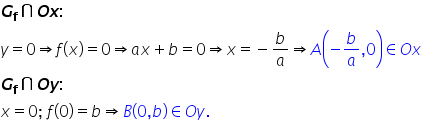Funcția de gradul I (aplicații)

în această lecție vom face câteva

reprezentări grafice ale unor funcții

definite pe ramuri iar la final

mod studia monotonia unei funcții

de gradul întâi și începem cu acest

exercițiu mai simplu să ceri să

Reprezentăm grafic funcția f definită

pe r cu valori in r f de x egal

cu minus x plus 3 Dacă x este mai

mic sau egal cu 0 și 1 dacă x este

mai mare ca 0 nu face mai întâi

tabelul de Valori avem x de la

minus infinit la plus Infinit din

moment ce funcție este definită

pe ramuri vom trece separat în

tabel cele două forme ale funcției

Așadar pe această linie avem funcția

f de x egal cu minus x plus 3 iar

apoi f de x egal cu 1 vom calcula

valorile funcției pentru x egal

cu 0 trecem în tabel în special

valoarea 0 de la care funcția și

Schimbă forma pentru x egal cu

0 calculăm valoarea funcției minus

x plus 3 avem 0 plus 3 egal cu

3 această funcție nu este definită

pentru x mai mare ca 0 prin urmare

putem să bem această zonă iar punctul

de coordonate 03 aparține graficul

și mai avem nevoie de încă un punct

pentru a trasa În graficul acestei

funcții alegem x egal cu minus

unu iar pentru x egal cu minus

1 f de x este minus minus unu Adică

1 plus 3 4 Așadar pentru prima

funcție pentru prima forma a funcției

am găsit punctele a de coordonate

0 3 și b de coordonate minus 1

și 4 și acum Avem nevoie de alte

două puncte pentru f de x egal

cu 1 vom considera că în x egal

cu zero funcția ia valoarea 1 chiar

dacă această funcție nu este definită

pentru x egal cu zero vom considera

că în punctul 0 funcția este egală

cu 1 Iar acest punct de coordonate

0 1 nu aparține graficului funcției

Așadar vom pune aici o paranteză

rotundă și mai avem nevoie de încă

o valoare pentru a reprezenta grafic

această funcție de exemplu pentru

x egal cu 2 f de x este 1 funcția

nu e Avalor pentru x mai mic ca

0 Așadar putem să furăm această

zonă și am obținut punctul C de

coordonate 0 1 și d de coordonate

2 1 și acum Reprezentăm cele patru

puncte între un sistem de axe x

o y avem punctul A de coordonate

0 3 Iată Aici este punctul a b

de coordonate minus unu patru Aici

este punctul B C de coordonate

0 1 și d de coordonate 2 1 aici

avem punctul D pentru a obține

graficul funcției f de x egal cu

minus x plus 3 unim punctele a

și b obținem astfel o semidreaptă

Yato punctul A de coordonate 0

3 aparține graficului funcției

așa dar aici o să avem o paranteză

dreaptă iar pentru a reprezenta

grafic funcția f de x egal cu unu

o să unim punctele c și d punctul

C de coordonate 0 1 1 aparține

graficului Așadar vom avea aici

o semidreaptă deschisă continuăm

cu al doilea exercițiu Iată avem

funcția f definită pe r cu valori

in r f de x egal cu minus 2x minus

1 dacă x este mai mic decât minus

2 și 4 x plus 3 Dacă x este mai

mare sau egal decât minus 2 facem

tabelul de valori avem x de la

minus infinit la plus infinit trecem

în tabel cele două forme ale funcției

f de x egal cu minus 2x minus 1

și f de x egal cu 4 x plus 3 trecem

în tabel mai întâi valoarea minus

2 de la care funcția își schimbă

forma pentru prima lege a funcției

f de x egal cu minus 2x minus 1

vom calcula valoarea acesteia în

punctul minus 2 f de minus doi

va fi 4 minus unu adică trei și

mai Considerăm încă o valoare mai

mică ca minus 2 de exemplu minus

3 iar f de minus 3 va fi 6 minus

1 5 punctul de coordonate minus

2 3 nu aparține graficului funcției

așa dar o să avem o paranteză rotundă

chiar dacă funcția nu este definită

pentru x egal cu minus doi Am calculat

totuși valoare a funcției ca să

vedem comportamentul acesteia la

capătul intervalului însă din moment

ce x este mai mic strict de minus

doi vom pune aici o paranteză rotundă

și vom considera că punctul de

coordonate minus 2 3 nu aparține

graficului funcției această funcție

minus 2x minus unu nu este definită

pentru valori mai mari ca minus

doi așa dar putem să faci urăm

această porțiune și acum calculând

valoarea funcției f de x egal cu

4 x plus 3 pentru x egal cu minus

doi avem minus 8 plus 3 minus 5

punctul de coordonate minus 2 minus

5 aparține graficului funcției

Așadar avem aici o paranteză dreaptă

Și mai luăm un cu o valoare mai

mare decât minus 2 0 f de 0 va

fi 3 această funcție 4x plus 3

nu este definită pentru valori

mai mici decât minus 2 așadar am

obținut punctele a de coordonate

minus 2 3 b de coordonate minus

3 5 acestea sunt pentru prima forma

a funcției apoi C de coordonate

minus 2 minus 5 și d de coordonate

03 Reprezentăm aceste puncte între

o sistem de axe a de coordonate

minus 2 3 aici avem punctul a b

de coordonate minus 3 5 Aici este

punctul B C de coordonate minus

2 minus 5 Aici este minus cinci

aici avem punctul c și d de coordonate

0 și 3 Aici este punctul de graficul

funcției f de x egal cu minus 2x

minus unu va fi o semidreaptă Yato

punctul A de coordonate minus 2

3 nu aparține graficului funcției

Așadar aici avem o paranteză rotundă

iar pentru funcția f de x egal

cu 4 x plus 3 avem celelalte două

puncte c și d funcția ia valori

mai mari ca minus 2 Așadar graficul

acesteia va fi situat în partea

dreaptă a lui minus doi Deci în

acest semiplan iar graficul este

obține unind punctele c și d punctul

C de coordonate minus 2 minus 5

aparține graficului Deci aici avem

o paranteză dreaptă vă spuneam

în lecția trecută că monotonia

funcției de gradul întâi este dată

de semnul lui a Iată pentru prima

funcție a este minus 2 Așadar negativ

prin urmare funcția este descrescătoare

Iată această semidreaptă coboară

iar pentru funcția f de x egal

cu 4 x plus 3 coeficientul lui

x este pozitiv prin urmare funcția

este crescătoare Deci semidreapta

aceasta urcă următorul exercițiu

plăcere să Reprezentăm grafic funcția

f definită pe r cu valori in r

f de x egal cu 2x dacă x este mai

mic decât minus 1 minus 3x plus

patru dacă x aparține intervalului

minus 1 1 și 4 x minus 2 dacă x

este mai mare sau egal decât 1

facem tabelul de valori avem x

de la minus infinit la plus infinit

prima funcție f de x egal cu 2x

apoi f de x egal cu minus 3x plus

4 și f de x egal cu 4 x minus 2

trecem în tabel mai întâi valorile

acesteia de la care funcția își

schimbă forma minus unu și unu

funcția f de x egal cu 2x nu este

definită pentru x egal cu minus

unu totuși vom calcula valoarea

funcției pentru minus 1 asa vedem

comportamentul funcției la capătul

intervalului Așadar f de minus

1 este minus 2 apoi mai Alege o

valoare pentru x mai mică decât

minus 1 de exemplu minus 2 f de

minus 2 va fi minus 4 punctul de

coordonate minus 1 minus 2 nu aparține

graficului funcției Așadar vom

pune o paranteză rotundă și funcția

nu este definită pentru valori

mai mari decât minus 1 trecem la

a doua formă a funcției avem f

de x egal cu minus 3x plus patru

din moment ce ixia valori cuprinse

între minus 1 și 1 putem să furăm

zona din afara acestui interval

f de minus unu va fi minus trei

ori minus unu adică trei plus 47

iar aici vă pun eu paranteză dreaptă

Pentru că x poate lua valoarea

minus unu Deci punctul de coordonate

minus 1 7o să aparține graficului

funcției iar pentru x egal cu 1

avem minus 3 plus 4 1 1 nu aparține

acestui interval prin urmare nici

punctul de coordonate 1 1 nu o

să aparțină graficului funcției

Așadar vom pune aici o paranteză

rotundă apoi avem funcția f de

x egal cu 4 x minus 2 Pentru x

egal cu 1 avem patru minus doi

doi funcția lui Avalor pentru x

mai mic ca 1 Așadar o să faci urăm

această porțiune și mai alegem

în cu o valoare mai mare decât

unul de exemplu 2 iar f de 2 este

8 minus 2 6 din moment ce x poate

lua și valoarea 1 aici o să avem

o paranteză dreaptă așadar am obținut

următoarele puncte a de coordonate

minus 1 minus 2 b de coordonate

minus 2 minus 4 C de coordonate

minus 1 7 D de coordonate 1 1 și

e de coordonate 1 2 f de coordonate

2 6 Poate că era mai bine dacă

le scriam mai jos avem punctul

A de coordonate minus 1 minus 2

Iată Aici este punctul a b de coordonate

minus 2 minus 4 Aici este minus

4 aici avem punctul B C de coordonate

minus unu șapte unu doi trei patru

cinci șase șapte aici avem punctul

c D de coordonate 1 1 Aici este

punctul d a de coordonate 1 2 este

coordonate 2 și 6 Iată Aici este

punctul f și acum să trasăm prima

semidreaptă un in punctele a și

b pe prima ramură am avut funcția

f de x egal cu 2x această funcție

este crescătoare acesta este graficul

funcției iar Aici avem o paranteză

rotundă pentru că punctul de coordonate

minus 1 2 nu aparține graficului

funcției aici era punctul A și

aici punctul b graficul funcției

minus 3x plus 4 va fi un segment

acesta se obține unind punctele

c și d punctul de coordonate minus

1 7 aparține graficului Deci aici

o să avem o paranteză dreaptă iar

punctul de coordonate 1 1 nu aparține

graficului așa dar aici vom avea

o paranteză rotundă iar la final

trebuie să mai Reprezentăm grafic

funcția f de x egal cu 4 x minus

2 punctul de coordonate 1 2 adică

punctul E aparține graficului avem

iarăși o funcție crescătoare Deci

această semidreaptă urcă iar aici

o să avem o paranteză dreaptă am

terminat cu graficele mai avem

un ultim exercițiu în care studiem

monotonia unei funcții Studiați

monotonia funcției f definită pe

r cu valori in r f de x egal cu

3-a minus 6x minus 5 unde m este

un parametru real vă spuneam în

lecția trecută că monotonia funcției

de gradul întâi depinde de semnul

lui a a este coeficientul lui x

în acest caz a este 3-a minus 6

dacă a este pozitiv funcția este

strict crescătoare iar dacă a este

negativ funcția este strict descrescătoare

Așadar monotonia funcției depinde

de semnul lui A iar în acest caz

a este egal cu 3-a minus 6 Așadar

vom avea două situații posibile

în primul caz Dacă 3-a minus 6

este pozitiv adică 3 m este mai

mare ca 6 asta înseamnă că m este

mai mare ca 2 în această situație

m aparține intervalului 2 infinit

iar funcția este strict toare și

a doua situație posibilă Dacă 3-a

minus 6 este negativ adică 3 m

este mai mic decât 6 m aparține

intervalului minus Infinit 2 în

această situație funcția este strict

descrescătoare nu studiem cazul

în care m este egal cu 2 pentru

că dacă Ema și egal cu 2 se anulează

Termenul care îl conține pe x și

nu mai avem o funcție de gradul

întâi avem o funcție constantă