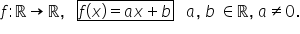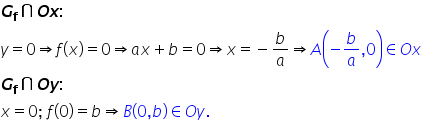Funcția de gradul I: graficul și monotonia (teorie)
Tag-uri
Partajeaza in Google Classroom

Transcript
salut în lecția aceasta o să discutăm
despre Funcția de gradul întâi
despre graficul acesteia și monotonia
o funcție f definită pe r cu valori
in R de forma f de x egal cu ax
plus b unde a și b sunt numere
reale se numește funcție a fină
iar dacă a este diferit de 0 atunci
se obține Funcția de gradul întâi
se numește așa deoarece x este
la puterea întâia numerele a și
b se numesc coeficienți iar o funcție
de gradul întâi este bine determinată
dacă se cunosc acești coeficienți
a și b ecuația ax plus b egal cu
0 se numește ecuația atașată funcției
graficul unei funcții de gradul
întâi este o dreaptă noi știm că
o dreaptă este bine determinată
dacă se cunosc două puncte Așadar
pentru a reprezenta geometric graficul
unei funcții de gradul întâi vom
alege două valori arbitrare pentru
x și apoi calculăm valorile funcției
uneori însă e De preferat să tras
în graficul funcției de gradul
întâi obținând punctele de intersecție
cu axele o x și o y să vedem în
exemplu avem funcția f definită
pe r cu valori in r f de x egal
cu 2x minus 5 pentru a obține punctul
de intersecție dintre graficul
funcției și axa o x Compune condiția
ca e să fie egal cu 0 asta înseamnă
că f de x este zero rezolvăm ecuația
atașată 2x minus 5 egal cu 0 și
obținem x egal cu 5 supra 2 Așadar
punctul de intersecție dintre graficul
funcției și axa o x va fi punctul
A de coordonate 5 supra 2 0 pentru
a obține acum punctul de intersecție
dintre graficul funcției și axa
o y în pune ea ca abscisă să fie
egală cu zero Așadar x este egal
cu 0 iar ordonata se obține calculând
f de 0 f de 0 este egal cu 2 ori
0 minus 5 și y egal cu minus 5
Prin urmare avem punctul b de coordonate
0 și minus 5 și acum haide să Reprezentăm
grafic această funcție într un
reper cartezian punctul A de coordonate
5 supra 2 0 5 pe 2 este 2 iar Aici
este punctul A de coordonate 5
pe 2 0 și b de coordonate 0 și
minus 5 aici avem punctul B un
in cele două puncte se obține graficul
funcției f Iată această metodă
de a trasati graficul funcției
obținând punctele de intersecție
dintre graficele o x și o y care
unele avantaje de exemplu atunci
când se cere să determinăm aria
triunghiului obținut de graficul
funcției f și axele o x și o y
folosind această metodă putem determina
rapid lungimile catetelor o a respectiv
OB să discutăm în continuare despre
câteva cazuri particulare ale funcțiilor
de formă a x plus b în cazul în
care b este egal cu 0 obținem funcția
f de x egal cu ax graficul aceste
funcții este o dreaptă care trece
prin origine aici întâlnim două
situații particulare dacă a este
egal cu 1 se obține funcția f de
x egal cu x graficul aceste funcții
este o dreaptă care trece prin
origine Haideți o trasăm ia atât
dacă x este egal cu 1 atunci f
de x este egal cu 1 Deci avem punctul
de coordonate 1 1 dacă x este egal
cu 2 f de x este 2 Așadar obținem
punctul de coordonate 2 2 apoi
avem punctul de coordonate 3 3
4 4 și așa mai departe dreapta
astfel obținută iatom este de fapt
bisectoarea unghiului x o y de
aceea această dreaptă se mai numește
prima bisectoare o altă situație
particulară dacă a este egal cu
minus unu atunci obținem funcția
f de x egal cu minus x Iată pentru
x egal cu 1 f de 1 este minus 1
Deci avem punctul de coordonate
1 minus 1 dacă x este 2 f de x
este minus 2 Deci avem punctul
de coordonate 2 și minus 2 apoi
avem punctul de coordonate 3 și
minus 3 Iată un indus este puncte
se obține o altă dreaptă această
dreaptă este bisectoarea unghiului
y este a unghiului x o y prim și
ia se mai numește a doua bisectoare
și un alt caz particular al funcțiilor
de forma f de x egal cu ax plus
b este cazul în care a este egal
cu 0 în această situație se obține
funcția f de x egal cu b iar această
funcție se numește funcție constantă
iar graficul este o dreaptă paralelă
cu Axa o x care trece prin punctul
de coordonate 0 b Iată Dacă punctul
b este undeva aici atunci toate
valorile funcției sunt egale cu
b prin urmare graficul va fi O
dreaptă paralelă cu Axa o x care
trece prin punctul de coordonate
0 b și în continuare vreau să discutăm
puțin despre monotonia funcției
de gradul întâi fie funcția f definită
pe r cu valori in R Unde f de x
este egal cu ax plus b a și b numere
reale a diferit de 0 alegem două
valori arbitrare X1 și X2 numere
reale astfel încât x 1 să fie mai
mic decât x 2 știind că monotonia
unei funcții se poate studia stabilind
semnul raportului R egal cu f de
x 1 minus f de x 2 supra x 1 minus
x 2 acesta se mai numește raportul
de variație asociată funcției f
Haideți să calculăm acest raport
fdx 1 buc engle cu ax1 plus b iar
e de x 2 este egal cu a x 2x plus
b supra x 1 minus x 2 desfacem
paranteză și de factor comun pe
a avem A pe lângă x 1 minus x 2
iar b cu minus b se reduce și la
numitor avem x 1 minus x 2 observăm
că se simplifică x 1 minus x 2
și final de rămâne a observăm Așadar
că semnul acestui raport depinde
de A dacă A este un număr pozitiv
atunci raportul este pozitiv iar
funcția va fi strict crescătoare
iar dacă a este negativ atunci
raportul de variație asociat funcției
va fi negativ prin urmare funcția
va fi strict descrescătoare așa
dar e foarte important să reținem
că monotonia funcției de gradul
întâi depinde de semnul lui A dacă
A este pozitiv funcția este strict
crescătoare iar dacă a este negativ
funcția este strict descrescătoare
de exemplu funcția f definită pe
r cu valori in r f de x egal cu
minus radical din 2 x plus 5 este
o funcție strict descrescătoare
pentru că a este negativ iar f
de pe r cu valori in r f de x egal
cu 3 pe 4 x plus 9 va fi o funcție
strict crescătoare pentru că a
este pozitiv