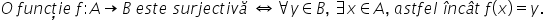Funcții surjective

bun considera o funcție de prezentată

printr o diagramă care Asociază

unor elevi media anuală la finalul

clasei a 10-a astfel Vlad are media

850 Radu a remedia 970 Maria are

media 10 și Oana are media 10 mulțimea

b se numește codomeniul funcției

sau mulțimea în care funcția ia

valori trebuie să facem distincția

între mulțimea în care funcția

ia valori și mulțimea valorilor

funcției În exemplul de față imaginea

funcției sau mulțimea valorilor

funcției este mulțimea formată

din numerele 850 971 merele minus

2 și 100 nu fac parte din imagini

a funcției întrucât ele nu pot

fi mediile unor elevi în general

imaginea unei funcții este inclusă

în codomeniu dar există și funcții

pentru care imaginea coincide cu

codomeniul aceste elemente din

b care nu sunt imaginile nici unui

argument din ei vor face diferența

dintre o funcție surjectivă și

o funcție surjectivă astfel o funcție

f definită pe a cu valori în b

este surjectivă sau surjectiv dacă

pentru orice element din b există

un x din a astfel încât f de x

egal cu y mai putem spune cu o

funcție este surjectivă Dacă F

de ei sau imaginea funcției coincide

cu codomeniul În exemplul de față

această funcție nu este surjectivă

Haideți să vedem în continuare

un exemplu de funcție surjectivă

Să considerăm funcția f definită

pe r cu valori in r f de x egal

cu 3 x plus 5 trebuie să verificăm

dacă pentru orice x y numere al

există un x din a r astfel încât

f de x să fie egal cu y a studia

surjectivitatea unei funcții înseamnă

a rezolva ecuația f de x egal cu

y dacă această ecuație are cel

puțin o soluție atunci funcția

este surjectivă în caz contrar

funcția nu este surjectivă Așadar

va trebui să rezolvăm ecuația 3x

plus 5 egal cu y obținem x egal

cu y minus 5 supra 3 Dacă x este

număr real ales în mod arbitrar

atunci și y minus 5 supra 3 va

fi număr real în consecință această

funcție este surjectivă putem să

facem și eu o scurtă verificare

pentru a vedea dacă această valoare

obținută este întradevăr soluție

a ecuației f de x egal cu y și

atunci Am calculat dx avem f de

minus 5 supra 3 înlocuim această

valoare în formula de mai sus și

obținem trei ori Y plus 5 supra

3 plus 5 se simplifică 3 minus

5 plus 5 este egal cu y a arătat

Așadar că pentru orice a y pe mulțimea

numerelor întregi cu valori în

mulțimea numerelor întregi este

de x egal cu 3 x plus 5 am ales

să o funcție care are aceeași formulă

pași mai sus însă domeniul și codomeniul

este mulțimea numerelor întregi

dacă rezolvăm ecuația 3x plus 5

egal cu y obținem x egal cu y minus

5 supra 3 trebuie să verificăm

dacă oricare ar fi Y apartamente

3 este număr întreg să luăm câteva

exemple Dacă y este 5 atunci x

este 5 minus 5 supra trei adică

zero întradevăr x este număr întreg

dacă alegând să intre că egal cu

0 atunci x va fi minus 5 supra

3 dar această valoare nu este număr

întreg în consecință nu pentru

orice y2j ales în mod arbitrar

această ecuație are soluție în

z în consecință funcția aceasta

nu este surjectivă există și o

metodă grafică prin care putem

studia surjectivitatea și anume

dacă orice paralelă la axa o x

dusă prin punctele codomeniului

taie graficul în cel puțin un punct

adică ecuația f de x egal cu y

are cel puțin o soluție atunci

funcția este surjectivă Haideți

să vedem în exemplu se cere să

studiem surjectivitatea funcție

de mai jos folosind metoda grafică

avem f definită pe r cu valori

in r f de x egal cu 2x minus 1

dacă x este mai mic decât 0 și

minus x plus 3 Dacă x este mai

mare sau egal cu 0 am reprezentat

grafic această funcție mai întâi

vom face un tabel de valori avem

x de la minus infinit la plus infinit

la stânga lui 0 funcția va avea

valoarea 2 ori 0 minus unu adică

minus unu să mai alegem și eu altă

valoare mai mică decât 0 de exemplu

minus 1 2 ori minus 1 este minus

2 minus 1 minus 3 la dreapta lui

0 funcția va fi 3 și să mai alegem

o altă valoare pentru x mai mare

ca 0 de exemplu 1 minus 1 plus

3 va fi Toy să le prezentăm într

un sistem de axe aceste puncte

pentru x egal cu 0 y este minus

unu pentru x egal cu minus 1 este

minus 3 să ducem o semidreaptă

care trece prin aceste puncte funcția

f de x egal cu 2x minus 1 este

o funcție crescătoare punctul de

coordonate 0 minus 1 nu aparține

graficului funcției Deci avem o

semidreaptă deschisă apoi avem

punctul de coordonate 0 3 Iată

și punctul de coordonate 1 2 funcția

minus x plus 3 este descrescătoare

iar punctul de coordonate 0 3 aparține

graficului prin urmare această

semidreaptă este închisă acesta

este graficul funcției și acum

trebuie să verificăm dacă orice

paralelă la axa o x dusă prin cu

domeniul intersectează graficul

funcției în cel puțin un punct

dacă ducem această paralelă prin

această zonă observăm că ea intersectează

graficul funcției însă dacă ducem

paralela la axa o x prin zona aceasta

Deci pentru yg3 atunci nu avem

punct de intersecție între această

dreaptă și graficul funcției Așadar

pentru luni valori mai mari ca

3 funcția nu este surjectivă în

concluzie funcția f nu este surjectivă