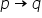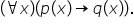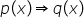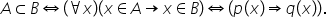Implicația propozițiilor și a predicatelor. Incluziunea mulțimilor

mănânc ce aceasta o să discutăm

despre implicația propozițiilor

și a predicatelor și o să vedem

ce legătură există între implicație

și incluziunea mulțimilor Fiind

date două propoziții pe și q Haideți

să facem tabelul de Valori pentru

propoziția non P sau Q am scris

pe primele două coloane valoarea

de adevăr pentru propozitiile p

și q și acum să scriem valoarea

de adevăr pentru propoziția non

p dacă p este falsă nuntă este

adevărată iar dacă tu este adevărată

nuntă este falsă acum Să completăm

valoarea de adevăr pentru propoziția

non P sau Q ori amintesc că disjuncția

a două propoziții este adevărată

dacă cel puțin una din cele două

propoziții este adevărată Deci

ne uităm pe aceste două coloane

avem cel puțin o propoziție adevărată

prin urmare disjuncția este adevărată

la fel și aici această propoziție

non P sau Q se mai numește și implicația

propozițiilor p și q și se notează

astfel prin urmare acesta este

tabelul de Valori pentru implicația

două propoziții Observați că implicația

este falsă numai atunci când propoziția

apei este adevărată și q este falsă

implicația este o relație de succesiune

logică între două propoziții și

contează ordinea în care sunt scrise

acestea prima propoziție pe se

numește ipoteză iar q se numește

concluzie această implicație se

mai citește și astfel dacă pe atunci

q sau din P rezultă q pe implică

q p este o condiție suficientă

pentru q sau q este o condiție

necesară pentru păr implicația

poate fi privită și ca un raționament

logic ce are loc între două propoziții

dacă plecând de la o ipoteză falsă

făcând un raționament corect se

poate ajunge la o concluzie corectă

dar plecând de la o ipoteză corectăm

Trebuie să facem un raționament

corect pentru a ajunge la o concluzie

corectă să vedem concret niște

exemple Probabil că vă întrebați

Cum este posibil sau plecând de

la o ipoteză falsă să efectuăm

un raționament corect și să ajungem

la o concluzie corectă Iată un

exemplu dacă plec de la ipoteza

greșită că minus doi este egal

cu 2 și aplicăm un raționament

corect de exemplu ridicăm această

relație la pătrat obținem că 4

este egal cu 4 Deci am plecat de

la o ipoteză falsă Am aplicat un

raționament corect și am ajuns

la o concluzie adevărată este posibil

sau plecând de la o ipoteză falsă

să aplicăm un raționament corect

și să ajungem la o concluzie falsă

De exemplu dacă plecăm de la ideea

că trei este egal cu 2 ceea ce

este fals și scădem din ambii membri

ai relației numărul unu obținem

că doi este egal cu unu deci am

ajuns la o concluzie falsă ultimul

caz este cel mai des întâlnit cel

în care plecăm de la o ipoteză

adevărată efectuăm un raționament

corect și ajungem la o concluzie

adevărată de exemplu Dacă 5 este

egal cu 5 și înmulțim această egalitate

cu 2 obținem 10 egal cu 10 am plecat

de la o ipoteză adevărată Am efectuat

un raționament corect și am ajuns

la o concluzie adevărată este interesant

de studiat acest caz în care plecând

de la o ipoteză adevărată putem

ajunge la o concluzie falsă dacă

e factum un raționament greșit

De exemplu plecăm de la ideea de

trei ori zero este egal cu 2 ori

0 pentru că 0 este egal cu zero

prin urmare aici avem o relație

adevărată și afunda Prefect un

raționament greșit De exemplu dacă

împărțim această relație cu 0 obținem

că 3 este egal cu 2dc am ajuns

la o concluzie falsă făcând acest

raționament greșit De fapt acesta

este și motivul pentru care împărțirea

la 0 este o operație fără sens

pentru că Iată Dacă împărțim la

aceasta egalitate la zero ajunge

la o concluzie falsă așa dar atunci

când trebuie să demonstrăm teoremei

în matematică sau diferite relații

trebuie să avem grijă că atunci

când plecăm de la o ipoteză adevărată

să efectuăm un raționament corect

pentru a ajunge la o concluzie

adevărată și atunci să reținem

că implicația a doua propoziție

este falsă numai În condiția încă

rap este adevărată și q este falsă

în toate celelalte situații implicația

este adevărată și acum să vedem

niște exemple avem următoarele

propoziții Dacă 1 plus 1 este egal

cu 5 atunci elefantul zboară știu

că pentru vorbirea curentă această

exprimare nu are niciun sens însă

din punct de vedere matematică

este propoziție cât se poate de

adevărată pentru că Iată 1 plus

1 egal 5 este o ipoteză falsă elefantul

Zboară este o concluzie falsă prin

urmare suntem în prima situație

în care ipoteza și concluzia sunt

false dar implicația este adevărată

Deci iată că noi matematicienii

putem accepta expresii bizare și

mai mult chiar le Considerăm adevărate

următoarea propoziție dacă 2 este

egal cu 3 atunci 5 la 2016 este

egal cu 185 de milioane trei sute

doisprezece mii 755 2 este egal

cu 3 este o ipoteza falsă prin

urmare implicația va fi adevărată

nici nu ne interesează ce valoare

de adevăr are această concluzie

pentru că atâta timp cât ipoteza

este falsă implicația va fi adevărată

prin urmare nu este necesar se

fac Toma cest calcul și ultimul

exemplu dacă 3 plus 7 este egal

cu 10 atunci cinci este mai mic

decât doi avem o ipoteză adevărată

o concluzie falsă prin urmare suntem

în această situație în care implicația

este falsă în continuare o să discutăm

despre implicația predicatelor

Fiind date două predicate pe de

x și q de x spunem că predicatul

pe implică logic predicatul q sau

predicatul q este o consecință

logică a predicatului p dacă propoziția

oricare ar fi x pdx implică q de

x este o propoziție adevărată implicația

predicatelor se notează astfel

de ceartă că la predicate folosim

o săgeată dublă să luăm un exemplu

avem predicatul p de x x mai mic

sau egal decât 3 unde x este număr

natural predicatul q x mai mic

decât 6 unde x se număr natural

și Haideți să vedem dacă are loc

această implicație pdx implică

logic qdx trebuie să verificăm

dacă această propoziție este adevărată

oricare ar fi x în cazul în care

ipoteza este falsă Deci x este

mai mare strict decât 3 atunci

implicația este adevărată am văzut

mai devreme că o implicație cu

ipoteza falsă este adevărată acum

dacă ipoteza ar fi adevărată Deci

x este mai mic sau egal decât 3

trebuie să vedem ce valoare de

adevăr are concluzia și să luăm

un exemplu dacă x este 2 atunci

2 este mai mic decât șase prin

urmare oricare ar fi x mai mic

sau egal decât 3 x este mai mic

decât 6 Deci avem o concluzie adevărată

prin urmare implicația este o propoziție

adevărată să verificăm acum dacă

are loc și implicația inversă dorim

să verificăm dacă predicatul q

implica logic predicatul pe mai

exact trebuie să vedem dacă această

propoziție este adevărată oricare

ar fi x în cazul în care această

ipoteză și falsă Deci sa fie mai

mare sau egal decât 6 atunci automat

implicația este adevărată să vedem

ce se întâmplă dacă ipoteza este

adevărată dacă x este mai mic decât

6 să luăm un exemplu dacă x este

egal cu 5 atunci x este mai mic

sau egal decât 3 răspunsul este

negativ prin urmare această concluzie

nu este adevărată pentru orice

x în cazul în care x este egal

cu 5 această concluzie este falsă

Prin urmare avem o implicație cu

ipoteza adevărată și concluzia

falsă și atunci această implicație

este falsă din moment ce această

propoziție nu este adevărată pentru

orice x înseamnă că această implicație

dintre cele două predicate nu are

loc Cum se scrie mulțimea de adevăr

pentru predicatul te mulțimea de

adevăr a predicatului p de x este

formată din acele numere naturale

mai mici sau egale cu 3 0 1 2 și

3 ce să notăm această mulțime cu

ei mulțimea de adevăr a predicatului

q de x este formată din numerele

naturale mai mici strict decât

6 0 1 2 3 4 și 5 și notăm această

mulțime cu b revenind acum la această

implicație am văzut că dacă x este

mai mic sau egal decât 3 atunci

implicit x este și mai mic decât

6 prin urmare dacă x este un element

din mulțimea A atunci x este și

element din mulțimea b cu alte

cuvinte spunem că mulțimea A este

inclusă în mulțimea B această relație

de incluziune dintre cele două

mulțimi se poate reprezenta printr

o diagramă astfel de spunem că

a este inclusă în mulțimea b dacă

oricare ar fi x un element al mulțimii

A atunci x este și element al mulțimii

b prin urmare să reținem că predicatul

pe implică logic predicatul q Dacă

mulțimea de adevăr a predicatului

p este inclusă în mulțimea de adevăr

a predicatului q în cazul în care

mulțimea de adevăr a predicatului

q nu este inclusă în mulțimea de

adevăr a predicatului p atunci

spunem că predicatul q nu implică

logic predicatul pe se poate observa

Așadar că mulțimea B nu este inclusă

în mulțimea A să mai facem în continuare

un exemplu avem aceste două predicate

predicatul p de x x este mai mare

ca 0 X FI număr real și predicatul

q x pătrat mai mare decât 0 unde

x se numără ne propunem să verificăm

Care dintre aceste două implicații

are loc mai întâi să verificăm

prima implicație trebuie să verificăm

dacă x este mai mare decât 0 atunci

și x pătrat este mai mare decât

0 răspunsul este afirmativ pentru

că pătratul oricărui număr pozitiv

este un număr pozitiv această implicație

este adevărată acum să verificăm

dacă are loc implicația inversă

q de x implică logic pdx mai exact

trebuie să verificăm dacă x pătrat

este mai mare decât 0 atunci și

x este mai mare decât 0 să luăm

un exemplu dacă x este egal cu

minus 2 atunci propoziția q de

minus 2 se scrie astfel minus 2

la pătrat este mai mare decât zero

și Aceasta este o propoziție adevărată

acum să scrie în propoziția pe

de minus 2 minus 2 mai mare ca

0 observăm că aceasta este o propozitie

falsă Deci propoziția oricare ar

fi x din r qdx implică pdx este

o propoziție falsă așa dar această

implicație nu are loc