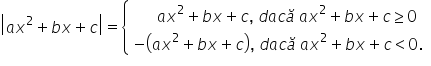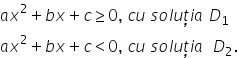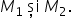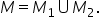Inecuații de gradul II cu modul

în această lecție vom face inecuații

de gradul al doilea ce conțin moduri

pentru început explicitarea modulului

se exprima astfel modul de a este

egal cu A dacă A este mai mare

sau egal ca 0 Deci un număr pozitiv

sau minus a dacă era mai mic decât

0 practic un număr negativ a este

un număr real astfel valoarea oricărui

număr real în modul este pozitiv

de exemplu modul de minus 3 este

egal cu Teo are si vino spre este

negativ și conform explicită rii

practica aceasta a doua ramură

minus 3 va fi egal cu minus minus

3 Deci minus au nostru care este

minus trei și atunci minus cu minus

titlu pentru care corect afirmat

modul de minus trei este trei în

altă ordine modul de 3 egal cu

3 deoarece 3 este pozitiv la conform

explicită recent pe prima ramură

și atunci este chiar număr atunci

când facem referire la inecuații

de gradul al doilea ce conțin modul

este necesar să remarcăm Forma

generală a acestora practic modul

de ax pătrat plus b plus c este

mai mic decât d mai mare decât

a mai mic sau egal decât y mai

mare sau egal decât în condițiile

în care a b c sunt reale ale obligatoriu

diferite seara ca să rămânem pe

gradul al doilea iar Dan poate

să fie real Adică poate să fie

un număr sau de poate să fie expresia

matematică Ce conține variabila

x în această situație explicitarea

modulului se face astfel modul

de a expirat plus bx plus c este

egal cu ax pătrat plus pe x plus

c dacă ai pătrat pe expuse mai

mare sau egal ca 0 respectiv minus

ax pătrat plus bx plus c dacă a

x pătrat plus pe explici ce este

mai mic decât să Observați în cazul

1 respectiv cazul 2 Acestea fiind

condițiile în care modulul ia această

valoare sau această valoare sunt

de fapt inecuații de gradul al

doilea inecuații pe care am învățat

să le rezolvăm între o lecție precedent

pentru explicitarea corectă a modulului

este necesară rezolvarea inecuațiilor

ce se constituie drept condiții

rezolvarea acestora conduce la

domeniul pe care x Ulpia valori

pentru fiecare din cele două situații

exprimati txm modul de x pătrat

plus 3x plus c este egal cu x pătrat

plus bx plus c dacă x aparține

minus infinit X1 reunit cu x 2

plus infinit Asta înseamnă în afara

rădăcinilor și pe a doua situație

ax pătrat minus pe x plus si daca

x aparține lui x 1 x 2 Observați

între rătăci sau egal cu doi deci

practic între rădăcini respectiv

minus x pătrat minus pe x minus

c dacă x aparține lui minus infinit

X1 reunit cu x 2 plus infinit iar

spun în afara rădăcinilor după

determinarea domeniilor pentru

fiecare dintre cele două situații

se trece la rezolvarea inecuației

inițial Adică două inecuații câte

una pentru fiecare situație adică

pentru prima situație am de rezolvat

ecuații pentru a doua situația

în de rezolvat o inecuații soluțiile

obținute pentru fiecare dintre

cele două inecuații rezolvate sunt

intersectate cu domeniul de discuție

al acestora foarte important intersectat

astfel se obțin mulțimile de soluții

ale inecuațiilor notate cu M1 respectiv

m2 M1 soluția primei inecuații

pe prima situație și m2 soluția

celei de a doua inecuații pe cea

de a doua situație pentru obținerea

soluției finale soluția inecuației

Ce conține modul de soluție a inecuației

date practic se face prin Reuniunea

iar foarte important mulțimilor

M1 și m2 pentru o cât mai bună

înțelegere a celor mai sus comentate

o să dau câteva exemple astfel

exemplu să se rezolve inecuațiile

modul de x pătrat minus 5x plus

6 mai mic decât doi în prima etapă

explicitarea modulului și anume

modul de x pătrat minus 5x plus

6 x pătrat minus 5x plus 6 dacă

x pătrat minus 5x plus 6 este mai

mare sau egal decât 0 respectiv

minus x pătrat minus 5x plus 6

dacă x pătrat minus 5 x 6 este

mai mic decât 0 în aceste condiții

4c se aminti rezolvam ecuația de

gradul al doilea ecuații care nu

acest moment are Delta calculat

1 pozitivi am rătăci reale distincte

rădăcinile în cazul meu calculate

2 respectiv 3 așa cum va duceti

aminte din lecția precedent a egal

cu unu care e pozitiv picioare

plus când Delta este mai mare ca

0 înțeleg De fapt că între rădăcini

am contrar lui a în cazul nostru

minus în afara rădăcinilor avem

semnul lui a astfel în condițiile

date modul de x pătrat minus 6

x pătrat minus 5x plus 6 dacă listează

mai mare sau egal Precizează plus

și atunci în afara rătăci atunci

x pătrat minus 5x plus 6 Cum spunea

dacă x aparține minus Infinit 2

primar reunit cu trei fiind datoare

de cina a doua situație voi avea

minus x pătrat plus cinci x minus

6 dacă x aparține lui 2 3 valul

practic între rădăcini semn contrar

În condițiile în care aici mă interesa

mai mic decât 0 fiecare din aceste

două situații la notat cu steluță

un de spectiv steluță 2 situații

care urmează a fi rezolvat practic

situația 1 pentru x aparține intervalului

minus Infinit 2 de Unite cu 3 plus

in fie a v x pătrat minus 5x plus

6 mai mic decât 2 mai mic decât

doi mașina era inecuația inițial

Deci Vitan rezolvare se trece doi

în partea celaltă cu sens schimbat

aici în partea stângă obținând

astfel x pătrat minus 5x plus patru

ecuația corespunzătoare inecuații

obținute Delta i20 5016 iar pozitii

rădăcini reale și distincte X1

calculat este 5.302 1 x 2 calculați

5 plus 3 supra 2 4 în aceste condiții

am a egal cu unu pozitiv iceam

enterita pozitiv între rădăcini

semn contrar minus în afară de

cine lor genului a plus Pe mine

mă interesează în ecuația nu mai

mic semnul înțeleg că x ul aparține

intervalului 1 4 deschis pentru

că nu am și egal soluția M1 se

obține așa cum spuneam prin intersectarea

Domeniului variabilei x domeniul

acesta și soluția obținută soluția

fiind am1 va fi egal cu minus Infinit

2 reunit cu 3 plus infinit intersectat

cu 1 4 așa cum a fost domeniu respectiv

sunați va fi unu doi da deschis

la 1:00 închis la 2:00 reunit cu

3 4 1 2 3 4 deschis și a doua situație

este discutată în continuare înțelegând

pentru x aparține lui 2 3 4 cea

a doua situație 2 3 intervalul

deschis 2 3 minus x pătrat plus

5x minus 6 mai mic decât doi la

fel minus doi se duce în partea

cealaltă cu Sebi schimbat minus

x pătrat plus 5x minus 6 minus

2 mai mic decât 0 Carrefour musics

pătrat plus 5x minus o înmulțesc

inecuația cu minus 1 și obțin x

pătrat minus 5x plus 8 mai mare

de această dată decât zero va reamintesc

că înmulțirea unei inecuații cu

mine nu presupune schimbarea semnelor

și sensului inegalitate ecuația

corespunzătoare este rezolvată

2532 negativ înțeleg că X1 și X2

nu aparțin numerelor reale Deci

nu avem soluții reale cu cât nu

avem soluții reale vă reamintesc

graficul nu atingea axei o x și

atunci pentru a pozitivi Delta

negativ semnul pe care prezenta

funcția corespunzătoare Nica citate

era plus peste tot Adică pur practic

x aparține mulțimii real în acest

caz soluția in doi se obține prin

intersectarea Domeniului iar spume

în acest caz doi trei și soluția

obținută soluția obținută în acest

caz x aparține lui r astfel m2

va fi 2 3 intersectat cu el în

mod Evident m2 este 2 3 până aici

înțeleg că mo este un doi la un

închis la 2:00 reunit cu 3 4 închis

la 3 deschis la 4 m 2 este 2 3

deschis în ambele capete soluția

finală sau soluția inecuației ce

conține soluția inecuației dat

inițial este m egal cu M1 reunit

de această dată cu doi M1 reunit

cu m2 soluție finală 1 4 un al

doilea exemplu pe care vi propun

este să se rezolve inecuația modul

de x pătrat minus 3x plus 2 mai

mic sau egal decât x plus 7 explicitarea

este x pătrat minus 3x plus 2 dacă

x pătrat minus 3x plus 2 este mai

mare sau egal decât 0 respectiv

x pătrat plus 3x minus 2x pătrat

miniștri pisoi mai mic decât Z

ecuația corespunzătoare Delta 9

minus 8 mai mare decât 0 avem rădăcini

reale și distincte x12 va fi minus

fac plus minus radical din Delta

supra 2-a înțelegând de aici minus

minus trei deci trei plus minus

radical din 1 supra 2-a 2 ori 1

adică 2 astfel X1 va fi 3 minus

1 supra 2 adică doi pe doi unu

respectiv x23 Plus supra 2 adică

4 supra 2 în aceste condiții explicitarea

modulului x pătrat minus 3x plus

2 va fi x pătrat minus 3x plus

2 daca x aparține pentru că mă

interesează mai mare bază în afara

rădăcinilor aur fiind pozitiv pozitiv

soluția pentru mai mare sau egal

este în afara rădăcini și atunci

x aparține lui minus infinit reunit

cu 2 plus infinit închis la un

și la 2:00 pentru că avem și egal

respectiv minus x pătrat plus 3

minus 2 dacă x aparține în interiorul

rădăcinilor în cazul meu 1 2 deschis

întrucât avem strict mai mic astfel

prima situație comentată va fi

cea în care x aparține intervalului

minus infinit 1 cu doi pasi fii

în aceste condiții inecuația noastră

devine x pătrat minus 3x plus 2

situația aceasta mai mic sau egal

decât x plus 7 se trec toți termenii

în partea stângă cu sens schimbat

astfel x pătrat minus 3x plus 2

minus x minus 7 mai mic sau egal

decât 0 rezolvăm evident și atunci

avem x pătrat minus 4x minus 5

mai mic sau egal decât cel ecuația

corespunzătoare x pătrat minus

4 x 5 egal cu 0 Delta va fi 16

plus 20 adică 36 iar pozitivi rădăcini

reale și distincte x12 va fi minus

b Deci 4 plus minus radical din

Delta de 6 supra 2-a 2 înțeleg

de aici că X1 va fi 4 minus 6 minus

2 Deci 1 x 2 fac fie patru plus

șase zece supra 2 5 pentru că mă

interesează mai mic sau egal înțeleg

că mă interesează semn contrar

lui a se în contra lui a întrerupe

și în condițiile în care auri este

1 și pozitiv astfel x aparține

intervalului minus unu Deci M1

este minus infinit 1 reunit cu

2 plus infinit intersectat cu minus

unu cinci unu respectiv 5 m în

aceste condiții va fi minus 1 reunit

cu 2 și 5 cea de a doua situație

pentru x aparține intervalului

1 2 deschis la om deschisa 2 ab

minus x plus 3 minus 2 mai mic

sau egal decât x plus 7 ce trec

toți termenii partea stângă Evident

cu sens schimbat obținând astfel

minus x pătrat plus 3x minus 2

minus x minus 7 mai mic sau egal

decât rezolvăm minus x pătrat 3x

minus x 2x minus 2 minus 7 minus

9 mai mic sau egal decât 0 înmulțesc

inecuația cu minus 1 obțină inecuația

x pătrat minus 2x plus 9 mai mare

sau egal cu 0 ecuația corespunzătoare

x pătrat minus 2x plus 9 egal cu

0 Delta egal cu 4 minus 36 negativ

înțeleg încă X1 X2 nu aparțin lui

R pentru că aul este pozitiv Da

se află deasupra axei Da și întotdeauna

va fi pozitiv în condițiile astea

x aparține lui r este soluția aceste

inecuații astfel 1 2 vă reamintesc

era domeniu el era soluție în aceste

condiții m2 va fi unu doi Deci

soluția inecuației date este m

egal cu 1 reunit cu m 2 m este

minus unu unu reunit cu 2 5 acesta

fiind m1da reunit cu 1 2 acesta

fiind m2 în aceste condiții soluția

inecuației tate va Fie m egal cu

minus unu până la cinci unu doi

a completat si lipsa din acest

interval