Înmulțirea matricelor

Să presupunem că ești managerul

unei firme care comercializează

produse de patiserie și vrei să

știi care sunt sumele încasate

în ultimele patru zile produsele

comercializate sunt afișate în

această lume atrice l iar cantitățile

comercializate sunt cuprinse în

acest tabel matricea Cum vei proceda

dacă vei dori să știi care este

valoarea vânzărilor din ziua de

luni vei calcula cazările pentru

plăcinta cu carne Înmulțind prețul

unei plăcinte cu numărul de bucăți

vândute 6 înmulțit cu 40 pentru

plăcinta cu pui Înmulțind pe 4

cu 50 pentru plăcinta cu legume

3 înmulțit cu 82 și pentru tortul

cu ciocolată 5 înmulțit cu 89 însumând

aceste produse obținem suma totală

încasată în ziua de luni adică

1131 RON pe procedat la fel și

pentru celelalte zile adică de

calcul la produsul 6 înmulțit cu

8 53 4 înmulțit cu 43 3 înmulțit

cu 90 5 înmulțit cu 99 însumând

aceste produse obținem suma încasată

pentru ziua de marți adică 1255

înmulțim apoi 6 cu 84 cu 103 150

5 cu 100 însumând acum aceste produse

obținem suma încasată în ziua de

miercuri și anume 1830 înmulțim

acum pe 6 45 pe 4 cu 60 pe 385

și pe 5 cu 109 însumând aceste

produse obținem suma încasată pentru

ziua de joi și anume 1310 tabelului

metal care conține prețurile produselor

îi corespunde matricea a de tipul

1 ori 4 tabelului matriceal care

conține cantitățile vândute îi

corespunde matricea b de tipul

patru ori patru iar sumelor încasate

în fiecare din cele patru zile

îi corespunde matricea si de tipul

1 ori 4 putem spune că matricea

Ce este produsul matricelor a orbi

amintind un modul în care Am calculat

elementele matricei Ce observăm

că este necesar ca numărul de coloane

ale matricei a să fie egal cu numărul

de linii al matricei b iar matricea

ce are numărul de linii egal cu

numărul de linii al patriciei a

iar numărul de coloane egal cu

cel al matricei b să definim acum

Produsul a două Matrice Fie a o

matrice de tipul MN cu n elemente

în mulțimea numerelor complexe

a și b Matrice de mp cu elemente

în mulțimea numerelor complexe

numim produsul matricelor a și

b matricea de tipul mp cu elemente

în c ale cărei elemente se calculează

astfel elementul cheie j este suma

produselor elementelor liniei II

din matricea a cu elementele coloanei

j din matricea de altfel spus elementele

liniei e din matricea a se înmulțesc

cu elementele coloanei din matricea

b obținând un se elementul cheie

adică cel care corespunde liniei

și coloanei j din matricea produs

iar elementul ce i se calculează

a 1-a mulți tcu B1 j plus a e 2

înmulțit cu D2 j plus a.in înmulțit

cu B n j produsul matricelor și

b notăm cu a ori b sau a b iar

operația prin care asociem unei

perechi de Matrice a b în condițiile

de mai sus matricea a or b se numește

înmulțirea matricelor să calculăm

acum produsul matricelor a egal

cu 1 2 minus 2 0 4 minus 1 Matrice

de tipul 3 2 cu elemente în sat

ca matricea b egală cu minus 1

4 0 3 minus 2 minus 3 Matrice de

tipul 2 3 cu elemente din z adică

viman mulți liniile matricei a

cu coloanele matricei b procedăm

la fel și cu linia a doua elementele

matricei a ori b le obținem astfel

1 ori minus 1 plus 2 ori 3 1 ori

plus 2 ori minus doi unu 0 plus

2 ori minus 3 procedăm la fel cu

linia a doua minus 2 ori minus

1 plus 0 ori 3 minus 2 ori 4 plus

0 minus 2 plus 0 ori minus trei

la fel cu linia a treia patru ori

minus 1 plus minus 1 ori 3 4 ori

4 plus minus 1 ori minus 2 4 ori

0 plus minus 1 ori minus 3 obținem

astfel rezultatele minus 1 plus

6 4 minus 4 0 minus 6 2 plus 0

minus 8 plus zero zero plus 0 minus

4 minus 316 plus 2 0 plus 3 adică

matricea 5 0 minus 6 2 minus 8

0 minus 718 3 Adică o matrice de

tipul 33 cu elemente în mulțimea

numerelor întregi
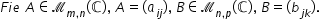
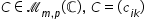
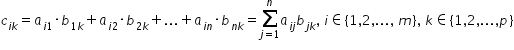