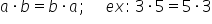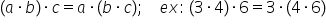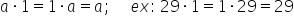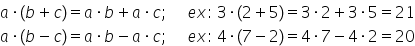Înmulțirea numerelor naturale
Tag-uri
Partajeaza in Google Classroom

Transcript
în continuare o să discutăm despre
înmulțirea numerelor naturale ce
avem aici un exemplu 3 ori 5 din
cu toții egal 15 operația de înmulțire
este reprezentată prin acest punct
și acum Haideți să ne amintim Cum
se numesc numerele care fac parte
dintre o înmulțire cele două numere
cazul nostru Avem două care se
înmulțesc poartă numele de factori
Deci notăm aici factori în schimb
si rezultatul Care este 15 aici
poartă numele de produs Deci când
avem de a face cu înmulțire numerele
care se înmulțesc se numesc factori
iar rezultatul se numește produs
de fapt ce este înmulțirea înmulțirea
este o adunare repetată cu alte
cuvinte 3 înmulțit cu Haide să
notăm Deci avem așa 3 înmulțit
cu 5 este egal cu Ce înseamnă înseamnă
că avem de trei ori câte cinci
Deci venim aici notăm 5 plus 5
plus 5 și rezultatul este 5 cu
5 10 cu 515 Haideți să scriem tot
cu alb Rezultatul este 15 bun acum
știm deja înmulțire o adunare repetată
să facem și câteva exerciții de
exemplu să înmulțim pe 23 cu 10
Ce se întâmplă când înmulțim numere
cu 10 100 1000 și așa mai departe
Păi scriem numărul respectiv 23
2 3 și adăugăm la final un zero
pentru că la 10:00 avem o singură
cifră de 0 2 și rezultatul este
230 dacă aveam însă templu 158
înmulțit acum cu 1000 ce obținea
Păi trecem cifrele pe care le avem
aici Adică 1 5 8 la care mai adăugăm
Iată 1 2 3 de 0 și rezultatul este
158.000 alt exemplu dacă avem de
a face cu astfel de înmulțire 12
înmulțit cu 400 Păi în asemenea
situații putem să ne gândim în
felul următor Avem 12 înmulțit
cu pe 400 putem scrie 4 înmulțit
cu 100 de fapt putem să facem mai
întâi acest produs 12 ori 4 direct
48 și mai adăugăm c20 week avem
aici ori 100 Deci răspunsul este
4.800 Haideți acum să facem următoarea
înmulțire Să considerăm că avem
o 29 Deci 129 pe care îl înmulțim
cu 15 bun când avem asemenea înmulțirii
cel mai bine este să trecem numerele
unele sub altele astfel încât cum
le așezăm Păi trebuie să avem unitățile
subunități zecile 10 așa mai departe
Și începem și înmulțim îl vom înmulții
pe 5 cu 129 apoi pe unul îl înmulțim
cu 129 5 ori 9 ne dă 45 Deci scriem
cinci și patru în minte Uite am
trecut cu roșu ce ținem în minte
cinci ore 2 ne dă 10 cu 4 din minte
14 Deci trece în patru și trecem
unul minte cinci ori 1 5 cu unul
din minte 6 deci venim aici și
satul și calcul momentan e 645
acum pe unul îl înmulțim cu 9 1
ori nouă ne dă nouă dar unde trecem
pe 9 Păi Vandici în aceeași coloană
cu unul de aici avem nouă unu ori
doi doi unu unu unu și acum adunăm
ce am obținut avem aici cinci patru
cu nouă ne dă 13 Deci avem trei
și unu în minte șase cu doi opt
cu unul din minte 961 Deci avem
1935 un alt exemplu să calculăm
acum 1003 haide să scrie mai jos
Deci avem 1003 înmulțit cu 24 Deci
scriem numerele unele sub altele
Și începem înmulțirea 4 ori 3 ne
dă 12 Deci trecem 2 și 1 în minte
4 ori 0 zero cu unul din minte
ne dă 1 4 ori 0 0 12 mai si 0 și
4 ori 1 ne dă 4 2 ori 3 ne dă 6
unde îl trecem pe 6 în dreptul
în aceeași coloană cu doi Deci
aici 2 ori zero zero deja știți
doar încă un zero zero și Avem
doi ori unu adică 2 Și acum în
sumă Avem doi unul cu șase ne dă
7 aici obținem 0 aici avem patru
și îl coborâm pe 2 Rezultatul este
24.000 72 în aceste calcule am
folosit faptul că 4 ori 0 ne dă
0 2 ori 0 ne dă tot așa 0 de fapt
aici putem nota observație pe care
sigur si mai mult te voi deja o
știți orice număr natural să îl
numim a înmulțit cu 0 o să ne dea
întotdeauna 0 Deci dacă înmulțim
cu 0 orice număr natural rezultatul
pe care îl obținem este 0 acum
la începutul discuției noastre
am spus că înmulțirea este de faptul
are repetată și am avut acest exemplu
3 ori 5 îl putem citi de trei ori
câte cinci și avem aici 5 plus
5 plus 5 egal 15 dacă însă avem
acest calcul 5 înmulțit cu 3 Cum
îl putem citi Păi avem de 5 ori
câte trei Deci 3 plus 3 De câte
ori scrie mă scriem pe 3 de cinci
ori și rezultatul va fi trei cu
trei șase cu trei nouă cu 312 cu
315 bun de fapt ce observam iată
că 3 înmulțit cu 5 Deci 3 ori 5
este 1 6 lași lucru cu 5 în Fit
cu trei unde am mai văzut noi această
schimbare de poziție a numerelor
am văzut la operația de adunare
3 plus 5 acea lucru cu 5 plus 3
de fapt vorbim aici de proprietățile
înmulțirii și prima proprietate
este cea care se numește ca și
la adunare comutativitate Ce înseamnă
comutativitatea de fapt că dacă
avem două numere naturale să le
spunem a și b produsul lor a orbi
același lucru cu b înmulțit cu
ei cea de a doua proprietate Haideți
să vedem dacă și înmulțirea este
ca și adunarea o operație asociativă
și facem acest calcul să vedem
dacă 3 ori 4 totul înmulțit cu
șase o fi Oare același lucru cu
3 înmulțit cu acest produs 4 ori
6 pe facem calculul aici cât avem
12 ori 6 care ne dă 72 și în această
parte ce obținem Păi îl păstrăm
pe 3 4 ori 624 trei ori 24 înseamnă
72 apoi de fapt avem egalitate
asta înseamnă că putem să ștergem
cu încrederea acest semn de întrebare
alte cuvinte aici 3 ori 4 totul
înmulțit cu 6 egal cu 3 ori acest
produs patru ori 6 cu alte cuvinte
scriem proprietatea de asociativitate
Deci dacă avem să notăm și aici
a b și c trei numere naturale putem
să calculăm produsul lor astfel
mai întâi îl înmulțim pe a cu b
și apoi rezultatul cu c sau pe
ei îl înmulțim cu rezultatul produsului
b ori c mult Haide să discutăm
în continuare de încă o proprietate
Deci notăm proprietatea numărul
3 Care E una foarte simplă Ce număr
înmulțit de exemplu cu 29 ne dă
tot 29 Păi înseamnă că aici avem
numărul unu Deci în loc de semn
de întrebare scriem 1 de fapt 1
este elementul neutru al operației
de înmulțire pentru că unu nu schimbă
cu nimic produsul rezultatul unui
produs față de adunare mai discutăm
aici de încă o proprietate și anume
înmulțirea este distributivă față
de adunare și scădere Deci trecem
aici proprietatea numărul 4 acum
Ce înseamnă că este distribuția
fă față de adunare și față de scădere
pe să facem următorul exemplu 3
înmulțit cu doi plus cinci și să
facem acest calcul Păi avem de
fapt 3 înmulțit cu facem mai întâi
calcul din paranteză ori 7 ne dă
21 dar dacă calculăm 3 ori 2 adunat
cu 3 ori 5 cât obținem Păi avem
aici 6 avem ai 15 Deci obținem
tot 21 Păi de fapt Ce rezultă rezultă
că 3 înmulțit cu acest calcul din
paranteză e unul și același lucru
cu ce avem în această parte adică
acest acest calcul este egal cu
acesta avem trei ori 2 plus 3 ori
5 E bine Asta înseamnă distributivitatea
față de adunare iar dacă pe trei
îl distribui acest termen însăși
în acest așa avem trei ori 2 și
3 ori 5 Oare acum înmulțirea este
distributivă și față de operația
de scădere de exemplu 4 înmulțit
cu șapte minus doi este egal cu
4 ori 7 minus 4 ori 2 caiete să
vedem facem calculul aici avem
4 înmulțit cu cinci rezultatul
este 20 aici avem 28 minus 4 2
8 rezultatul e tot 20 eclar avem
egalitate deci putem să ștergem
semnul de întrebare cu alte cuvinte
înmulțirea este distributivă și
față de scădere Iată pe patul distribuim
la fiecare termen în parte și avem
patru ore șapte și patru ori doi
acum am tot vorbit despre Pro pietății
să las le folosim și vă voi da
un câteva exemple legate de primele
două proprietăți de comutativitate
și asociativitate mai întâi aceste
două proprietăți ne sunt de mare
ajutor atunci când vrem să calculăm
rapid de exemplu dacă avem cinci
ori optisprezece înmulțit cu doi
Păi nu Ce să facem cinci ore 18
și apoi să înmulțim cu 2 nu e mai
simplu să înmulțim direct pe 5
cu doi Ba da putem să facem acest
lucru Păi pentru a face așa trebuie
să aplicăm Ce proprietate Păi aplică
mai întâi aici proprietatea de
comutativitate scriu aici Cum de
la comutativitate și schimbăm locul
acestor doi factori și avem 18
ori 5 ori 2 De ce facem acest lucru
pentru că această scriere ne permite
să folosim acum asocia invitat
ea și îl înmulțim mai întâi pe
5 cu doi de c egal mai departe
cu 18 adică 180 iată că putem face
calcul foarte rapid chiar și în
minte exemplu 2 înmulțit cu 43
înmulțit cu 15 la fel ce face aplicăm
aici comutativitatea și vom avea
așa 2 înmulțit cu Deci 2 înmulțit
cu 15 înmulțit cu 43 de ce folosim
această scriere Păi putem să facem
2 ori 15 care ne dă mai departe
30 ori 43 Cum îl scriem pe 30 pe
avem 10 ori trei ori 43 facem acum
acest calcul care ușor de văzut
că ne dă 129 Deci notăm egal mai
departe cu 129 ca orz de ce Deci
mai adăugăm un zero Deci rezultatul
e 1290 aici vom dat explicațiile
detalii ei dar sigur făcând Aplicând
comutativitatea și asociativitatea
Puteți să faceți calculul direct
în minte despre utilitatea acestei
proprietăți a faptului că înmulțirea
este distributivă față de adunare
și scădere vom discuta între o
altă secvență

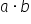 . Numerele a și b se numesc factori, iar rezultatul înmulțirii se numește produs.
. Numerele a și b se numesc factori, iar rezultatul înmulțirii se numește produs.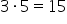 ; 3 și 5 se numesc factori, iar 15 se numește produs.
; 3 și 5 se numesc factori, iar 15 se numește produs.