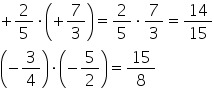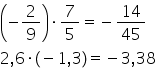Înmulțirea numerelor raționale
Tag-uri
Partajeaza in Google Classroom
Transcript
pentru Înmulțirea și împărțirea
numerelor raționale avem aceleași
reguli ale semnelor ca și la operațiile
cu numere întregi și anume produsul
a două numere raționale cu semne
diferite este negativ iar valoarea
absolută a produsului este egală
cu produsul valorilor absolute
ale factorilor produsul a două
numere raționale cu același semn
este pozitiv iar valoarea absolută
a produsului este egală cu produsul
valorilor absolute ale factorilor
pe scurt Dacă vom înmulțiri două
fracții cu același semn și el pozitiv
sau negativ rezultatul va fi întotdeauna
pozitiv Hei dacă înmulțim două
fracții având semne diferite rezultatul
va fi întotdeauna un număr negativ
plus 1 supra 5 ori plus doi supra
trei plus ori plus este Plus și
acum înmulțim fracțiile așa cum
știm deja și anume se înmulțesc
numărătorii 3 și numitorii între
a 1 ori 2 supra 5 ori 3 are va
fi egal cu plus 2 supra 15 putem
să nu mai scriem Semnul plus în
cazul numerelor pozitive Și atunci
vom scrie egal cu 2 supra 15 al
doilea exercițiu minus 2 supra
5 ori minus 3 supra 7 stabilim
întâi sternul rezultatului minus
ori minus este Plus la numărător
avem 2 ori 3 supra 5 ori 7 care
va fi egal cu 6 supra 35 al treilea
exercițiu minus 6 supra 5 ori plus
1 supra 8 minus ori plus este minus
6 ori 1 supra 5 ori 8 egal mai
departe cu minus 6 supra 40 această
fracție se mai simplifică cu 2
și obținem minus 3 supra 20 al
patrulea exercițiu minus 1 supra
9 ori plus 3 supra 7 Ne uităm dacă
nu putem să simplificăm pe diagonală
observăm că 9 este un multiplu
al numărului 3 și atunci putem
să simplificăm cu 3 9 împărțit
la 3 la fie 3 iar 3 împărțit la
3 este 1 minus ori plus este minus
la numărător avem 1 ori 1 care
este 1 iar la numitor avem trei
ori 721 5 minus 5 ori minus 2 supra
10 putem să simplificăm pe diagonală
cu 5 5 împărțit la 5 este 1 iar
10 împărțit la 5 este 2 minus ori
minus este Plus 1 ori 2 este 2
supra 2 iar 2 supra 2 este egal
cu 1 6 minus 2 supra 3 ori 5 supra
7 ori minus 3 supra 4 minus ori
plus este minus Deci Rezultatul
înmulțirii primelor două fracții
este negativ apoi Înmulțind un
număr negativ cu un alt număr negativ
se obține un număr pozitiv zici
semnul rezultatului final va fi
plus înmulțim toți numărătorii
între ei și numitorii între ei
2 ori 5 ori 3 supra 3 ori 7 ori
4 putem să simplificăm cu trei
de oarece apare atât la numitor
cât și la numărător 3 împărțit
la 3 este 1 putem să mai simplificăm
și cu 2 2 împărțit la 2 este 1
și 4 pățit la 2 este 2 la numărător
obținem 1 ori 5 ori 1 care este
egal cu 5 iar la numitor avem unul
7 ori 2 care este egal cu 14 puteam
să simplificăm chiar de la început
pe diagonală cu 3 și pe cealaltă
diagonală cu 2
Înmulțirea numerelor raționaleAscunde teorie X
Navigare în lectii
Cumpara abonament
