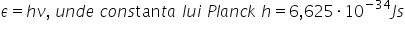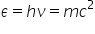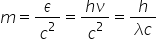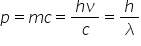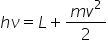Ipoteza Planck. Fotonul. Explicarea efectului fotoelectric cu modelul corpuscular.

în cea de a doua lecții de fizică

cuantică vom discuta despre ipoteza

planck despre Foton și despre formula

asta în lecția trecută am prezentat

efectul fotoelectric extern Și

am discutat spre sfârșitul lecției

despre faptul că modelul ondulatorul

al luminii nu reușește să explice

niciuna din legile stabilite experimental

pentru acest experiment vom discuta

în această Lecție despre soluția

în soluția care explică acel experiment

și anume fizica cuantică sau interpretarea

cuantică a luminii și a radiației

electromagnetice În ce an era această

pleacă de la așa numita ipoteză

plank a cuantelor de energie plank

tot în jurul anului 1900 a speculat

pe baza unor anumite rezultate

experimentale că o și laturii electromagnetici

microscopici adică atomi și electroni

din materialele ce ne înconjoară

emit și absoarbe energie în cantități

discrete care se numesc cuante

de energie Ce sunt multiplii întregi

ai unei cantități elementare de

energie pe care o notată cu epsilon

și este egală cu o constantă numită

Constanța planck constant universală

planck H care are aceasta valoare

muncită cu frecvență sau exprimată

în funcție de lungimea de undă

H Constanța planck înmulțită cu

viteza luminii în vid împărțită

la lungimea de unt Ce înseamnă

această ipoteză înseamnă că atomi

și electroni Deci particule microscopice

din materia care ne înconjoară

se comportă un mod foarte straniu

pentru fenomenele fizice cunoscute

la vremea respectivă și anume energia

lor e nu ia valori continui si

ia valori discrete sau cuantificate

sunt multiplii de sunt energia

este egală cu un număr n înmulțită

cu acest epsilon Deci energia unui

electron în atom sau în general

energia la acest nivel particulelor

și sistemelor fizice la acest nivel

microscopic ia valori epsilon 2

epsilon 3 epsilon și așa mai departe

și niciodată valorile între epsilon

și 2 epsilon aceasta era o idee

foarte îndrăzneață la vremea respectivă

pentru că nu se auzise în fizică

de așa ceva toate procesele cunoscute

din mecanică din electro magnetista

vremea respectivă avea o distribuție

continuă a energiei și Deci această

ipoteză el a lui planck și ecuația

asociată a pentru cuanta de energie

a rămas ca să spunem așa în dormitoare

pentru câțiva ani până când ia

fost aplicată pentru explicarea

cu succes a Experimentelor de tip

efect fotoelectric sau efect canta

Haideți să continuăm să vedem cum

În primul rând după cum am spus

nu în acea ecuații este frecvența

oscilatorului microscopică atomului

sau electronului care emite radiații

electromagnetică prin oscilația

sun și să spunem că plec la momentul

emiterii acestei ideea Ce este

ipoteze nu atribuia o existență

reală acestor cuante și niciun

mechanist de formare a lor deci

pur și simplu ce spunea Plant este

că atunci când un atom sau în electron

și în concluzie emite o undă electromagnetică

nu o faci împrumut continuu și

că există un anumit mechanism necunoscut

de origine necunoscută care face

ca energia lui atomului electronului

să varieze în pași în trepte sau

exprimarea corectă științific în

cuante de energie dar el nu atribuiau

existența reală acestor cu Gente

De ce erau pur și simplu mecanici

de variației energiei care se făcea

în trepte sau în cante datorită

unui mecanism necunoscut a trebuit

ca Einstein să vină cu o idee și

mai îndrăzneață decât a lui planck

și anume în Lumina propriei ecuații

ce Stabilește relația masa energie

vă aduc frică sau vă aduc aminte

că Einstein în exact aceeași perioadă

Einstein își construia teoria relativității

despre care am vorbit care conține

faimoasă energie ecuație Einstein

egal cu MC pătrat ce Stabilește

o conexiune directă între energie

și masă în particular masa devenind

o forma de manifestare în particulară

a Energy și Deci Einstein la ipoteza

plantațiile e pentru efectul fotoelectric

a realizat că se poate face un

pas înainte și anume dacă există

o quanta de energie Atunci trebuie

să îi fie asociată o formă de existență

dacă vreți o masa ceea ce ar însemna

că există un sistem fizic care

poartă această cuanta de energie

Adică o particulă de calul al anumitor

Deci fotonul aș fi o existență

reală această rezistență reală

prin care se manifestă cu altele

de energie și care poartă din punct

de vedere energetic aceasta aceste

epsilon în care în radiația electromagnetică

aceasta era un pas înainte în ideea

îndrăzneață a lui planck și cum

prima consecință este că lumina

capătă pe lângă natura ondulatorie

bine stabilită la vremea respectivă

din toate experimental experientele

bine studiate și de către noi de

interferență difracție polarizare

și așa mai departe toate se Explică

pe baza naturii ondulatorii al

luminii sau radiație cromate de

ce lumina capătă salariați electronii

capătă și o natură corpuscular

adică formată din particule radiați

electromagnetică dintre odată se

manifestă în două feluri complet

diferite ca undă și ca particulă

particula fiind bineînțeles fotonul

aceasta era un aceste idei erau

complet noi la vremea respectivă

foarte greu de acceptat pentru

că contraziceau toată cunoașterea

fizicii de până în momentul respectiv

și ele în final au dus la un nou

domeniu al fizicii numit fizica

cuantică Haide să vedem cum aceste

idei erau atât de îndrăzneții încât

ele nu ar fi fost acceptate dacă

experimente clar studiate nu ar

fi susținut în mod practic aceste

idei înainte de a discuta bineînțeles

despre explicarea efectului fotoelectric

pe baza fotonului și a ipotezei

să discutăm despre proprietățile

fotonului il rezultă imediat din

Definiția lui În primul rând fiind

particular ce formează tipul particular

de radiații electromagnetică numită

lumina atunci în vid el trebuie

să aibă viteza egală preciz cu

ce viteza luminii în vid pentru

că fotonul formează lumina este

particula din care lumina sau la

viață cromatică este format Deci

în vid viteza fotonului trebuie

să fie exact ce iar un alt material

oarecare ar trebui să fie C împărțit

la indicele de refracție de aici

rezultă că el trebuie să aibă o

masa de repaus exact egală cu zero

această deoarece după cum știm

masa unei particule din fizica

relativă stă este egală cu 0 împărțit

la radical din 1 minus viteza particula

pătrat împărțită la ce pătrat dar

dacă particula noastră are exact

viteza c rezultă că acest raport

este unul și de ce obținem m 0

împărțit la 0 masă este în 0 împărțit

la 0 masa fotonului un sistem de

referință inerțială oarecare Bineînțeles

că aceasta implică obligatoriu

camasa 0 să fie zero pentru că

numai atunci Numai pentru o masă

îmi 0 egal cu 0 1 obținem o masă

infinită orice valoare diferită

de 0 a lui m0 ar implica un putin

cu masa de mișcare infinit ceea

ce este inacceptabil din punct

de vedere fizic rezultă obligatoriu

m0 trebuie să fie zero și atunci

și masă în orice un sistem de referință

va fi 0 împărțit la 0 care este

0 energia fotonului trebuie să

respecte atât ecuația nici tine

e egal cu MC pătrat din teoria

relativității restrânse cât și

ecuația planck pentru ecuația plang

spune că energia unei cuante de

energie este hazliu dar cuanta

de energie pentru radiați electromagnetică

este fotonul de sinergie a fotonului

trebuie să fie egală cu HD Deci

pentru energie trebuie energia

fotonului trebuie să respectăm

simultan ambele ecuații de aici

rezultă masa de mișcare bineînțeles

aceasta este masa de mișcare nu

de repaus a fotonului care trebuie

să fie egal cu Hașdeu împărțit

la c pătrat sau în funcție de lungimea

de undă Hash împărțit la c lambda

deoarece nu este egal cu Chaplin

Da de aici rezultă iarăși imediat

impulsuri impulsul unui Foton care

prin definiție este egal cu Mc

impulsul în general prin definiție

este mz dar deoarece fotonul în

vid are viteza si impulsul lui

va fi Mc din nou întruna materialul

oarecare omogen va fi Mc împărțit

la indicele de refracție sau el

va fi egal cu HP Lambda înlocuind

valoarea masei de mișcare din această

ecuație în fine deoarece radiațiile

electromagnetice nu interacționează

între ele două raze de lumină care

se intersectează Nu interacționează

nu vedem nu le vedem Spre exemplu

în doi induse sau trecând prin

orice fel de perturbație datorită

faptului că le sau întâlnit asta

înseamnă că nu interacționează

aceasta înseamnă că fotonul care

formează acele raze de lumină trebuie

să aibă sarcină 0 sarcină electrică

0 pentru că altfel ele ar interacționa

prin forță de tip coulomb acestea

sunt proprietățile fotonului care

râzi imediat direct din Definiția

lui acum să vedem cum anume Explică

această ipoteză cuantelor de energie

sub formă de fotoni efectul fotoelectric

când un Foton ce face parte din

radiația monocromatică ultravioletă

despre care am discutat în lei

trecută ciocănește un electron

de pe suprafața unui metal îi transferă

energia lui adică această energie

dacă această energie este mai mare

decât lucrul mecanic de extracție

atunci electronului este liberat

lucrul mecanic de extracție este

lucrul mecanic necesar pentru a

rupe acest electroni din structura

materialist din structura metal

El este acolo sub acțiunea sau

se află sub acțiunea unor forțe

de interacție de tip electromagnetic

și în concluzie avem nevoie să

efectuăm un lucru mecanic pentru

alt desprinde din acțiunea acestor

forțe și ale liberă Deci dacă el

este lucrul mecanic de extracție

atunci putem scrie imediat această

ecuație energia inițială a fotonului

Care este transferată electro se

va consuma în două feluri În primul

rând se va consuma În lucrul mecanic

de extracție În lucrul mecanic

de extracție ale electronului l

și în cazul în care electronul

după ce părăsește Metalul are o

viteză de se mișcă cu o viteză

nenulă se se află mișcarea Atunci

trebuie această energie cinetică

de mișcare trebuie să vină tot

din energia inițială a foto această

formulă simplă este formula Einstein

pentru efectul fotoelectric pentru

că după cum o vede imediat ea Explică

foarte simplu și elegant toate

cele 4 legi ale efectului fotoelectric

în acest tabel prezinți pentru

patru metale wolfram beriliu zinc

și cesiu valorile determinată experimental

ale acestui lucru mecanic de extracție

a unui electron în electroni volți

după cum am spus Haideți să vedem

cum anume ipoteza Frank și ecuația

sau formula Einstein pentru efectul

fotoelectric Explică legile experimentale

ale efectului fotoelectric prima

lege a efectului fotoelectric spune

că intensitatea foto curentului

de saturație este proporțională

cu fluxul radiației electromagnetice

când secvența A este constant aceasta

este formularea legi conform ipotezei

Einstein o radiație electromagnetică

este formată este un ansamblu de

fotoni ceea ce înseamnă pur și

simplu modul cel mai direct că

fluxul unei radiații electromagnetice

este dat de numărul de fotoni din

interiorul radiații asta înseamnă

că atunci când creștem fluxul radiației

prin această o săgeată în sus semnifică

parametrul dinainte crește Deci

când fluxul crește asta implică

Bineînțeles că numărul de fotoni

trebuie să crească dacă numărul

De fotoni ce cad pe metal crește

atunci numărul de fotoelectroni

Emil prin f fotoelectric va crește

iar dacă numărul de electroni crește

atunci bineînțeles curentul foto

curentul va crește în general și

în particular foto curentul de

saturație va crește Deci vedem

cum această asociere simplă radiații

electromagnetică egal ansamblu

de fotoni implică că cu foto curentul

de saturație trebuie să crească

cu flux radiații legea a doua stipulează

că energia cinetică maximă a fotoelectronilor

depinde de frecvență și nu depinde

de flux aceasta este cea de a doua

lege pe care am prezentat în lecția

trecută iarăși foarte simplu cea

de a doua formula Einstein scuzați

formula Einstein stipulează că

energia cinetică maximă acel mv

pătrat pe 2 este egal cu h n minus

el în concluzie energia cinetică

maximă depinde de frecvență și

nu depinde de fân depinde de numărul

de fotoni și de energia sau frecvența

lor iar își foarte o explicație

foarte simplă și direct cele trei

alegem spune că efectul fotoelectric

are loc atunci când frecvența radiației

depășește un prag o frecvență de

plug nu 0 care frecvență este caracteristică

metalului din această ecuație vedem

că efectul fotoelectric are loc

atunci când e si Max este mai mare

sau egal cu zero Adică are loc

atunci când electronii pot fi mii

având o energie cinetică cel puțin

dar în concluzie obține că efectul

fotoelectric are loc atunci când

h n este mai mare sau egal decât

el Deci efectul fotoelectric are

loc când nu este mai mare sau egal

decât un anume Nu 0 care devine

egal cu al împărțit la H Deci obținem

amândouă proprietățile că există

o frecvență de prag peste care

are loc efectul fotoelectric și

că această frecvență de prag este

raportul dintre lucrul mecanic

de extracție și Constanța universală

plan în concluzie va fi această

frecvență de prag o constantă de

material va avea o anumită valoare

pentru un anumit metal după cum

am văzut în minutele precedente

fiecare metal are o anumită valoare

fixă a acestuia și în fine ultima

lege stipula că timpul de emisie

este de ordinul secundelor Adică

foarte mic iarăși putem explica

foarte simplu deoarece interacțiunea

fotoni electron e aproape instantanee

are timp de timpul de interacțiune

dintre un Foton și electroni este

între adevăr de acest ordin de

magnitudine Deci întradevăr împrumut

foarte simplu și foarte elegant

toate legile experimentale al efectului

fotoelectric se explică prin ipoteza

Einstein în concluzie natura corpul

radiații electromagnetice se explică

după cum am spus simplu și elegant

Explică simplu și elegant legile

efectului fotoelectric și după

cum vom vedea La fel și ale efectului

compton această combinație între

ipotezele planck și Einstein Și

faptul că ele Explică două experimente

foarte importante fotoelectric

și contin au fost Punctul de plecare

al fizicii cuantice fizica cuantică

se referă la proprietatea sistemelor

fizice microscopice de a avea parametri

fundamentale energiei și așa mai

departe distribuiți nu continuu

și în poante Adică dacă vreți în

trepte sau în pași acesta este

termenul din fizică pentru o variație

discretă sau în trepte cuante Și

în fine există și aplicații practice

ale efectului fotoelectric și anume

celulele fotoelectrice detectoarele

de mișcare efectiv avem un cotor

Am și eu o Deci avem cat o dulce

a nodul a și avem un câmp și o

sursă o sursă de radiații electromagnetice

care produce un curent un foto

curent dacă un anumit obiect în

mișcarea lui întrerupe sursa de

radiații atunci acest foto curent

se va întrerupe Și el și detectorul

de mișcare sesizează întreruperea

surse de radiații același principiu

este folosit în unele detectoare

de fum și există și alte