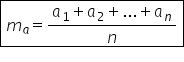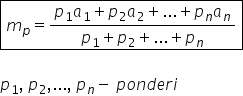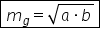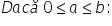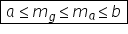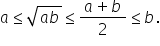Medii
Tag-uri
Partajeaza in Google Classroom

Transcript
media aritmetică și media geometrică
Voi începe cu media aritmetică
prin definiție media aritmetică
a numerelor reale x 1 x 2 puncte
puncte x n este X1 plus X2 plus
puncte puncte plus x n supra n
ne propunem să calculăm media aritmetică
a numerelor minus 1 supra 6 și
5 supra 6 media aritmetică a acestora
două numere va fi suma acestora
adică minus 1 supra 6 plus 5 supra
6 și totul supra 2 fiindcă sunt
două numere egal mai departe minus
1 supra 6 plus 5 supra 6 este egal
cu 4 supra 6 supra 2 știind că
linia de fracție înseamnă împărțire
și atunci vom scrie egal mai departe
cu 4 supra 6 împărțit la 2 egal
cu 4 supra 6 ori 1 supra 2 putem
să simplificăm pe diagonală cu
2 și obținem 2 supra 6 iar această
fracție se mai simplifică cu 2
și obținem 1 supra 3 Așadar media
aritmetică obținută este 1 supra
3 dacă avem trei numere se adună
toate numerele și se împarte la
trei atunci când avem mai multe
numere reale iar unele se repetă
adică apar de mai multe ori este
mai convenabil să calculăm media
aritmetică ponderată media aritmetică
ponderată va avea următoarea definiție
dacă X1 X2 puncte puncte xn sunt
numere reale iar pe 1 pe 2 pe an
sunt numere naturale care arată
numărul de repetări pentru X1 X2
puncte puncte x n atunci media
aritmetică ponderată este pe 1
x 1 plus pe 2 x 2 plus pe en Ericsson
supra pe 1 plus pe 2 plus puncte
puncte plus pe an numerele pe 1
pe 2 pe an se numesc ponderi de
propuneri să calculăm media ponderată
a numerelor radical din 18 Dar
de cal din 2 radical din 18 radical
din 18 și radical din doi pentru
a calcula media lor va folosi media
aritmetică ponderată ponderea numărului
radical din 18 este 3 fiindcă acest
număr apare de trei ori iar ponderea
numărului radical din 2 este 2
Inca chest număr se repetă de două
ori și atunci media ponderată va
fi egală cu 3 ori radical din 18
adică înmulțim fiecare număr cu
ponderea sa plus 2 ori radical
din 2 supra suma ponderilor adică
3 plus 2 egal mai departe vom scoate
factorii de sub radical descompunem
numărul 18 factori primi 18 împărțit
la 2 este 9 9 părți la 3 este 3
iar 3 împărțit la 3 este 1 și obținem
care Adi cal din 18 este 3 radical
din 2 continuăm aici egal cu 3
ori 3 radical din 2 plus 2 radical
din 2 supra 5 egal mai departe
3 ori 3 este 9 radical din 2 plus
2 radical din 2 supra 5 egal 9
plus 2 este 11 radical din 2 supra
5 în continuare să vedem Ce înțelegem
prin media geometrică Fie x un
număr rațional pozitiv diferit
de 0 și avem următoarea proporție
x supra 9 egal cu 4 supra x ne
propunem să calculăm valoarea lui
x din această relație având această
proporție vom folosi proprietatea
fundamentală a proporțiilor și
anume produsul mezilor este egal
cu produsul extremilor de aici
va rezulta că x ori x este egal
cu 9 ori 4 Dar exorex înseamnă
x la a doua și 9 ori 4 este 36
pentru a afla numărul x va trebui
să extragem rădăcina pătrată din
numărul 36 Așadar vom scrie că
x este egal cu radical din 36 fiind
un număr pozitiv radical din 36
va fi egal cu 6 spune că numărul
x este media geometrică a numerelor
9 și 4 Bogdan și definiția dacă
a și b sunt numere reale pozitive
atunci media geometrică care se
mai numește și proporțională se
calculează după formula radical
din a ori b între media aritmetică
și media geometrică a vem următoarea
relație numită inegalitatea mediilor
Fie a și b două numere reale pozitive
și presupunem că a este mai mic
sau egal decât b atunci a este
mai mic sau egal decât media geometrică
a numerelor a și b are la rândul
ei este mai mică sau egală decât
media aritmetică a numerelor și
mai mic sau egal decât b cele două
medii sunt cuprinse între cel mai
mic număr și cel mai mare număr
și mai mult media geometrică este
mai mică sau egală decât media
aritmetică media geometrică va
fi egală cu media aritmetică doar
dacă Numerele a și b sunt egale
Să facem un exemplu pentru a vedea
dacă se verifică această relație
Să presupunem că avem un număr
a egal cu doi și numărul b egal
cu 32 ne propunem să verificăm
această relație mai întâi vom calcula
media aritmetică a celor două numere
aceasta va fi egală cu 2 plus 32
supra 2 egal cu 34 supra 2 egal
cu 17 iar media geometrică a celor
două numere va fi radical din 2
ori 32 egal cu radical din 64 fiind
numere pozitive radical din 64
va fi egal cu 8 observăm din aceste
două relații că media geometrică
este mai mică decât media aritmetică
mai mult numărul 2 este mai mic
decât 8 8 este mai mic decât 17
și 17 este mai mic decât 32 și
atunci se verifica această relație
o să mai scriu o dată numărul a
este mai mic sau egal decât media
geometrică mai mic sau egal decât
media aritmetică a Care este mai
mică sau egală decât numărul b
în continuare o să facem două exerciții
primul exercițiu ne propunem să
calculăm media aritmetică a numerelor
x egal cu 3 radical din 3 minus
2 y egal cu 2 plus 3 radical din
3 media aritmetică a celor două
numere va fi suma lor x plus y
supra 2 egal acum Înlocuim pe x
cu 3 radical din 3 minus 2 și pe
y cu 2 plus 3 radical din 3 totul
supra 2 îi dau mai departe minus
2 plus 2 este 0 putem să îi tăiem
cu o linie oblică și rămâne 3 radical
din 3 plus 3 radical din 3 care
este egal cu 6 radical din 3 supra
2 putem să simplificăm 6 cu 2 6
împărțit la 2 este 3 și rezultatul
final va fi 3 radical din 3 al
doilea exercițiu la punctul a mic
se cere media geometrică a numerelor
radical din 2 și radical din 8
media geometrică a doua numere
este radical din produsul lor în
acest caz avem radical din radical
din 2 ori radical din 8 egal mai
departe radical din 2 ori radical
din 8 este radical din 16 egal
cu radical radical din 16 este
4 nicio obținem radical din 4 Care
este egal cu 2 iar la punctul b
se cere să calculăm media geometrică
a numerelor 36 radical din 2 și
radical din 2 supra 4 media geometrică
este radical din produsul celor
două numere adică 36 radical din
2 ori radical din 2 supra 4 egal
radical din 36 ori radical din
2 ori radical din 2 este radical
din 4 supra 4 egal radical din
36 ori radical din 4 este 2 supra
4 egal putem să simplificăm pe
diagonală cu 436 împărțit la 4
este 9 patru părți la 4 este 1
Deci obținem radical din 9 ori
2 egal în continuare cu radical
din 9 ori radical din 2 radical
din 9 știu că este 3 Deci rezultatul
final va fi 3 radical din 2