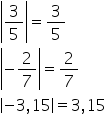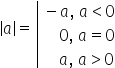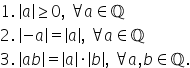Modulul unui număr rațional
Tag-uri
Partajeaza in Google Classroom
Transcript
valoarea absolută sau modulul unui
număr rațional este distanță măsurată
pe axa numerelor între origine
și punctul corespunzător numărului
rațional de exemplu valoarea absolută
a numărului 3 supra 2 va fi distanța
de la origine până la punctul a
și aceasta va fi egală cu 3 supra
2 scrie că modulul numărului 3
supra 2 este egal cu 3 supra 2
iar valoarea absolută a numărului
minus 3 supra 2 este lungimea segmentului
o a prim și aceasta este de asemenea
egală cu 3 supra 2 modulul numărului
minus 3 supra 2 este egal cu 3
supra 2 având în vedere că valoarea
absolută este o distanță iar va
fi întotdeauna un număr pozitiv
în general valoarea absolută a
unui număr rațional a este minus
A dacă A este negativ unde e prin
minus a înțelegem opusul numărului
a valoarea absolută este 0 dacă
a este egal cu 0 și valoarea absolută
a lui a este chiar A dacă A este
un număr pozitiv de exemplu valoarea
absolută a numărului minus 3 supra
2 va fi minus minus 3 supra 2 având
în vedere că a minus 3 supra 2
este negativ valoarea absolută
a se este minus minus 3 supra 2
și am văzut aceasta este egală
cu 3 supra 2 modulul numărului
zero este zero și modulul numărului
5 supra 6 este 5 supra 6 pentru
ca Acesta este un număr pozitiv
să vedem în continuare câteva proprietăți
ale modulului O primă proprietate
valoarea absolută a numărului a
este întotdeauna a mai mare sau
egal decât 0 Oricare ar fi a un
număr rațional mod la proprietate
modulul numărului minus a este
egal cu modulul numărului a Oricare
ar fi a un număr rațional am văzut
în primul exemplu că valoarea absolută
a lui minus 3 supra 2 este egală
cu valoarea absolută a lui 3 supra
2 și o altă proprietate valoarea
absolută a produsului a ori b este
egală cu valoarea absolută a numărului
a înmulțită cu valoarea absolută
a numărului b pentru oricare două
numere raționale a și b de exemplu
valoarea absolută a produsului
1 supra 2 ori 3 supra 5 este egală
cu valoarea absolută a numărului
1 supra 2 ori valoarea absolută
a numărului 3 supra 5 putem face
calculele în continuare și obținem
1 supra 2 ori 3 supra 5 egal cu
3 supra 10 să mai dăm câteva exemple
modulul numărului minus 3 supra
8 va fi minus minus 3 supra 8 și
egal cu 3 supra 8 Al doilea exemplu
valoarea absolută a numărului plus
2 supra 9 este egală cu 2 supra
9 modulul numărului minus 3 Putem
să scriem direct egal cu 3 iar modulul
numărului rațional 8 va fi egal
8
Valoarea absolută a unui număr raționalAscunde teorie X
Navigare în lectii
Cumpara abonament
