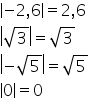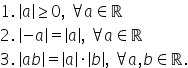Modulul unui număr real
Tag-uri
Partajeaza in Google Classroom
Transcript
valoarea absolută sau modulul unui
număr real este distanță măsurată
pe axa numerelor între origine
și punctul corespunzător numărului
real am reprezentat pe o axă patru
numere reale radical din 2 2 și
minus radical din 2 respectiv minus
2 valoarea absolută a numărului
radical din 2 va fi distanța de
la origine până la punctul a și
aceasta este egală cu radical din
2 valoarea absolută a numărului
2 este egală cu lungimea segmentului
OB Care este 2 valoarea absolută
sau modulul numărului minus radical
din 2 este distanța de la origine
până la punctul a prim fiind o
distanță aceasta este întotdeauna
pozitivă și egală cu radical din
2 iar valoarea absolută a lui minus
2 este lungimea segmentului o b
prim și aceasta este egală cu 2
să scrie ma chestie exemple Valoarea
absolută a lui radical din 2 este
radical din 2 valoarea absolută
a lui 2 este 2 valoarea absolută
a numărului minus radical din 2
este egală cu radical din 2 și
valoarea absolută a numărului minus
2 este egală cu 2 Observați că valoarea
absolută este întotdeauna un număr
pozitiv deoarece Ea este o distanță
Putem să scriem că valoarea absolută
a unui număr real a este minus
A dacă A este negativ 0 dacă a
este 0 și a dacă a este pozitiv
atunci când dorim să calculăm valoarea
absolută a unui număr negativ vom
schimba semnul numărului negativ
pentru a obține un număr pozitiv
de exemplu valoarea absolută a
numărului minus radical din 2 va
fi minus minus radical din 2 și
am văzut că aceasta este egală
cu radical din 2 valoarea absolută
a numărului zero va fi 0 iar în
cazul în care avem un număr real
pozitiv de exemplu valoarea absolută
a numărului radical din 3 aceasta
va fi egală cu radical din 3 să
mai facem un exemplu să calculăm
valoarea absolută a numărului 1
plus radical din 2 aici avem un
număr pozitiv pentru că radical
din 2 este aproximativ egale cu
1 iar unul adunat cu 1 este 2 așa
Dar acest număr este pozitiv și
atunci valoarea absolută Asta va
fi egală cu 1 plus radical din
2 acest număr este mai mare decât
0 și un alt exemplu să calculăm
valoarea absolută a numărului 1
minus radical din 2 noi calcula
alăturată această diferență 1 minus
radical din 2 va fi egal cu 1 minus
îl aproximam pe radical din 2 cu
1 1 minus 1 este minus 0 observăm
Așadar că numărul scris în modul
este mai mic decât 0 în cazul în
care numărul este mai mic decât
0 se schimbă semnul acelui număr
pentru a obține o valoare pozitivă
în acest caz om scrie că valoarea
absolută a lui 1 minus radical
din 2 este minus paranteză 1 minus
radical din 2 după regula aceasta
modul de a este minus A dacă A
este negativ iar în cazul nostru
a este numărul 1 minus radical
din 2 semnul minus în fața unei
paranteze schimbă semnele numerelor
din paranteză și obținem minus
1 plus radical din 2 care se mai
poate scrie egal în continuare
cu radical din 2 minus 1 atenția
și a Dar când trebuie să calculați
valoarea absolută a unui număr
să Verificați întotdeauna dacă
numărul acela este pozitiv sau
negativ în cazul în care este negativ
trebuie să punem semnul minus în
fața numărului pentru a obține
un număr pozitiv să vedem câteva
proprietăți ale modulului modulul
unui număr real a este întotdeauna
mai mare sau egal decât 0 și pentru
orice număr real a are loc egalitatea
valoarea absolută a lui minus a
este egală cu valoarea absolută
a lui a am văzut în primul exemplu
că valoarea absolută a lui minus
radical din 2 este egală cu valoarea
absolută a lui radical din 2
Valoarea absolută a unui număr realAscunde teorie X
Navigare în lectii
Cumpara abonament
