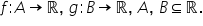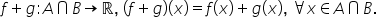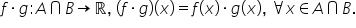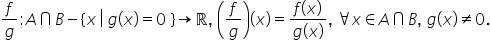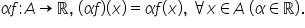Operații cu funcții numerice

în acest video o să definim câteva

operații cu funcții numerice dar

mai întâi aș vrea să vedem Ce înțelegem

prin funcții egale și o să încep

cu un exemplu simplu Fie e f și

g două funcții definite pe mulțimea

zero doi cu valori în R f d x este

egal cu x iar g de x este egal

cu x pătrat supra 2 Haideți să

calculăm valorile acestor funcții

în fiecare punct f de 0 este egal

cu 0 G de 0 este egal cu 0 la pătrat

supra doi egal cu 0 observăm Așadar

că f de 0 este egal cu g d 0 calculăm

și F de 2 f de 2 este egal cu 2

și g de 2 este egal cu 2 la a doua

pe 2 adică 2 prin urmare f de 2

este egal cu g de 2 observăm Așadar

că valorile funcțiilor f și g sunt

egale pentru fiecare punct din

domeniul de definiție cu alte cuvinte

putem să scriem că f de x este

egal cu g de x oricare ar fi x

un punct din domeniul de definiție

dacă ne uităm puțin la aceste funcții

observăm că ele au același domeniu

de definiție Iată mulțimea zero

doi au același cod domeniu și punctul

al funcțiile coincide astfel de

funcție se vor numi funcție Gal

și vopsi rie egal cu g observăm

că nu este obligatoriu ca cele

două funcții să aibă aceeași lege

de corespondență Iată f de x este

egal cu x iar g de x este x pătrat

supra 2 cu toate acestea funcțiile

au aceeași valoare pentru fiecare

punct din domeniul de definiție

Așadar vom scrie că e f e este

egal cu g și acum să definim o

primă operație cu funcții numerice

vă reamintesc că funcțiile numerice

sunt funcții definite pe mulțimea

numerelor reale sau pe submulțimi

ale mulțimii numerelor reale funcțiile

numerice se mai numesc și funcții

reale de variabile reale o prima

operație despre care aș vrea să

discutăm este suma a două funcții

numerice fie f o funcție definită

pe o mulțime oarecare a cu valori

în r iar g o funcție definită pe

d cu valori in R unde a și b sunt

submulțimi ale mulțimii numerelor

reale atunci suma funcțiilor F

și G este funcția notată astfel

f plus gem domeniul maxim de definiție

al acestei funcții este intersecția

domeniilor de definiție a funcțiilor

F și G Așadar f plus G este o funcție

definită pe a intersectat cu b

cu valori în R dată prin legea

S Plus g de x egal cu f de x plus

g de x oricare ar fi x un punct

din a intersectat cu b cu alte

cuvinte Suma a două funcții un

punct este egală cu suma valorilor

funcțiilor în acel punct să luăm

și un exemplu și e f definită pe

r cu valori în R f de x egal cu

2x plus 5 și g definită pe r cu

valori in r g de x egal cu 2 minus

x atunci ies plus G este o funcție

definită pe r cu valori in R din

moment ce e f și g au același domeniu

de definiție evident și domeniul

de definiție a sumei va fi tot

r iar f plus G de x va fi egal

cu F d x plus GTX și egal cu 2

x plus 5 plus 2 minus x egal cu

x plus 7 Iată Am calculat suma

funcțiilor f și g și acum să trecem

la o altă operație Produsul a două

funcții f și g Considerăm funcția

f definită pe a cu valori in R

și g definită pe b cu valori in

R unde a și b sunt submulțimi ale

mulțimii numerelor reale atunci

produsul funcțiilor F și G este

funcția notată cu EF urgent aceasta

se definește pe a intersectat cu

b cu valori în R iPhone GTX va

fi egal cu F d x ori GTX Deci Produsul

a două funcții întru un punct este

egal cu produsul valorilor funcțiilor

în acel punct de exemplu dacă avem

aceleași funcții f definită pe

r cu valori în R f de x egal cu

2x plus 5 și g definită pe r cu

valori în R g de x egal cu 2 minus

x atunci produsul funcțiilor F

și G este funcția f definită pe

r cu valori in r f g d x ma fie

egal cu f de x ori GTX fdx în cazul

acesta este 2x plus 5 iar g de

x este 2 minus x facem calculele

obținem 4 x minus 2x pătrat plus

10 minus 5x egal cu minus 2x pătrat

minus x plus 10 în cazul în care

funcțiile f și g nu ar fi avut

același domeniu de definiție atunci

domeniul maxim de definiție al

produsului ar fi fost intersecție

a domeniilor de definiție ale celor

două funcții o altă operație despre

care o să discutăm este câtul la

două funcții fie f definită pe

a cu valori in r g definită pe

d cu valori in r a și b submulțimi

ale lui R Câtul a două funcții

F și G este funcția notată f pe

G aceasta se definește pe a intersectat

cu b de la atenție trebuie să scoatem

din acest domeniu de definiție

acele valori pentru care se anulează

numitorul de scădem mulțimea acelor

puncte x în care g de x este egal

cu 0 și cu valori în R f supra

g de x este egal cu f de x supra

g de x De exemplu dacă funcția

f de x este egală cu 2 x plus 5

iar g de x este 2 minus x atunci

x supra g de x este egal cu 2 x

plus 5 supra 2 minus x observăm

că numitorul la chestie fracții

se anulează pentru x egal cu 2

prin urmare funcția f supra G este

definită pe R din care eliminăm

numărul 2 și cu valori în aer Așadar

pentru Câtul a două funcții trebuie

să avem grijă să eliminăm din domeniul

de definiție acele valori care

anulează numitorul o altă operație

despre care o să discutăm este

produsul dintre o funcție și un

număr real dacă avem funcția f

definită pe apă valori in R și

Alfa un număr real atunci funcția

Alfa f pe a cu valori in R Unde

f de x este egal cu alfa ori RDX

acestea au fost principalele operații

cu funcții în continuare Aș vrea

să facem două observații oprim

observație în cazul în care avem

n funcții F1 F2 și așa mai departe

f n definite pe a cu valori in

R atunci suma acestor funcții este

funcția notată F1 plus F2 plus

și așa mai departe plus f n aceasta

se definește pe a cu valori in

R dar F1 plus S2 Plus sin2x va

fi egal cu F 1 de x plus 2 x plus

și așa mai departe plus f&d x oricare

ar fi x din domeniul de definiție

Așadar suma funcțiilor întru un

punct este egală cu suma valorilor

funcțiilor în acel punct iar produsul

F1 F2 ori și așa mai departe ori

sin2x va fi egal cu F 1 de x ori

f2d x ori puncte puncte ori f de

x în cazul în care funcțiile sunt

egale dacă F1 este egal cu F2 egal

cu F n și egal cu F atunci suma

acestor an funcții F 1 plus 2 plus

FM dx va fi egal cu n ori fdx pentru

că avem n funcții egale iar produsul

F1 ori F2 s&d x este egal cu a

la puterea m d x și egal cu f de

x totul la puterea n și o ultimă

observație dacă avem două funcții

f definită pe a cu valori in r

g definită pe d cu valori in R

unde a și b sunt submulțimi ale

mulțimii numerelor reale atunci

vom defini diferența dintre funcțiile

f și g ca fiind funcția notată

f minus G aceasta e definită pe

a intersectat cu b cu valori in

r f minus g de x este egal cu f

de x minus gdx această operație

ca și observație pentru că ea este

de fapt o consecință a operațiilor

amintite mai devreme pentru că

f minus gem este de fapt e adunat

cu minus G deci practic avem aici

o sumă iar minus G este de fapt

minus Orange produsul dintre numărul

real minus 1 și funcția G De exemplu

dacă f de x este 2 x plus 5 și

g de x este 2 minus x ambele funcții

definite pe r cu valori in R atunci

EF minus g de x este egal cu 2

x plus 5 minus 2 minus x egal cu

3 x plus 3 adunarea funcțiilor

numerice ale câteva proprietăți

Ce rezultă din proprietățile adunării

numerelor reale să nu uităm că

funcțiile numerice sunt funcții

definite pe r sau pe submulțimi

ale mulțimii numerelor reale Așadar

adunarea funcțiilor este asociativă

comutativă iar funcția nulă este

element neutru pentru adunare funcția

nulă este funcția care are valoarea

0 fiecare punct oricare ar fi x

un punct din domeniul de definiție

apoi înmulțirea funcțiilor este

de asemenea asociativă comutativă

iar funcția unitate este element

neutru pentru înmulțire funcția

unitate este funcția care are valoarea

1 pentru orice punct din domeniul

de definiție iar înmulțirea funcțiilor

este o operație distributivă față

de adunare f pe lângă G Plus h

este egal cu F G Plus f e h