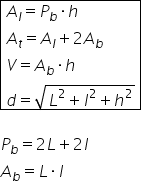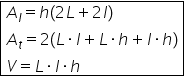Paralelipipedul dreptunghic (formule)

în această secvență vom vedea Care

sunt formulele uzuale pentru paralelipipedul

dreptunghic știind deja că acest

corp geometric este un caz particular

de prismă dreaptă și să trecem

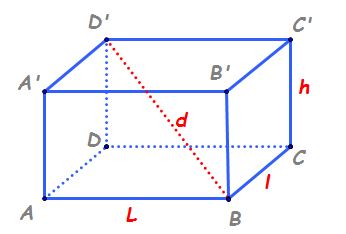
și dimensiunile avem aici lungimea

care se regăsește și aici e aici

și aici și avem aici lățimea care

se regăsește și ea Evident ca Scrisul

și aici și aici și aici Și avem

și aici înălțimea mai întâi vom

începe cu Găsirea ariei laterale

unui paralelipiped dreptunghic

aria laterală reprezintă suma ariilor

fețelor laterale cu alte cuvinte

avem aici un dreptunghi care este

congruent cu cel din spate are

aceleași dimensiuni și acest dreptunghi

este congruent cu acesta din stânga

Prin urmare avem două perechi de

Drept unghiuri congruente Deci

vom avea aria acestui dreptunghi

este lungimea ori înălțime Deci

avem doi ori lungime ori înălțime

a adunat cu de două ori aria acestui

dreptunghi adică lățime ori înălțime

sau putem să rescriem această formulă

astfel putem să dăm factor comun

pe H sigur putem să dăm și pe doi

însă o să vedeți De ce nu îl dăm

Deci avem H pe lângă 2 ori el a

adunat cu 2 ori el mic din această

scriere Ce obținem aici în paranteză

Păi de două ori lungimea Iată adunată

cu de două ori lățimea obținem

de fapt perimetrul bazei deci putem

să notăm că aria laterală formula

se scrie perimetrul bazei înmulțit

cu înălțimea iar dacă vorbim De

fapt aceeași formulă pe care am

regăsit o pentru aria laterală

și la prismă triunghiulară regulată

formula pentru aria totală este

suma ariilor tuturor fețelor prismei

adică în cazul nostru a paralelipipedului

dreptunghic toate fețele sunt dreptunghiuri

Deci avem aria laterală adunată

cu de două ori aria bazelor Cât

este aria unei baze aria bazei

este egală cu avem un dreptunghi

lungimea o lățime formula volumului

pentru un paralelipiped dreptunghic

este aceeași cu formula pe care

am folosit o la Prisma triunghiulară

regulată și anume aria bazei ori

înălțimea de fapt pentru orice

prisma dreaptă volumul se calculează

Înmulțind aria bazei cu înălțimea

și mai putem să scriem această

formulă astfel o parte Larisa pentru

acest corp geometric și anume aria

bazei este lungime ori lățime înmulțită

cu înălțimea parte ca să determinăm

volumul unui paralelipiped dreptunghic

vom înmulțit cele trei dimensiuni

idee să încadrăm câteva formule

am încadrat pentru formula pentru

aria laterală formula pentru aria

totală este aceasta și formula

volumului formulele pe care le

am încadrat sunt valabile Atenție

pentru orice prismă dreaptă fie

că vorbim de prismă triunghiulară

regulată sau de paralelipiped dreptunghic

să determinăm acum lungimea diagonalei

unui paralelipiped dreptunghic

acest corp geometric are patru

diagonale congruente și palme Alege

una dintre ele de exemplu a prim

c și o voi nota cu d mic de la

diagonală și vrem să determinăm

lungimea acestei diagonale Păi

ce fel de triunghi este triunghiul

a prim a c pentru că Folosind un

de acest triunghi vom determina

lungimea diagonalei Iată avem aici

a prim a perpendiculară pe planul

bazei ABCD AC este inclusă în acest

plan înseamnă că a prim a e perpendiculară

și pe ei si deci putem să trecem

că avem aici un unghi de 90 de

grade Să notăm ce am zis a prim

a perpendiculară pe planul bazei

ABC AC este inclusă în planul ABC

de unde rezultă că a prim a e perpendiculară

pe ace foarte cuvinte avem triunghiul

a prim a c care are măsura unghiului

A de 90 de grade diagonala adică

segmentul a prim c este ipotenuză

în triunghiul a prim AC Deci aplicăm

teorema lui Pitagora rezultă din

teorema lui Pitagora că lungimea

segmentului a prim c la pătrat

este egală cu a 1-a la pătrat adunată

cu acela pătrat și acum trebuie

să găsim lungimile acestor catete

a prim a este egală cu a c Cu cât

este egală Păi iată că în triunghiul

ABC avem că măsura unghiului B

este de 90 de grade înseamnă că

putem să aplicăm în acest triunghi

teorema lui Pitagora prin urmare

În triunghiul a b c cu măsura unghiului

b de 90 de grade rezultă tot din

teorema lui Pitagora că acela pătrat

este egală cu AB la pătrat plus

bc la pătrat adică cu l mare la

pătrat adunat cu l mic la pătrat

Ce facem acum vom înlocui aici

deci a prim c am notat o cu de

la pătrat este egală cu a prim

a adică H la pătrat adunat cu ace

la pătrat ia de este egală cu această

sumă adică el mare la a doua plus

l mic la a doua și atât că am găsit

și formula diagonalei unui paralelipiped

dreptunghic diagonală A lungimea

diagonalei ridicate la pătrat este

egală cu mare la a doua plus l

mic la a doua plus H la a doua

sau dacă vreți Putem să scriem

că Diagonala este egală cu trecem

totul sub radical și vom avea așa

el mare la pătrat adunat cu l mic

la pătrat plus hashmi la pătrat

totul sub radical aceasta este

formula pentru determinarea diagonalei

unui paralelipiped dreptunghic