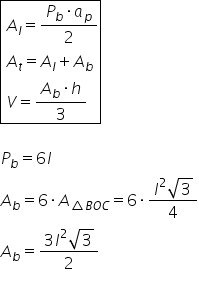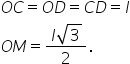Piramida hexagonală regulată (formule)

în diferite manuale sau culegeri

puteți să întâlniți și probleme

legate de piramida hexagonală regulată

așa că Haide să discutăm puțin

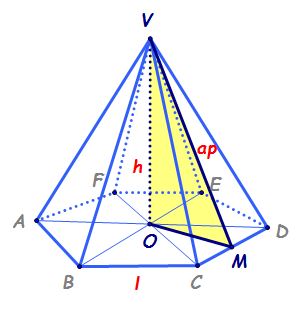
despre o asemenea piramidă Dacă

ea se numește hexagonală regulată

înseamnă că baza este un hexagon

regulat și muchiile laterale sunt

congruente Deci avem îndeplinite

aceste două lucruri când vorbim

de o piramidă hexagonală regulată

dacă muchiile laterale sunt congruente

înseamnă că fețele laterale Ce

reprezintă ele sunt niște triunghiuri

și ele sunt de fapt triunghiuri

isoscele congruente Deci v a b

v b c și așa mai departe sunt toate

triunghiul isoscel a concurente

baza este hexagon regulat Să ne

amintim Ce înțelegem prin hexagon

regulat avem un poligon care are

șase laturi paturile sunt congruente

la fel și unghiurile sunt congruente

Deci măsura unghiului a egală cu

măsura unghiului b cu măsura unghiului

c și așa mai departe fiecare unghi

are măsura de 120 de grade înălțimea

între o piramidă hexagonală regulată

este segmentul care unește vârful

piramidei cu centrul cercului circumscris

bazei centrul acestui cerc se află

la intersecția diagonalelor hexagonului

regulat care se află la baza Acestea

fiind spuse să găsim acum formulele

pentru o piramidă hexagonală regulată

În primul rând aria laterală este

suma ariilor fețelor laterale ca

fețe laterale avem șase triunghiuri

isoscele congruente Deci pumnul

Da 6 mult cu aria unui triunghi

de exemplu aria triunghiului pe

care să îl alegem b c d Cum exprimăm

aria triunghiului V a c d și dacă

ducem înălțimea corespunzătoare

laturii CD ca să facem acest lucru

putem să construim mijlocul segmentului

CD să notăm cu m v ă m este mediană

în triunghiul isoscel b c d cu

a c este congruent cu bd înseamnă

că avem aici un unghi de 90 de

grade adică b m este perpendiculară

pe CD cu alte cuvinte aria triunghiului

bcd este egală cu cd înmulțit cu

vm care atenție reprezintă apotema

piramidei Deci ori apotema piramidei

supra 2 Și acum înlocuim Deci avem

această relație Chiar o să le trec

pe amândouă către stânga rezultă

aria laterală este egală cu 6 înmulțit

cu în loc de aria acestui triunghi

notăm acest raport adică avem ce

de înmulțit cu apotema piramidei

supra doi nu vom face acum această

simplificare 6 și 2 prin 2 și o

să înmulțim pe 6 cu lungimea segmentului

CD știind că baza este un hexagon

regulat de toate laturile au lungimea

egală cu lungimea segmentului si

de asta înseamnă că dacă adunăm

de șase ori această lungime vom

obține chiar perimetrul bazei Deci

rezultă că aria laterală are următoarea

formulă perimetrul bazei înmulțiri

cu apotema piramidei supra 2 cred

că deja bati învățat cu această

formulă iar ceea și ca la piramida

triunghiulară și patrulateră regulată

aria totală este egală cu De fapt

chiar să o trecem alături aria

totală este suma dintre aria laterală

și aria bazei Cât este aria bazei

poate cuvinte vrem să notăm aria

unui hexagon regulat știm deja

că hexagonul regulat este alcătuit

să zicem așa din șase triunghiuri

echilaterale congruente Iată e

f o acest triunghi este un triunghi

echilateral și este congruent cu

a o b b o c c o d d o e și e o

f Deci e destul de simplu să găsim

aria unui hexagon regulat avem

șase triunghiuri echilaterale congruente

Deci notăm 6 înmulțiri cu aria

unui triunghi echilateral dacă

trecem aici cu notăm cu l mic latura

triunghiului echilateral vom avea

Așa șase înmulțit cu trecem aria

triunghiului echilateral l la a

doua radical din 3 supra 4 sigur

putem mai să facem următoarea simplificare

6 și 4 simplificăm prin 2 și vom

obține trei ori el la a doua radical

din 3 supra 2 dacă vrem putem să

reținem această formulă dacă nu

putem oricând să o ducem pentru

că știm avem de șase ori aria unui

triunghi echilateral formula pentru

volum este aceeași ca la celelalte

piramide aria bazei ori înălțimea

supra 3 unde înălțime este reprezentată

de pe segmentul V tot ca exercițiu

să găsim acum apotema bazei cu

alte cuvinte Apotema hexagonului

regulat Adică o m segmentul o m

este perpendicular pe cd deci putem

să trecem aici ca avem un unghi

de 90 de grade nu știu cât de bine

o să se înțeleagă om este de fapt

înălțime în triunghi echilateral

c o d cu alte cuvinte apotema bazei

adică om este egală cu știm deja

formula pentru înălțimea unui triunghi

echilateral latura radical din

3 supra 2 acestea au fost formulele

pentru piramida hexagonală regulată

foarte ușor să observăm că aria

laterală Iată are aceeași formulă

pe care am întâlnit o și la piramida

triunghiulară regulată și la cea

patrulateră regulată la fel și

formula pentru aria totală formula

pentru volum cu alte cuvinte Toate

aceste formule sunt destul de ușor

de reținut